transformer多头自注意力

transformer多头自注意力

参考：《手动学深度学习》https://zh.d2l.ai/chapter_attention-mechanisms/multihead-attention.html

1.1 缩放点积注意力

示意图如下：

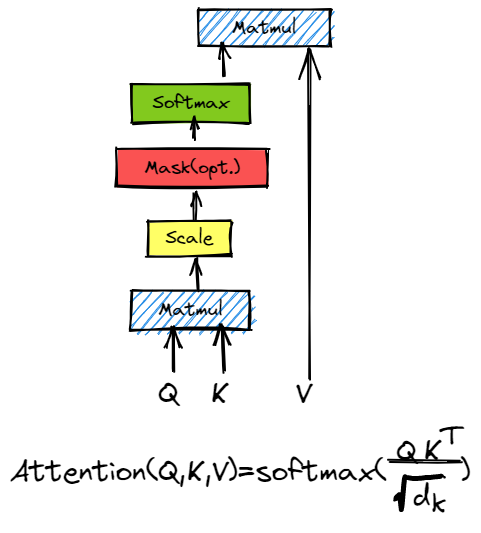
缩放点积注意力的公式是

\[\mathrm{softmax}\left(\frac{\mathbf Q \mathbf K^\top }{\sqrt{d}}\right) \mathbf V \in \mathbb{R}^{n\times v} \]

各矩阵的维度为：

B: 批量大小
M: key和value的个数
N: query的个数
d: 维度（即查询/键的维度）

Q: (B,N,d)
K: (B,M,d)
V: (B,M,dv)

缩放是为了保证softmax值合理，不至于内积后数字过大或过小，而导致softmax值出现接近于1和0的情况。

例如：

x = [0.5, -1, 2]
softmax(x)  : [0.1753, 0.0391, 0.7856] # better
softmax(2*x): [0.0473, 0.0024, 0.9503] 

这里解释一下各个矩阵的含义，\(\mathbf{Q}\)为查询向量，\(\mathbf{K}\)和\(\mathbf{V}\)分别存储的是键和值

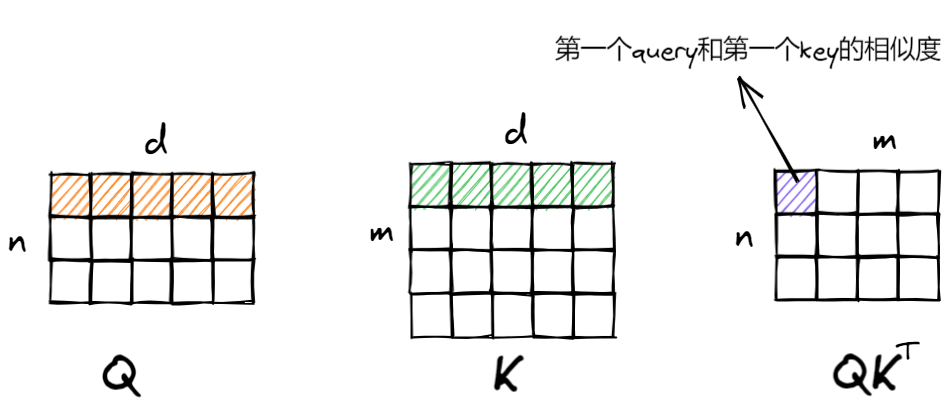
因为\(\mathbf{Q}\)、\(\mathbf{K}\)要通过点积计算相似度，所以\(\mathbf{Q}\)、\(\mathbf{K}\)具有相同的维度（为了简便可以让三者维度都相同）。同时，\(\mathbf{K}\)和\(\mathbf{V}\)具有相同的个数（一个key对应一个value）。例如：n个query，m个key和value，则\(\mathbf{QK}^{\mathrm{T}}\)[1,2,5]代表第1个batch第2个query和第5个key的点积（相似度）。

\(\mathbf{QK}^{\mathrm{T}}\mathbf{V}\)的含义为，通过n个query计算和m个value所对应key的相似度，并对value进行加权，从而得到n个加权后的向量，向量维度和value相同。如\(\mathbf{QK}^{\mathrm{T}}\mathbf{V} \)[1,3,:]代表第1个batch第3个query得到的向量。

1.2 遮蔽注意力权重

为了仅将有意义的词元作为值来获取注意力汇聚，在计算\(\mathbf{QK}^{\mathrm{T}}\mathbf{V}\)之前，我们需要对进\(\mathbf{QK}^{\mathrm{T}}\)行处理，因为数据中可能会含有填充的词元<pad>，而这些词元是不应该被“注意到”的，也就不需要加权对应的value。

下面我们对mask进行演示，假设我们的数据为：

i  love    you   <pad>
i  can't   go    there
of course  <pad> <pad>

我们可以看到数据的有效长度为3、4、2。

回想一下1.1中\(\mathbf{QK}^{\mathrm{T}}\)的含义，我们知道，行对应着query，而列对应着query和key的相似度，下图灰色部分就是需要mask的地方。

我们可以指定一个有效序列长度valid_lens（即词元的个数）， 以便在计算softmax时过滤掉超出指定范围的位置。例如，我们可以在下面的sequence_mask函数中，将任何超出有效长度的位置（如上图灰色部分）设置为一个很大负值，以便计算softmax时将其过滤。

def sequence_mask(X: torch.Tensor, lens: torch.Tensor, mask_value=0) -> torch.Tensor:
    """
    对X最后一个维度进行mask

    :param X: n-d
    :param lens: 1-d or n-d
    :param mask_value: mask value
    :return: n-d masked sequence
    """
    # reshape X to 2-d
    X_2d = X.reshape(-1, X.size(-1))
    # reshape lens to column vector
    lens = lens.reshape(-1, 1)

    # broadcast (1,n) < (m,1) = (m,n)
    mask = torch.arange(X_2d.size(-1))[None, :] >= lens

    # reshape 2-d to X
    X_2d[mask] = mask_value
    # return origin shape
    return X

为了演示该函数，我们定义一个形状为（1，2，4）的随机整数矩阵，并使用lens矩阵作为有效长度进行mask。

y = torch.randint(1, 8, (1, 2, 4)) # random vector
print(y)
lens = tensor([1, 2]) # valid_lens
r = sequence_mask(y, lens, mask_value=-1e3) # mask -1e3
print(r)
print(nn.functional.softmax(r.to(torch.float32),dim=-1)) # softmax

tensor([[[7, 5, 5, 4],
         [3, 7, 7, 7]]])
tensor([[[    7, -1000, -1000, -1000],
         [    3,     7, -1000, -1000]]])
tensor([[[1.0000, 0.0000, 0.0000, 0.0000],
         [0.0180, 0.9820, 0.0000, 0.0000]]])

至此，我们可以编写一个DotProductAttention类，来计算缩放点积注意力。这里对注意力权重\(\mathbf{QK}^{\mathrm{T}}\)使用了dropout。

#@save
class DotProductAttention(nn.Module):
    def __init__(self, dropout):
        super(DotProductAttention, self).__init__()
        self.dropout = nn.Dropout(dropout)

    def forward(self, Q: torch.Tensor, K: torch.Tensor, V: torch.Tensor, valid_lens: Optional[torch.Tensor] = None):
        """
        B: 批量大小\n
        M: key和value的个数\n
        N: query的个数\n
        d: 维度\n

        :param Q: (B,N,d)
        :param K: (B,M,d)
        :param V: (B,M,dv)
        :param valid_lens: 1-d or n-d
        """
        # Q的维度
        d = Q.size(-1)
        # (B,N,d) @ (B,d,M) = (B,N,M) 计算出每一个query与每一个key的相似度
        scores = Q @ K.transpose(1, 2) / math.sqrt(d)
        # 进行mask
        masked_scores = sequence_mask(scores, valid_lens)
        # 对最后一个维度计算softmax
        self.attention_weights = nn.functional.softmax(masked_scores,dim=-1)
        # (B,N,M) @ (B,M,dv) = (B,N,dv) 通过相似度加权value，形成N个(query个数)向量
        return self.dropout(self.attention_weights) @ V

1.3 多头自注意力

多头自注意力的示意图如下：

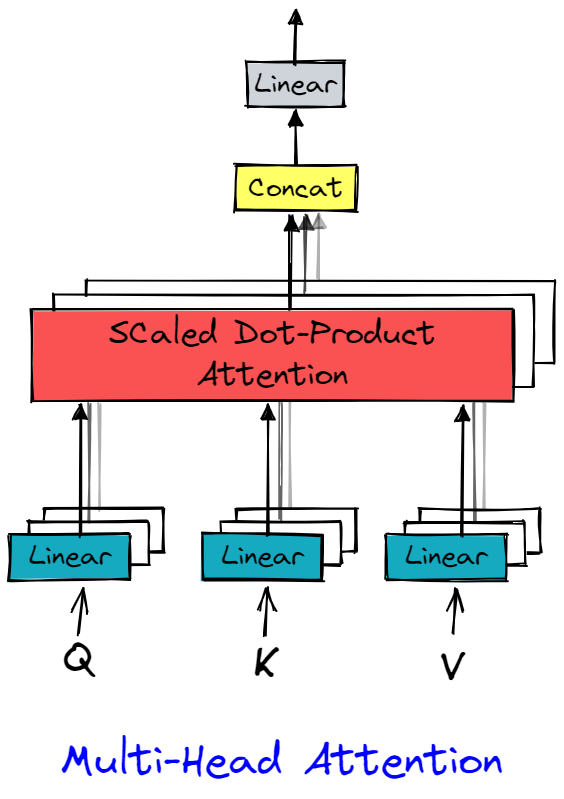
概念这里不再细说，本质上就是通过线性变换，产生\(h\)组不同的\(\mathbf{Q}\)、\(\mathbf{K}\)和\(\mathbf{V}\)（如\(\mathbf{X}\)分别进行线性变换\(\mathbf{W}_{1}^{\left( q \right)}\)、\(\mathbf{W}_{1}^{\left( k \right)}\)、\(\mathbf{W}_{1}^{\left( v \right)}\)，从而得到\(\mathbf{Q}_1\)、\(\mathbf{K}_1\)、\(\mathbf{V}_1\)），分别计算注意力汇聚的结果\(\mathbf{QK}^{\mathrm{T}}\mathbf{V}\)并拼接在一起，最后经过一个线性变换\(\mathbf{W}_{o}\)得到最后的输出。

需要注意的是，为了并行计算，我们让每个查询、键、值各自的个数相同（\(\mathbf{Q}\)和\(\mathbf{Q}\)相同，\(\mathbf{K}\)和\(\mathbf{K}\)相同，\(\mathbf{V}\)和\(\mathbf{V}\)相同），即拼成一个长方形。进一步简便，我们可以让\(\mathbf{Q}\)、\(\mathbf{K}\)、\(\mathbf{V}\)的维度也相同，均为n_hiddens / h，加起来刚好为n_hiddens（相当于\(h\)个线性变换将\(\mathbf{X}\)投影到均等的\(h\)小份）。示意图如下所示：

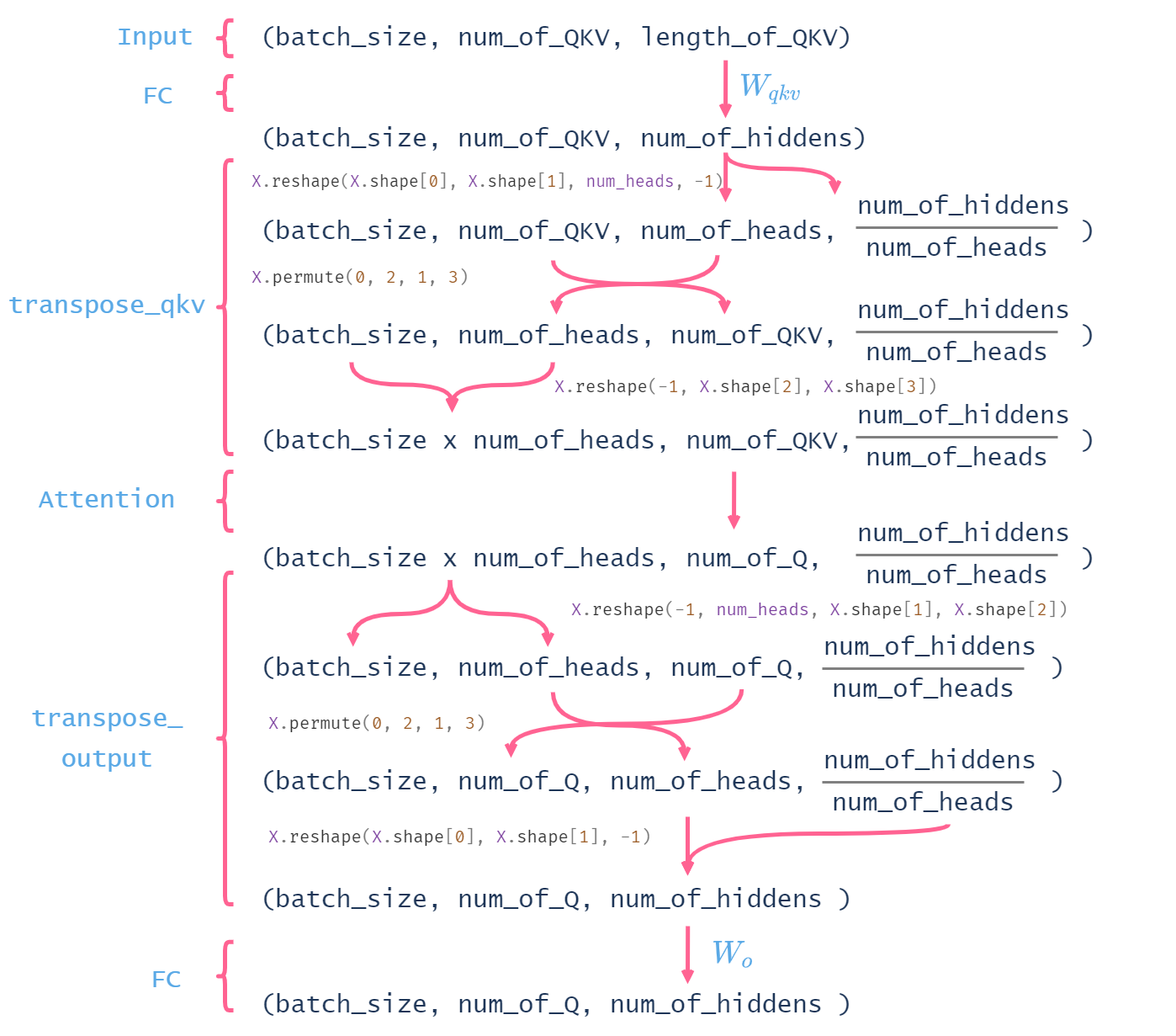
接下来，为了将计算好的\(\mathbf{Q}\)、\(\mathbf{K}\)、\(\mathbf{V}\)放入DotProductAttention进行计算，我们通过下面的方法对\(\mathbf{Q}\)、\(\mathbf{K}\)、\(\mathbf{V}\)进行形状转换：

def transpose_qkv(X, num_heads):
    X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)
    X = X.permute(0, 2, 1, 3)
    return X.reshape(-1, X.shape[2], X.shape[3])


def transpose_output(X, num_heads):
    X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])
    X = X.permute(0, 2, 1, 3)
    return X.reshape(X.shape[0], X.shape[1], -1)

示意图如下所示：

综上，我们编写一个多头注意力类，代码如下：

class MultiHeadAttention(nn.Module):
    def __init__(self, num_hiddens,num_heads, dropout):
        super(MultiHeadAttention, self).__init__()
        self.num_heads = num_heads
        self.attention = DotProductAttention(dropout)
        self.W_q = nn.Linear(num_hiddens, num_hiddens, bias=False)
        self.W_k = nn.Linear(num_hiddens, num_hiddens, bias=False)
        self.W_v = nn.Linear(num_hiddens, num_hiddens, bias=False)
        self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=False)

    def forward(self, queries, keys, values, valid_lens):
     
        queries = transpose_qkv(self.W_q(queries), self.num_heads)
        keys = transpose_qkv(self.W_k(keys), self.num_heads)
        values = transpose_qkv(self.W_v(values), self.num_heads)

        if valid_lens is not None:
            # 在轴0，将第一项（标量或者矢量）复制num_heads次，
            # 然后如此复制第二项，然后诸如此类。
            valid_lens = torch.repeat_interleave(
                valid_lens, repeats=self.num_heads, dim=0)
        
        output = self.attention(queries, keys, values, valid_lens)

        output_concat = transpose_output(output, self.num_heads)
        return self.W_o(output_concat)