BUAA OO 第三单元总结

🖊概述

本单元作业的目的是完成一个社交关系的模拟程序。在此社交关系被抽象成三个对象：Network, Group, Person；Person和Person/Group之间还可以发送各种Message。我们需要根据JML来完成一些指令，以完成题目的要求，如查询组内的社交值之类的操作。本单元的完成需要用到一些图论的基础算法。

🗺架构设计

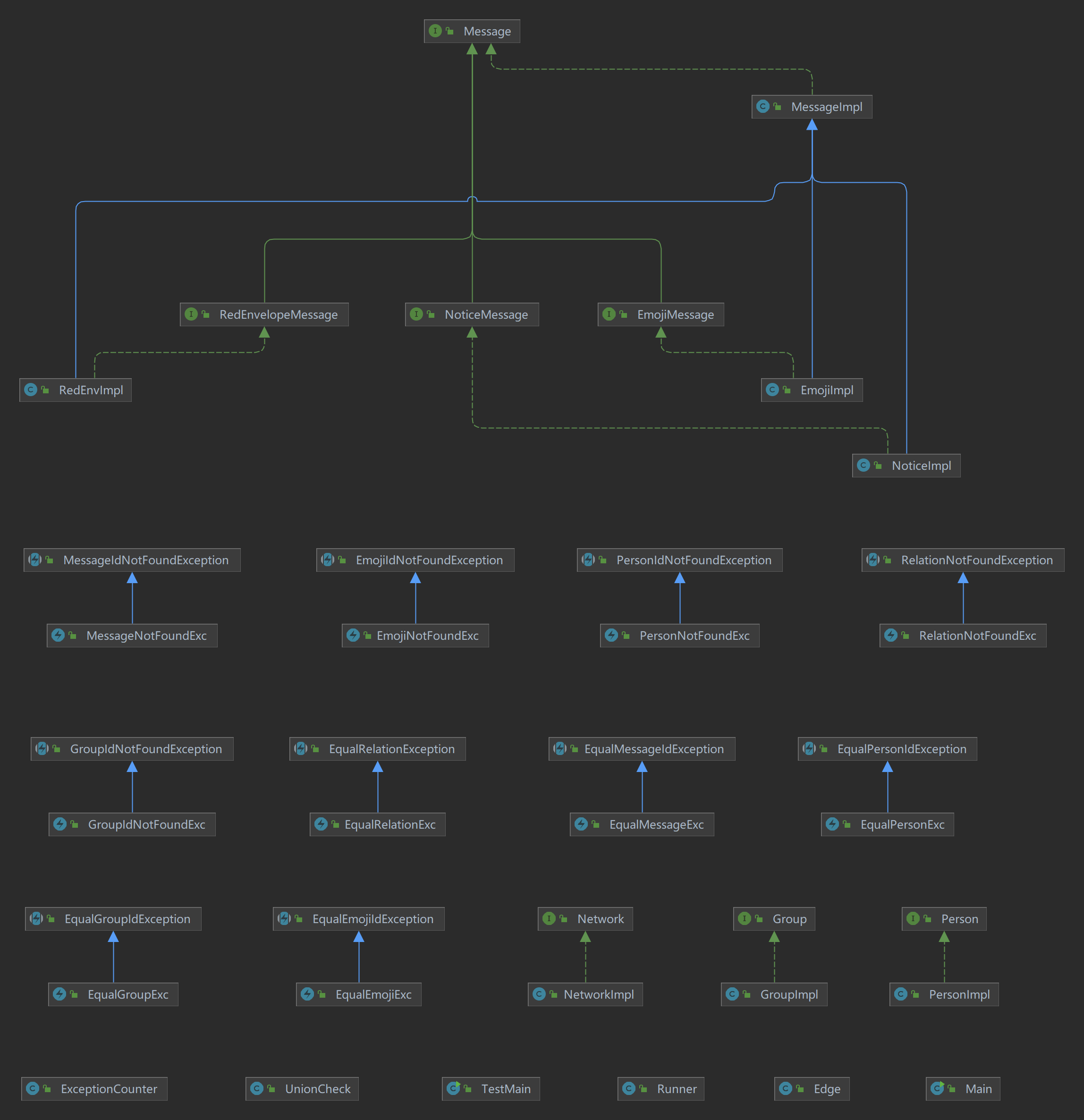
（版面所限，只展示最终的类图部分内容）

除了题目中必须实现的接口和继承的异常类，我只添加了三个主要的类，分别是：异常计数器ExceptionCounter、并查集UnionCheck和边Edge。其中异常计数器和并查集都使用了单例模式方便访问并保证了数据的一致性。

对于Edge，只是简单存储了关系的两个端点和社交值。大致的属性和方法如下：

public class Edge {

    private final int id1;
    private final int id2;
    private final int value;

    public Edge(int id1, int id2, int value) {
        this.id1 = id1;
        this.id2 = id2;
        this.value = value;
    }

    public int getId1() {
        return id1;
    }

    public int getId2() {
        return id2;
    }
    
    public int getValue() {
        return value;
    }
}

✔算法设计

本文不会详细介绍各个算法的具体原理，仅讨论应用方面的内容。

📱并查集

qci指令要求查询两个人之间的连通性，即无向图中两点的连通性，考虑用路径压缩的并查集实现（不用路径压缩也可以）。

UnionCheck类就是单例模式的全局并查集实现类，具体代码如下：

public class UnionCheck {

    private static final UnionCheck UNION = new UnionCheck();
    private static final HashMap<Integer, Integer> DATA = new HashMap<>();

    public static UnionCheck fetch() {
        return UNION;
    }

    public static final ArrayList<Edge> EDGES = new ArrayList<>();

    public void addPerson(int id) {
        DATA.put(id, id);
    }

    public void merge(int id1, int id2) {
        DATA.compute(find(id1),(k, v) -> find(id2));
    }

    public int find(int i) {
        if (DATA.get(i) == i) {
            return i;
        } else {
            // simplify
            DATA.put(i, find(DATA.get(i)));
            return DATA.get(i);
        }
    }

    public void addEdge(Edge edge) {
        EDGES.add(edge);
    }

    public ArrayList<Edge> getSortedEdges() {
        EDGES.sort(Comparator.comparingInt(Edge::getValue));
        return EDGES;
    }

}

其中最后一个方法getSortedEdge()是为了实现kruskal算法而使用的，目的是将现存的所有关系（也就是边）按照社交值（也就是边权）从小到大排序并返回。当然也可以用优先队列实现，这样就不用每次调用都排序一次，降低了时间复杂度。

💻Kruskal算法

qlc指令需要我们给出图中包含某个顶点的最小生成树的边权之和。根据本单元作业的数据规模，只需要考虑稀疏图的情况，于是选用复杂度相对较低的Kruskal算法。其中需要重新建立一个顶点所在连通分量的小规模并查集，每添加一条边之前都判断获得的边之间会不会生成环路。具体代码实现如下：

    @Override
    public int queryLeastConnection(int id) throws PersonIdNotFoundException {
        if (!contains(id)) {
            throw new PersonNotFoundExc(id);
        }
        ArrayList<Edge> edges = UnionCheck.fetch().getSortedEdges();
        ArrayList<Edge> originEdges = new ArrayList<>();
        HashMap<Integer, Integer> union = new HashMap<>();
        // initialize union & originEdges
        int i;
        for (i = 0; i < edges.size(); i++) {
            if ((UnionCheck.fetch().find(edges.get(i).getId1()) == UnionCheck.fetch().find(id))) {
                if (!union.containsKey(edges.get(i).getId1())) {
                    union.put(edges.get(i).getId1(), edges.get(i).getId1());
                }
                if (!union.containsKey(edges.get(i).getId2())) {
                    union.put(edges.get(i).getId2(), edges.get(i).getId2());
                }
                originEdges.add(edges.get(i));
            }
        }
        // kruskal
        int ret = 0;
        int size = originEdges.size();
        int cnt = 0;
        for (i = 0; i < size; i++) {
            Edge e = originEdges.get(i);
            int a = e.getId1();
            int b = e.getId2();
            int val = e.getValue();
            if (find(a, union) != find(b, union)) {
                merge(a, b, union);
                ret += val;
                cnt++;
            }
            if (cnt >= union.size() - 1) {
                break;
            }
        }
        return ret;
    }

🧵Dijkstra算法

sim指令要求我们给出两个人之间的最短路径，考虑使用复杂度较低且易于实现的Dijkstra算法。在维护排序的路径方面我使用了优先队列的方式以获得较好的性能。具体代码实现如下：

    @Override
    public int sendIndirectMessage(int id) throws MessageIdNotFoundException {
        if (!containsMessage(id) || containsMessage(id) && getMessage(id).getType() == 1) {
            throw new MessageNotFoundExc(id);
        }
        int id1 = getMessage(id).getPerson1().getId();
        int id2 = getMessage(id).getPerson2().getId();
        try {
            if (!isCircle(id1, id2)) {
                return -1;
            }
        } catch (PersonIdNotFoundException ignored) {
        }
        Person p1 = getPerson(id1);
        Person p2 = getPerson(id2);
        p1.addSocialValue(getMessage(id).getSocialValue());
        p2.addSocialValue(getMessage(id).getSocialValue());
        Message m = getMessage(id);
        if (m instanceof RedEnvelopeMessage) {
            p1.addMoney(-((RedEnvImpl) m).getMoney());
            p2.addMoney(((RedEnvImpl) m).getMoney());
        } else if (m instanceof EmojiMessage) {
            emojiHeatList.computeIfPresent(((EmojiMessage) m).getEmojiId(), (k, v) -> v + 1);
        }
        ((LinkedList<Message>) p2.getMessages()).addFirst(m);
        messages.remove(m.getId());
        HashMap<Integer, Integer> distance = new HashMap<>();
        HashSet<Person> solved = new HashSet<>();
        PriorityQueue<Person> unsolved =
                new PriorityQueue<>(Comparator.comparingInt(o -> distance.get(o.getId())));
        for (Person p : people.values()) {
            if (p.equals(p1)) {
                distance.put(p.getId(), p.queryValue(p1));
                solved.add(p);
            } else {
                distance.put(p.getId(), p.isLinked(p1) ? p.queryValue(p1) : Integer.MAX_VALUE);
                unsolved.add(p);
            }
        }
        while (!unsolved.isEmpty()) {
            // find the closest vertex around S in (V - S)
            Person closestPerson = unsolved.poll();
            solved.add(closestPerson);
            // refresh the vertices around closestPerson in (V - S)
            for (Person pp : ((PersonImpl) closestPerson).getAcquaintance().values()) {
                if (distance.get(pp.getId()) >
                        distance.get(closestPerson.getId()) + closestPerson.queryValue(pp) &&
                        unsolved.contains(pp) && !solved.contains(pp)) {
                    unsolved.remove(pp);
                    distance.put(pp.getId(),
                            distance.get(closestPerson.getId()) + closestPerson.queryValue(pp));
                    unsolved.add(pp);
                }
            }
        }
        return distance.get(id2);
    }

初始状态为：V = {StartPoint}, S = VertexSet - {StartPoint}，然后不断在S中寻找距离点集V最近的点P，将其从V中去掉并加入S，更新所有S中点的距离后进入下一个循环直到S = {}。这里有一个可以优化性能的点，那就是在更新S中其他点的距离时不需要便利所有点，只需要在P的邻居之间寻找即可，而在本次作业中每个人都记录了自己认识的人的集合，所以直接遍历这个集合并更新距离即可。最后的实验也证明了这样的效率是很高的。

🎈本地测试数据

在自己的本地测试中主要是随机生成的数据点，因为程序预先设计了许多异常，并有异常对应的特殊输出，所以数据点可以随机进行生成。主要是根据Random rand; int p = rand.nextInt();给出的p值设置一些区间来生成数据。当然根据一些特定指令可以手写一些小规模的针对性测试点。

在测试过程中我借用了室友的评测机进行对拍。据我所知，该评测机可以生成随机测试点和针对性测试点。针对性测试点主要是测试需要用到图论算法的指令（比如qgvs和sim等），生成一些极端的数据看是否会超时。

🛰性能问题和修复情况

1️⃣并查集出现StackOverFlow

第一次作业并查集类中的find()函数使用了路径压缩的方法，把每个被查询的点直接连接到其祖先。由于当时不清楚HashMap中的put()方法遇到重复的键会直接改写，我使用了computeIfPresent()方法来改写。这种处理方法会在函数迭代次数过多的情况下导致栈溢出的异常。

2️⃣`qgvs`指令超时

qgvs指令需要计算一个组当中每个人对其他人的社交值的和，计算一次的时间复杂度是\(O(n^2)\)，因此互测中可能会有人大量调用该指令来hack。我首先想到的解决办法是在第一次调用qgvs k的时候将k组的对应值算出来并储存，然后之后每次调用的时候只需读取储存的值即可。当然在atg/dfg之后需要修改储存的值，需要将之前储存的值\(val\)加上或减去\(2\sum_{p \in P's\ acquaintance}SV_p\)。但是在实现之后总是有bug并且我一直没有发现问题出在哪里，于是采用了一个拙劣的方法：维护一个private boolean modified来记录“在上次qgvs并存储之后这个组的成员有没有被修改”（初始值为true），这样如果连续qgvs轰炸就不用重新计算。当然如果边修改组内成员边qgvs则还是有超时的可能，这也是迫不得已的方法。

🚀`Network`拓展JML

  /*@ public normal_behavior
	@ ensure
	@ (\exist i; 0 <= i && i < advertisers.length;advertisers[i].isLinked(getMessage(id).getPerson2())) && advertisers[i].isLinked(getMessage(id).getPerson1()))
	@ assignable getMessage(id).getPerson2().messages
	@ ensures getMessage(id).getPerson2().messages.length = (getMessage(id).getPerson2().messages.length) + 1 
	@ ensures (\forall int i; 0 <= i && i < \old(getMessage(id).getPerson2().getMessages().size());
	@          \old(getMessage(id)).getPerson2().getMessages().get(i+1) == \old(getMessage(id).getPerson2().getMessages().get(i)));
	@ ensures \old(getMessage(id)).getPerson2().getMessages().get(0).equals(\old(getMessage(id)));
	@ assignable getMessage(id).getPerson2().money
	@ getMessage(id).getPerson2().money = \old(getMessage(id).getPerson2().money) + getMessage(id).getsocialValue()
	@ ensures &!containsMessage(id) && messages.length == \old(messages.length) - 1 &
	@         (\forall int i; 0 <= i && i < \old(messages.length) && \old(messages[i].getId()) != id;
	@         (\exists int j; 0 <= j && j < messages.length; messages[j].equals(\old(messages[i]))));
	@ also
	@ public exceptional_behavior
	@ signals (PersonIdNotFoundException e) 
	@ (\forall i; 0 <= i && i < customers.length;!customers[i].equals(getMessage(id).getPerson1())) ||
	@ (\forall i; 0 <= i && i < producers.length;!producers[i].equals(getMessage(id).getPerson2()))
	@ signals (RelationNotFoundException e) 
	@ (\forall i; 0 <= i && i < advertisers.length;!advertisers[i].isLinked(getMessage(id).getPerson2())) || !advertisers[i].isLinked(getMessage(id).getPerson1()))
	@*/
public void purchase(int personID) throws PersonIdMotFoundException, RelationNotFoundException;

/*@ public normal_behavior
  @ requires contains(ads.getProducer()) && contains(ads.getAdvertiser());
  @ assignable people[*].money, ((Producer) people[*]).sales;
  @ ensures (\forall int i;0 <= i && i < people.length;
  @          (people[i] instanceof Producer && ads.getProducer().getId == people[i].getId()) ==>
  @           people[i].money = \old(people[i].getMoney()) - (ads.getCost()) +
  @           (\sum int j;0 <= j && j < people.length && people[j] instanceof Consumer && ((Consumer) people[j]).wantsToBuy(ads.getProduct());
  @            ads.getPrice())));
  @ ensures (\forall int i;0 <= i && i < people.length;
  @          (people[i] instanceof Producer && ads.getProducer().getId == people[i].getId()) ==>
  @           ((Producer) people[i]).sales = \old(((Producer) people[i]).getSales()) + 
  @           (\sum int j;0 <= j && j < people.length && people[j] instanceof Consumer && ((Consumer) people[j]).wantsToBuy(ads.getProduct());
  @            1)));
  @ ensures (\forall int i;0 <= i && i < people.length;
  @          (people[i] instanceof Advertiser && ads.getAdvertiser().getId() == people[i].getId()) ==>
  @           people[i].money = \old(people[i].getMoney()) + ads.getCost());
  @ ensures (\forall int i;0 <= i && i < people.length;
  @          (people[i] instanceof Consumer && people[i].wantsToBuy(ads.getProduct())) ==>
  @           people[i].money = \old(people[i].getMoney()) - ads.getPrice());
  @ ensures (\forall int i;0 <= i && i < people.lenght;
  @          !(people[i] instanceof Producer || people[i] instanceof Consumer || people[i] instanceof Advertiser) ==>
  @           \not_assigned(people[i].money));
  @ also
  @ public exceptional_behavior
  @ signals (ProducerNotFoundException e) !contains(ads.getProducer()) ||
  @                                       (contains(ads.getProducer()) && !(getPerson(ads.getProducer()) instacnceof Producer));
  @ also
  @ public exceptional_behavior
  @ signals (AdvertiserNotFoundException e) contains(ads.getProducer()) && getPerson(ads.getProducer() instacnceof Producer)) &&
  @                                         (!contains(ads.getProducer()) ||
  @                                          (contains(ads.getProducer()) && !(getPerson(ads.getProducer()) instacnceof Producer)));
  @*/
public void publishAdvertisement(Advertisement advertisement) throws
    ProducerNotFoundException, AdvertiserNotFoundException;

  /*@ public normal_behavior
	@ requires containsProductId(productId);
	@ ensures \result == productList(id).getSalesAmount();
	@ also
	@ public exceptional_behavior
	@ signals (ProductNotFoundException e) !containsProduct(productId);
	@*/
public int querySaleAmount(int productId) throws ProductNotFoundException；

🤔心得与体会

第三单元是互测的最后一个单元，本学期的圣杯战争终于告一段落。~~（悲）~~

本单元作业相比前两个单元确实要简单一些，如果不写评测机和测试点生成程序的话基本上没有什么压力。对于大部分函数来说只要跟着JML写就可以（大概）保证正确性，一些需要考虑图论算法和JML很长的函数也不会带来很大负担。不过由于JML的复杂性，有一些细节很容易被遗漏，所以这个单元比前两个单元更容易出bug。好在课程组好心没有在强测中出极端数据，这样我的两个bug没有影响到强测😀。

助教说这单元的重点是阅读JML并给出能保证正确性的代码实现，而不是算法。个人感觉也是如此，算法超时造成的损失一定比遗漏某些细节造成的损失大，但是实现算法的过程比阅读JML要有趣很多（划）。说到底也是个tradeoff吧，契约式编程能够保证程序实现的正确性，不存在自然语言的多义性，但是读懂并理解JML的含义并不是轻松的工作，比如求最小生成树函数的JML就非常长，而且JML所表述的内容很抽象，完全理解需要来来回回读好几遍。个人感觉JML在一些情况下可能会浪费时间：还是上面的例子，需求者可以直接传达“求组内包含某个点的最小生成树”的信息，这样比JML要便捷许多，也不用花费心思用数组来抽象树的结构，在编写和理解两端都要耗费不少精力。当然在大多数环境下为了保证代码严格的正确性，以及完整严谨地传达用户的请求（据荣文戈老师所言，用户是很可怕的😱），还是有必要进行契约式编程的。

posted @ 2022-06-01 22:50 alxzzz 阅读(43) 评论(1) 收藏举报

刷新页面返回顶部

alxzzz

BUAA OO 第三单元总结

BUAA OO 第三单元总结

🖊概述

🗺架构设计

✔算法设计

📱并查集

💻Kruskal算法

🧵Dijkstra算法

🎈本地测试数据

🛰性能问题和修复情况

1️⃣并查集出现StackOverFlow

2️⃣qgvs指令超时

🚀Network拓展JML

🤔心得与体会

公告

2️⃣`qgvs`指令超时

🚀`Network`拓展JML