30-奇异值分解
一、背景介绍
奇异值分解（Singular value decomposition）简称SVD，是将矩阵分解为特征值和特征向量的另一种方法。
奇异值分解可以将一个比较复杂的矩阵用更小更简单的几个子矩阵相乘来表示，这些小矩阵描述的都是矩阵的重要的特性。
奇异值分解在图形降噪、推荐系统中都有很重要的应用。
对于任意矩阵$A$，都可以奇异值分解成下面的形式：
$A = U\sum V^T$，其中$U,V$是正交矩阵，$\sum$是对角矩阵
如果$A$是正定矩阵（肯定对称：对称矩阵）的话：
$A = Q\sum Q^T$
即用一个正交矩阵$Q$就可以使$A$进行奇异值分解，不需要两个
对于一个普通的可对角化的矩阵$A$来说：
$A = S\Lambda S^{-1}$
但这种形式下的特征向量矩阵$S$并不是正交矩阵，而SVD要求$U$和$V$都是正交矩阵
二、奇异值分解的目标
$A$是$m* n$的矩阵，四个基本子空间的正交性可以用下图表示，其中$r$是矩阵的秩
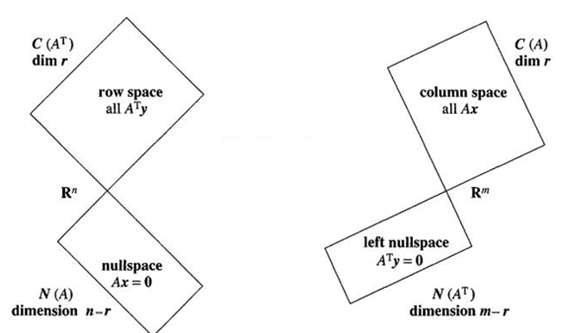
可以把矩阵$A$看作一种线性变换操作，将其行空间中的每一个向量$v$，变换为列空间的向量$u$，即$u=Av$。
类似地，我们也可以在行空间中找到一组正交基，通过矩阵$A$线性变换成列空间中的另一组正交基：
行空间中的一组正交基可以通过格拉姆-施密特正交化得到——任意一组基都可以通过格拉姆-施密特正交化变成一组正交基
但是随便一组正交基（正交基有很多组，如二维中$x,y$轴是一组，$x,y$轴顺时针旋转45度又是一组正交基）经过矩阵$A$的线性变换后的向量却未必正交，因此这组满足要求的正交基非常特殊，它们需要满足：
更进一步，在$V$中寻找标准正交向量，经过$A$的线性变换后使$U$中的向量标准化，从而使$U$和$V$标准正交
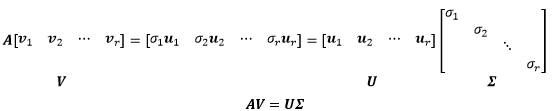
其中$v_i, u_i$都是单位向量，$\sigma_i$是$u_i$的倍数，称为奇异值
上式就是奇异值分解的目标：寻找行空间的一组标准正交基，通过$A$变成列空间的一组标准正交基
由于$V$中的向量的都是正交向量，因此$VV^T=I$：
$AV=U\sum$
$AVV^T=U\sum V^T$
$A=U\sum V^T$
这正是奇异值分解的形式
三、如何分解
我们已经知道奇异值分解的目标是$A=U\sum V^T$，现在的问题是怎样找到合适的正交矩阵$U$和$V$？
一下子两个未知数，不好解决，考虑首先解决$U$和$V$中的一个，先将$U$消去：
注意到：$A^TA$一个对称方阵，并且符合正定矩阵正交分解的形式
$V$就是$A^TA$的特征向量，$\sigma_i^2$就是$A^TA$的特征值，$\sigma_i$取特征值的正平方根
四、正交向量的方向问题
$A = \left[\begin{array}{ll}{4} & {4} \\ {-3} & {3}\end{array}\right]$，求$A$的奇异值分解
目标：$A = U\sum V^T$，先求解$V$：
$A^TA = \left[\begin{array}{ll}{4} & {-3} \\ {4} & {3}\end{array}\right]\left[\begin{array}{ll}{4} & {4} \\ {-3} & {3}\end{array}\right]=\left[\begin{array}{ll}{25} & {7} \\ {7} & {25}\end{array}\right]$
计算特征值和特征向量：
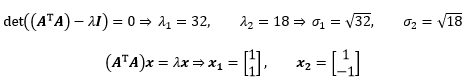
将特征向量标准化：
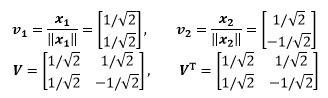
现在我们有了下面的式子：
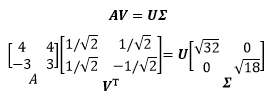
通过上式可以进一步求得$U$，但是我们打算用和求$V$同样的方式求得$U$：
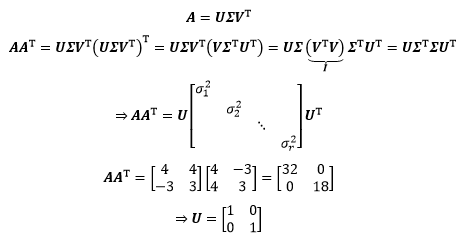
好了，现在验证一下奇异值分解的结果：
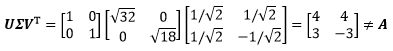
这个结果并不等于$A$，问题出在哪呢？
我们注意到，如果$U$的一个向量反向，$U$中的两个向量仍然是正交向量，且此时可以完成奇异值分解：
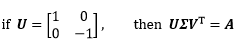
这是因为在奇异值分解的过程中，一旦确认了$V$中向量的方向之后，$U$中向量的方向也一起被限定了
而在本例中，我们用一种和$V$无关的方式求得了$U$，而这种方法并不一定总是有效，需要尝试改变向量的方向
五、奇异矩阵的奇异值分解
奇异矩阵$A$也可以进行奇异值分解，求矩阵$A = \left[\begin{array}{ll}{4} & {3} \\ {8} & {6}\end{array}\right]$的奇异值分解
$A$是秩$1$矩阵。容易看出$A$的行空间的基是$v_1 = [4, 3]$，行空间是一维的，与之垂直的向量在零空间上$v_2 = [3, -4]$
$A$的列空间也是一维的，$u_1 = [1, 2]$，与之垂直的向量在左零空间上，$u_2 = [2, -1]$，将上面的4个向量标准化，得到4个新的向量：
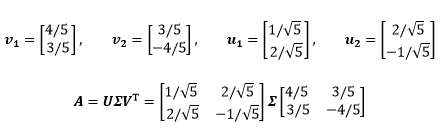
接下来通过$A^TA$的特征向量求得$\sum$
$A^TA = \left[\begin{array}{ll}{4} & {8} \\ {3} & {6}\end{array}\right]\left[\begin{array}{ll}{4} & {3} \\ {8} & {6}\end{array}\right]=\left[\begin{array}{ll}{80} & {60} \\ {60} & {45}\end{array}\right]$
$A^TA$也是一个秩1矩阵，因此可确定一个特征值是0，通过矩阵的迹可确定另一个特征值是125，由此得到了$\sum$：
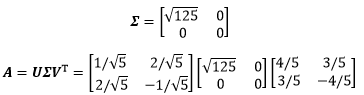
六、致谢
本文参考，感谢作者分享，知识共享，改变世界！
