斐波那契查找不再迷惑
裴波那契查找的来源
裴波那契数列是一串按照F(0)=1,F(1)=1, F(n)=F(n-1)+F(n-2)(n>=2,n∈N*)这一条件递增的一串数字:
1、1、2、3、5、8、13、21 ... ...两个相邻项的比值会逐渐逼近0.618 —— 黄金分割比值。这个非常神奇的数列在物理,化学等各大领域上有相当的作用, 于是大家想: 能不能把它用在查找算法上嘞??
于是就有了裴波那契查找算法,
裴波那契数列最重要的一个性质是每个数都等于前两个数之和(从第三个数字开始)。
也就是一个长度为f(n)的数组,它能被分成f(n-1)和f(n-2)这两半,
而f(n-1)又能被分为f(n-2)和f(n-3)这两半。。。直到分到1和1为止(f(1)和f(2))。
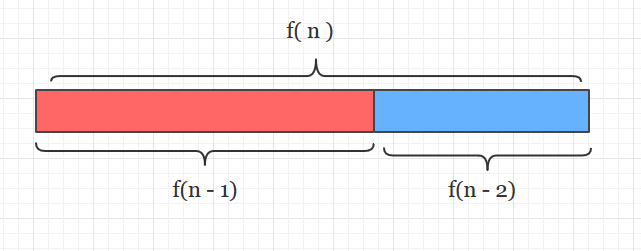
(注意一个细节: 在分割时,可以选择将“大块”的f(n-1)放前面部分,也可以将“小块”的f(n-2)放前面,我下面的分割都是按照“大块”在前进行的)
这里我们发现,二分查找, 插值查找和裴波那契查找的基础其实都是:对数组进行分割, 只是各自的标准不同: 二分是从数组的一半分, 插值是按预测的位置分, 而裴波那契是按它数列的数值分。
三个数组以及它们之间的关系。
了解裴波那契查找的算法实现, 最重要的是理解“三个数组”之间的关系,它们分别是:
- 待查找数组 (a)
- 裴波那契数组(fiboArray)
- 填充后数组(filledArray)
裴波那契数组
要按裴波那契数分割, 我们当然要创建一个容纳有裴波那契数的数组,那么,怎么确定这个数组的长度呢? 或者说, 怎么确定数组里裴波那契数的最大值呢?(最后一个值)
答:只要刚好能满足我们的需要就可以了,裴波那契数组的长度,取的是大于等于待查找数组长度的最小值。原数组长4则取5,长6则取8,长13取13(1、1、2、3、5、8、13、21 )
填充数组
其次我们要考虑的是: 我们的数组长度不可能总是满足裴波那契数的, 例如5、8、13、21等是裴波那契数, 但我们的数组长度可能是6,7,10这些非裴波那契数, 那这时候怎么办呢? 总不能对长度为10的待查找数组按照8和13进行第一次分割吧, 所以我们应该按照上面选定的裴波那契数组的最大值, 创建一个等于该长度的填充数组, 将待查找数组的元素依次拷贝到填充数组中, 剩下的部分用原待查找数组的最大值填满。
我们进行查找操作的并不是原待排序数组, 而是对应的填充数组!
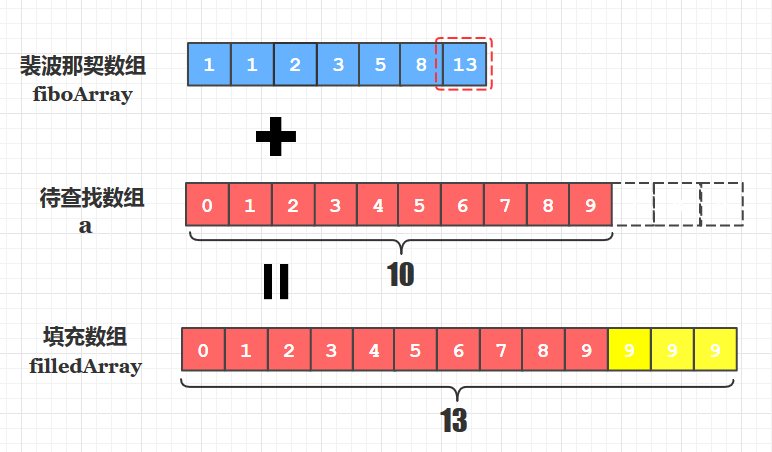
查找到填充的部分元素如何处理?
当我们在填充数组中查找成功后,该元素可能来源于在原数组的基础上填充的部分元素(上图黄色9), 返回的下标(10,11,12)显然是不准确的,而应该返回原数组的最后一个元素的下标(9) 。
所以,解决方法就是: 在填充数组中查找成功后, 判断返回的元素下标和原数组长度的关系,如果:返回下标 > 原数组长度 - 1, 那么改为返回原数组最后一个元素下标就OK了。
查找过程
OK,有了上面的基础我们总结下查找的过程:
- 根据待查找数组长度确定裴波那契数组的长度(或最大元素值)
- 根据1中长度创建该长度的裴波那契数组,再通过F(0)=1,F(1)=1, F(n)=F(n-1)+F(n-2)生成裴波那契数列为数组赋值
- 以2中的裴波那契数组的最大值为长度创建填充数组,将原待排序数组元素拷贝到填充数组中来, 如果有剩余的未赋值元素, 用原待排序数组的最后一个元素值填充
- 针对填充数组进行关键字查找, 查找成功后记得判断该元素是否来源于后来填充的那部分元素
具体代码
package find;
import java.util.Scanner;
public class FibonacciSearch {
public static void main(String[] args) {
int[] a={0,1,2,3,4,5,6,7,8,9};
System.out.println("请输入想要查找的数值:");
Scanner sc=new Scanner(System.in);
int key=sc.nextInt();
int s=search(a,key);
if(s==-1){
System.out.println("没有这个数据");
}else{
System.out.println("查到数据下标为"+s);
System.out.println("查到数据为第"+(s+1)+"个数");
}
}
/**
* @param a: 待查找的数组
* @description: 创建最大值刚好>=待查找数组长度的裴波纳契数组
*/
private static int[] makeFiboArray(int[] a) {
int N = a.length;
int first = 1, sec = 1, third = 2, fbLength = 2;
int higt = a[N - 1];
while (third < N) { // 使得裴波那契数不断递增,直到值刚好大于等于原数组长度为止
third = first + sec; // 根据f(n) = f(n-1)+ f(n-2)计算
first = sec;
sec = third;
fbLength++;// 计算最后得到的裴波那契数组的长度
}
int[] fb = new int[fbLength]; // 根据上面计算的长度创建一个空数组
fb[0] = 1; // 第一和一二个数是迭代计算裴波那契数的基础
fb[1] = 1;
for (int i = 2; i < fbLength; i++) {
fb[i] = fb[i - 1] + fb[i - 2]; // 将计算出的裴波那契数依次放入上面的空数组中
}
return fb;
}
/**
* @description: 裴波那契查找
*/
public static int search(int[] a, int key) {
int low, high;
int lastA;
int[] fiboArray = makeFiboArray(a);//// 创建最大值刚好>=待查找数组长度的裴波纳契数组
int filledLength = fiboArray[fiboArray.length - 1];//创建填充数组长度
int[] filledArray = new int[filledLength];// 创建长度等于裴波那契数组最大值的填充数组
for (int i = 0; i < a.length; i++) {
filledArray[i] = a[i];// 将原待排序数组的元素都放入填充数组中
}
lastA = a[a.length - 1];//// 原待排序数组的最后一个值
for (int i = a.length; i < filledLength; i++) {
filledArray[i] = lastA;//// 如果填充数组还有空的元素,用原数组最后一个元素值填满
}
low = 0;
high = a.length; // 取得原待排序数组的长度 (注意是原数组!)
int mid;
int k = fiboArray.length - 1;
while (low <= high) {
mid = low + fiboArray[k - 1] - 1;
if (key < filledArray[mid]) {
high = mid - 1;//排除右半边的元素
k = k - 1;//f(k-1)是左半边的长度
} else if (key > filledArray[mid]) {
low = mid - 1;//排除左半边的元素
k = k - 2;//f(k-2)是右半边的长度
} else {
if (mid > high) {//说明取得了填充数组末尾的重复元素了
return high;
} else {
return mid;//说明没有取到填充数组末尾的重复元素
}
}
}
return -1;
}
}
斐波那契查找的轨迹

不依赖数组的斐波那契查找
我百度“斐波那契查找”的时候, 一大部分基于数组实现的代码都是创建了一个长度固定为20的斐波那契数组。
而第20个斐波那契数是6765,所以这样的代码只能处理长度小于等于6765的数组。
于是就有了另一种编写斐波那契数组的方法: 不依赖数组的编码方法
请点这里:
说一下这种方法和我上面介绍的方法的不同点
- 我上面介绍的版本: 先把斐波那契数算出来,再全部用数组存起来, 要用的时候直接从数组里拿就可以了
- 这个版本: 不用数组存, 只算出来需要的最大的斐波那契数, 要用的时候“临时”计算就可以了
二分,插值和裴波纳契查找的性能比较
二分查找:
二分查找的轨迹可以用一颗判定树来表示,例如:将下面的[20,30,40,50,80,90,100]表示为一颗判定树, 因为一开始查找的是位于整个数组1/2 位置的元素50, 所以将50置于根元素位置, 接下来查找的是30或90,所以放到50的子节点的位置。
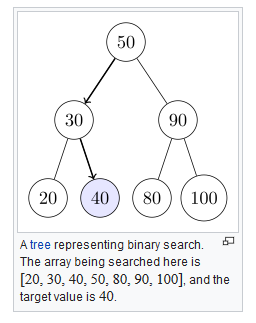
结合一个结论:具有n个节点的判定树的深度为logn2 + 1, 所以二分查找时候比较次数最多为logn2 + 1,
插值查找
上面也说过了,插值查找只适用于关键字均匀分布的表,在这种情况下, 它的平均性能比二分查找好,在关键字不是均匀分布时, 它的性能表现就不足人意了。
斐波那契查找
斐波那契查找的平均性能比二分查找好, 但最坏情况下的性能(虽然仍然是O(logn))却比二分查找差,它还有一个优点就是分割时候只需进行加减运算(二分和插值都有乘/除)






 浙公网安备 33010602011771号
浙公网安备 33010602011771号