【软考】算法

文章目录

• 1* 算法的特点
• 2* 算法类型
• • 2.1 迭代法
  • 2.2 穷举搜索法
  • 2.3 递推法
  • 2.4 递归法
  • 2.5 分治法
  • • 2.5.1 二分法查找
    • 2.5.2 汉诺塔问题
  • 2.6 动态规划法
  • 2.7 回溯法
  • 2.8 贪心法
  • 2.9 分支界限法
  • 2.10 概率算法

1* 算法的特点

a. 有穷性：执行算法的每一步都要在有穷的步骤内完成，每一个步骤都要在有穷的时间内完成；
b. 确定性：每一条指令都有确定的含义；
c. 输入：对于相同的输入，只能产生相同的输出，一个算法具有0…*个输入；
d. 输出：1…*个输出，一个算法没有输出的话，这个算法毫无意义，任何一个算法可以没有输入，但是必须要有输出；
e. 可行性：算法描述的每个操作，都是可以通过已经实现的基本运算的执行来实现的。

2* 算法类型

2.1 迭代法

从某个点出发，通过某种方式求出下一个点，使得其离要求的点（方程的解）更进一步；
当两者之差接近到可接受的精度范围时，就认为找到了问题的解。

2.2 穷举搜索法

一般采用多重循环

例：找出n个自然数（1,2，3，…，n）中r个数的组合，这里假设r=3。

void main()
{
	int i, j, k, n;
	printf (" please input n: ");
	scanf (" %d ", &n );
	for(i=n; i>=1 ; i--)
		for( j=n; j>=1 ; j--)
			for( k=n; k>=1 ;k--)
	if (( i !=j )&& (i != k)&&(j !=k)&&(i>j)&&(j>k))
		printf ("%3d,%3d,%3d/n",i,j,k);
}		

2.3 递推法

层层递推

例：编写程序，对给定的n(n<= 100),计算并输出k的阶乘 k! (k=1,2,…,n)的全部数字。

void pnext(int a[ ] , int k) 
{
	int *b, m=a[0],i,j,r,carry;
	b=(int *) malloc(sizeof(int)*(m+1));
	for(i=1 ; i<=m ; i++)   b[i]=a[i];
	for(j=1 ; j<=m ; j++) 
	{
		for(carry=0, i=1 ; i<=m ; i++)
		{
			r=(i<=a[0]; a[i]+b[i] ; a[i])+carry;
			a[i]=r%10; 
			carry=r/10;
		}
		if (carry) 	a[++m]=carry;
	}
	free(b) ; a[0]=m;
}	

2.4 递归法

递推：从复杂到简单；
回归：从简单回归到复杂

例：编写计算斐波那契数列，数列大小为n。

int F(int n)
{
	if(n==0) return 1;
	if(n==1) return1;
	if(n>1) return F(n-1)+F(n-2);
} 

2.5 分治法

分而治之
分解——解决——合并

该问题的规模缩小到一定程度就可以容易解决
该问题可以分解为若干个规模较小的相同问题
利用该问题分解出的子问题的解可以合并为该问题的解
该问题所分解出的各子问题是相互独立的

2.5.1 二分法查找

function Binary_Search(L,a,b,x)
{
	if (a>b)
		return(-1);
	else
	{
		m=(a+b)/2;
		if(x==L[m])	return(m);
		else if(x>L[m])
			return(Binary_Search(L, m+1,b,x));
		else
			return(Binary_Search(L,a,m-1,x));
	}
}

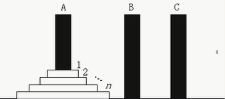
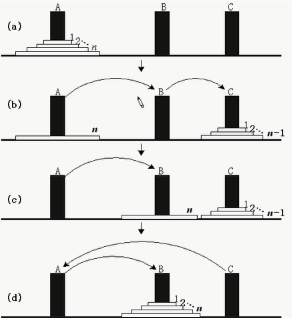
2.5.2 汉诺塔问题

将圆盘从A移动到B，每次只能移动一个，但是必须小的在大的上面

void Hanoi(int n, char A, char B， char C)
{
	if(n>0)
	{
		Hanoi(n-1,A,C,B);
		Move(n,A,B);
		Hanoi(n-1,C,B,A);
	}
}

过程分析：1->B; 2->C; 1->C

2.6 动态规划法

找出最优解的性质，并刻画其结构特征
递归地定义最优值
以自底向上的方式计算出最优值
根据计算最有知识得到的信息，构造最优解

例：最大子段问题

int maxsum(int n, int a)
{
	int sum=0,b=0;
	for(int i=1; i <=n ; i++)
	{
		if(b>0) 	b+=a[i];
		else		b+=a[i];
		if(b>sum)	sum=b;
	}
	return sum;
}

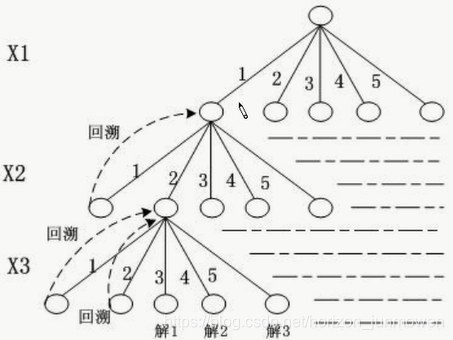
2.7 回溯法

可以系统的搜索问题的所有解
深度优先策略进行搜索
求解组合数较大的问题

int a[MAXN];
void comb(int m, int r)
{
	int i,j,i=0;a[i]=1;
	do
	{
		if(a[i]-i<=m-r+1)
		{
			if(i==r-1)
			{
				for (j=0;j<r;j++)
					printf("%4d",a[j]);
					printf("\n");
				}
			a[i]++;
			continue;
			}
		i++;
		a[i]=a[i-1]+1;
		}
		else
		{
			if(i==0) 	return;
			a[--i]++;
		}
	}
while(1);
}				

2.8 贪心法

在贪心法中采用逐步构造最优解的方法
在每个阶段，都做出一个看上去最优的策略
决策一旦做出，就不可在更改

每一步找到的最优解，组成的整体不一定是最优解

例：哈夫曼编码，找钱（先从面值最大的开始）

2.9 分支界限法

广度优先
最小最大消耗搜索问题解

例：单源最短路径问题

Dijkstra(G,D,s)
{
	S={s}; D[s]=0;
	for(all  i∈V-S)
		D[i]=G[s][i];
	for(i=0;i<n-1;i++)
	{
		D[k]=min[D[i]:	all	 i 	V-S];
		if(D[k]=∞)	return;
		S=S∪{k};
		for(all	j∈V-S)
			if(D[j]>D[k]+G[k][j])	D[j]=D[k]+G[k][j];
	}
}

2.10 概率算法

数值概率算法——近似解，精度随时间增加而增大
Sherwood算法——总能求得解，且正确。减少差别
Las Vegas算法——正确解（要么找不到解，找到的解一定是正确解），改进算法有效性
Monte Carlo算法——求问题准确的解，但解未必是正确的

以上代码仅做参考！