优化建图（线段树、根号）（还在修）

P6348 [PA 2011] Journeys（线段树优化建图模板）

线段树优化建图可以通过线段树来表示点与区间、区间与区间间连边。

区间与区间间连边。所以点与区间间连边被包含在这个问题内。这个可以说是线段树优化建图的模板了。

先搬图。@cymrain07

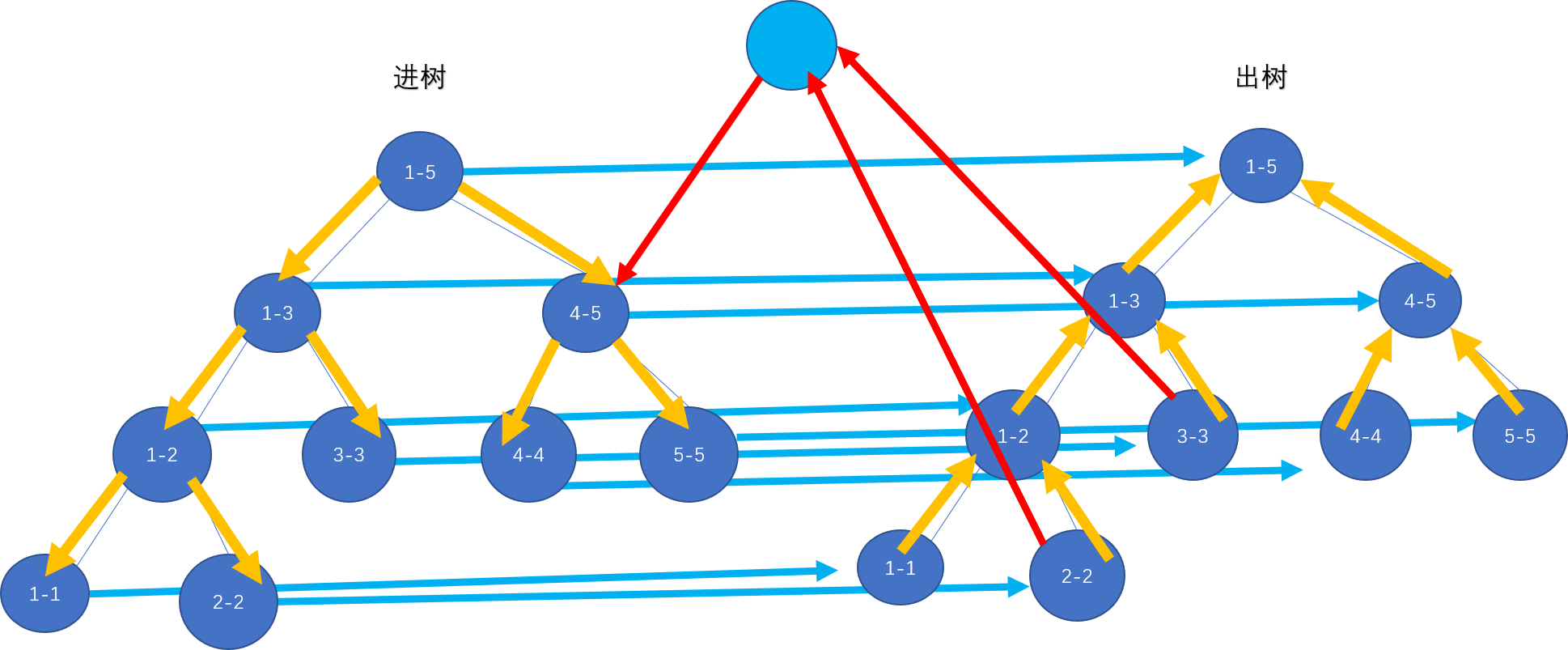
先描述一下如何建树：
将图分为进树和出树，分别是外向树和内向树。然后进树分别向出树的对应节点连边。
如果要区间连边，就分别正常将两个区间拆成 \(\log\) 个点，然后建一个虚拟节点如图对应连边即可。
然后两点间最短路就是正常的最短路。可以发现进树的叶子和出树的叶子间的最短路没有本质差别。

考虑这样为什么是对的。发现线段树的正确性是显然的。如果一个点连向进树上的某一个点就是连向了其下方的所有点。被出树的点连向就是被其下方所有点连向。
然后进树与出树节点的对应连边是因为两棵树的节点在原图的意义上没有本质差别。这样可以保证点走完一条边后可以继续回到出树走。
然后就是对的。

code

但是写了很久。包括但不限于搞错变量名，最短路的起点弄错，连成了单向边，叶子节点提前 return 了导致进树与出树的叶子间没有对应连边。
太菜了。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define pii pair <int,int>
#define mp make_pair
const int N=5e6+7,inf=1e9+7;
vector <pii> q[N];
int n,id[N][2],m,p,dis[N],loc[N];
void add(int u,int v,int w){q[u].push_back(mp(v,w));}
namespace sgt{
    #define ls (u<<1)
    #define rs (u<<1|1)
    #define mid ((l+r)>>1)
    #define idu (id[u][s])
    #define idls (id[ls][s])
    #define idrs (id[rs][s])
    int tot=0;
    void build(int u,int l,int r,int s){
        idu=++tot;
        if(l==r){if(!s)loc[l]=tot,add(idu,id[u][1],0);return;}
        build(ls,l,mid,s),build(rs,mid+1,r,s);
        if(s)add(idls,idu,0),add(idrs,idu,0);
        else add(idu,idls,0),add(idu,idrs,0),add(idu,id[u][1],0);
    }
    void lnk(int u,int l,int r,int ql,int qr,int v,int s){
        if(ql<=l&&r<=qr){
            if(!s)add(v,idu,0);else add(idu,v,1);
            return;
        }
        if(ql<=mid)lnk(ls,l,mid,ql,qr,v,s);
        if(qr>mid)lnk(rs,mid+1,r,ql,qr,v,s);
    }
}
using namespace sgt;
void bfs(){
    for(int i=1;i<=tot;i++)dis[i]=inf;
    deque <int> t;dis[loc[p]]=0;t.push_front(loc[p]);
    while(!t.empty()){
        int u=t.front();t.pop_front();
        for(pii tmp:q[u]){
            int v=tmp.first,w=tmp.second;
            if(dis[v]>dis[u]+w){
                dis[v]=dis[u]+w;
                if(w)t.push_back(v);
                else t.push_front(v);
            }
        }
    }
}
signed main(){
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin>>n>>m>>p;build(1,1,n,1);build(1,1,n,0);
    for(int i=1,a,b,c,d;i<=m;i++){
        int v=++tot;cin>>a>>b>>c>>d;
        lnk(1,1,n,a,b,v,1);lnk(1,1,n,c,d,v,0);
        v=++tot;lnk(1,1,n,c,d,v,1);lnk(1,1,n,a,b,v,0);
    }
    bfs();
    for(int i=1;i<=n;i++)cout<<dis[loc[i]]<<'\n';
    return 0;
}

P5025 [SNOI2017] 炸弹

实际上更是简单题。

考虑这个东西实际上就是点向区间连边。因此只需要进树即可。然后虚拟节点也是不必要的。
然后发现需要缩点。然后就变成了一张 DAG。由于爆炸的炸弹一定是一个连续的区间，因此我们可以对于每一个缩出来的点求其爆炸可以波及的左右端点然后在 DAG 上做类似于 DP 的操作即可。

code

然后因为在 DAG 上 DP 写错了调了一个小时。爆了。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int p=1e9+7,N=2e6+7;
#define pii pair <int,int>
#define mp make_pair
int n,sign[N],mx,du[N],ml[N],mr[N];
vector <pii> q[N];vector <int>fan[N];
void add(int u,int v,int w){q[u].push_back(mp(v,w));}
namespace sgt{
    int id[N],dis[N],loc[N];
    #define ls (u<<1)
    #define rs (u<<1|1)
    #define mid ((l+r)>>1)
    #define idu (id[u])
    #define idls (id[ls])
    #define idrs (id[rs])
    int tot=0;
    void build(int u,int l,int r){
        idu=++tot;
        if(l==r){sign[tot]=l;loc[l]=tot;return;}
        build(ls,l,mid),build(rs,mid+1,r);
        add(idu,idls,0),add(idu,idrs,0);
    }
    void lnk(int u,int l,int r,int ql,int qr,int v){
        if(ql<=l&&r<=qr){add(v,idu,0);return;}
        if(ql<=mid)lnk(ls,l,mid,ql,qr,v);
        if(qr>mid)lnk(rs,mid+1,r,ql,qr,v);
    }
}
using namespace sgt;
int low[N],dfn[N],dfncnt=0,blockcnt,vis[N],stk[N],top,bel[N];
const int M=5e5+7;
int x[M],r[M],a[M],b[M],len,ll[M],rr[M];
vector <int> scc[N];
void tar(int u){
	low[u]=dfn[u]=++dfncnt;vis[u]=1,stk[++top]=u;
	for(pii tmp:q[u]){
		int v=tmp.first;
		if(!dfn[v]){
			tar(v);low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(dfn[v],low[u]);
	}
	if(dfn[u]==low[u]){
		++blockcnt;ml[blockcnt]=p;mr[blockcnt]=-p;
		do{vis[stk[top]]=0;bel[stk[top]]=blockcnt;if(sign[stk[top]])ml[blockcnt]=min(ll[sign[stk[top]]],ml[blockcnt]),mr[blockcnt]=max(rr[sign[stk[top]]],mr[blockcnt]);scc[blockcnt].push_back(stk[top]);}while(stk[top--]!=u);
	}
}
void dfs(int u){
    if(vis[u])return;
    vis[u]=1;
    for(int v:fan[u]){
    	dfs(v);ml[u]=min(ml[u],ml[v]),mr[u]=max(mr[u],mr[v]);
	}
}
signed main(){
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin>>n;for(int i=1;i<=n;i++)cin>>x[i]>>r[i],a[++len]=x[i],b[i]=i;
	a[len+1]=2*p*p;build(1,1,len);
    for(int i=1;i<=n;i++){ll[i]=lower_bound(a+1,a+len+1,x[i]-r[i])-a,rr[i]=upper_bound(a+1,a+len+1,x[i]+r[i])-a-1;lnk(1,1,len,ll[i],rr[i],loc[b[i]]);}
    for(int i=1;i<=tot;i++)if(!dfn[i])tar(i);
    for(int u=1;u<=tot;u++){
        for(pii tmp:q[u]){
            int v=tmp.first;if(bel[u]!=bel[v])fan[bel[u]].push_back(bel[v]);
        }
        vis[u]=0;
    }
    for(int i=1;i<=blockcnt;i++)dfs(i);
	int ans=0;
    for(int i=1;i<=n;i++)ans=(ans+i*(mr[bel[loc[b[i]]]]-ml[bel[loc[b[i]]]]+1ll)%p)%p;
    cout<<ans;return 0;
}
/*
5
-55 7
4 108
53 12
67 17
95 15
*/