P9150 邮箱题 题解

P9150 邮箱题
这个题卡了我一整个下午。主要是感觉题解都写的比较形式化，不是很直观，对于我这种抽象思维比较差的人来说简直就是天书。（当然是我太菜了）
所以个人花了比较多的图来辅助理解。

思路

初步观察

首先我们观察到钥匙这个性质本身是相对强的。如果我们拿到了某个点的钥匙，其下一步能走的点是确定的。但是这个题烦就烦在除了钥匙的限制以外还有一个原图的限制。
比如下面的情况：（注意这个是原图）

假设每个点 \(u\) 有 \(u+1\) 的钥匙，4 有 1 的钥匙。这个时候从 1 开始走就可以到达所有点。因为我们可以在 3 拿到 4 的钥匙后转一圈再到 4。
因此我们考虑把 \(1,2,3\) 这种可以相互到达的结构称为一个强联通分量。

由于钥匙的限制是一一对应的，因此如果我们从某一个点开始一直令 \(u\gets k_u\)，那么最终一定会回到原来的出发点，也就是 \(k\) 序列将原图划分为了很多个环。我们将这个环断开复制一遍，我们就将这个东西所形成的序列称为 \(stk\)。例如，上图中唯一的一个 \(stk\) 序列为 \(\{1,2,3,4,1,2,3,4 \}\)。注意我们会将环断开复制一次，这个可以算是经典操作。同时，这个 \(stk\) 与原图无关，只是由给定的 \(k\) 数组来划分的。一定要分清楚 \(stk\) 形成的环与原图的差别，否则很容易将自己弄晕。

然后我们考虑在 \(stk\) 序列上进行统计答案。由于我们已经断环为链了，因此这个序列上的某个点只能向右一步一步走。
因此，如果我们已经知道了一串后缀的点最多可以走多少点，那我们在统计前面的点的答案的时候这些后缀的点能走到的最多走多少点一定不会变。因此我们考虑从后向前统计答案。

我们继续延续前面维护强联通分量的思路。可以发现一个强联通分量在 \(stk\) 上一定是连续的。我们同时维护最多可以在 \(stk\) 数组上向右走到哪个点。可以发现这个东西在 \(stk\) 上也是一段连续的区间，同时这个区间里的所有点能够走到的最远的点是相同的。也就是说强联通分量以及最多可以走多远的区间又将 \(stk\) 数组划分开来。例如下面是一个例子。

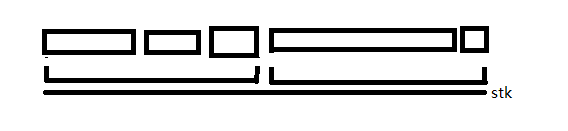
其中方块代表这是一个强联通分量，而区间表示这个区间内的所有点最远都只能到达这个区间的右端点。可以发现一个区间一定完整包含若干个强联通分量。注意，\(stk\) 上一个单独的位置也可以作为一个强联通分量或者一个区间。

同时我们发现，区间右端点与某个点的距离以及这个点所在强联通分量的大小分别就是我们要求的两个问的答案。因此我们去考虑从右往左动态维护区间与强联通分量的信息。

区间合并

我们先考虑插入一个点 \(u\) 后其是否可以合并进与其相邻的区间里。

我们可以发现，\(u\) 作为一个单独的点的时候，能够合并进与其相邻的那个区间（也就是可以走到下一个点）当且仅当 \(u\) 向 \(u\) 在 \(stk\) 上的下一个点有连边才可以。我们设 \(u\) 在 \(stk\) 上的位置为 \(i\)，即 \(stk_{i+1}\) 被 \(stk_i\) 连向。
由于每一个区间在 \(stk\) 上一定是连续的，因此我们对于每一个点都维护一个连向自己的点的位置的最大值，我们设为 \(pre_i\)。这样，如果 \(u\) 是单独一个点，要合并有 \(pre_{i+1}=i\)。

假设 \(u\) 已经合并进了区间里面。现在我们来探究相对长的区间如何合并起来。

（我们先不管强联通分量是如何合并的）
我们假设这个区间的最靠右的点是 \(fa_i\)。当然，这个东西用的并查集快速查找。
那前两个相邻的区间可以合并的充要条件就变成了：$pre_{fa_i+1}\ge i \wedge $ 整个区间都是一个强联通分量。如上图。请注意 \(pre\) 之类的“连边”都是原图上的连边。
这个东西的意思是，只要 \(fa_i+1\) 这个点被 \([i,fa_i]\) 之间的任意一个点连了，那由于强联通分量里面任意的两个点都可以互相到达，所以才可以走完当前区间拿到 \(stk_{fa_i+1}\) 的钥匙之后再走到下一个区间去。注意，\(fa_i\) 本身向 \(fa_i+1\) 就有连边是不可能的，因为如果有边那一开始就会合并进后边的区间。

由于单独一个点本身也算是整个区间都是强联通分量，因此第一个情况可以合并进第二种情况里。

强联通分量合并

现在考虑一个区间内的前两个强联通分量可不可以合并。

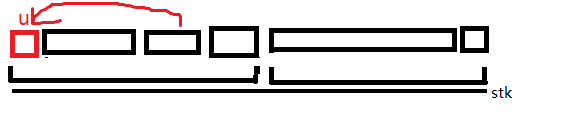
我们维护每一个区间中有类似返祖边的最远的强联通分量，记为 \(loc\)。这个同样可以用并查集将信息挂到区间右端点上。
然后例如上面的图。如果有这样的向前面连的边，那么显然前三个强联通分量都可以合并成一个。当然，注意这个返祖边的标记是一次性的，记得清空。

然后就做完了。

统计答案

最后统计答案的时候就是直接用并查集查找区间和强联通分量的右端点即可。显然当前点是当前所在区间和强联通分量的左端点。

code

细节奇多。注意实现的时候维护区间的并查集和维护强联通分量的并查集要分清楚。
同时，由于 \(k\) 是将原图划分为多个环，因此我们对于每个环都要去处理。
在实现的时候，我们将原图的边通过 vector 挂在了被指向的点上，也就是我们记录的实际上是反边，这个在理解代码时要注意。

#include<bits/stdc++.h>
using namespace std;
const int N=3e6+7;
int n,m,k[N],id[N],vis[N],cnt,stk[N],loc[N],pre[N],ans1[N],ans2[N];//意义基本与题解一样
vector <int> q[N];
struct node{
	int fa[N];
	int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
	void merge(int x,int y){x=find(x),y=find(y);fa[x]=y;}
};node huan;node lian;//huan 和 lian 分别维护强联通分量和区间的右端点

void calc(int beg){
	while(!vis[beg]){stk[++cnt]=beg,id[beg]=cnt,vis[beg]=1;beg=k[beg];}//标记环上的所有点
	for(int i=2*cnt;i>=1;i--){
		int u=stk[(i-1)%cnt+1];huan.fa[i]=lian.fa[i]=i;pre[i]=loc[i]=0;//另类的初始化别忘了
		for(int v:q[u]){
			if(id[v]){
				v=id[v];v=v>i?v-cnt:v;v=v+cnt<i?v+cnt:v;
				pre[i]=max(pre[i],v);v=v<i?v+cnt:v;
				if(v<=cnt*2) loc[lian.find(v)]=max(loc[lian.find(v)],huan.find(v));//找最右端的有返祖边的强联通分量
			}
		}
		while(1){
			while(1){
				int p1=huan.find(i),p2=lian.find(i);
				if(p1<loc[p2])huan.merge(p1,p1+1);else break;  //合并强联通分量
			}
			int p1=huan.find(i),p2=lian.find(i);loc[p2]=0;
			if(p1!=p2||pre[p2+1]<i||p2==2*cnt)break;           //注意这里如果链的右端点已经是区间右端点了也可以跳了
			lian.merge(p2,p2+1);                               //合并区间
		}
		ans1[u]=min(cnt,lian.find(i)-i+1);ans2[u]=min(cnt,huan.find(i)-i+1);//统计答案。由于复制了两次，显然最后一次更新的答案最优（可以统计的区间更长）
	} 
}
void init1(){
	for(int i=1;i<=cnt;i++)id[stk[i]]=0,stk[i]=0;  //注意每次操作后清空序列
	cnt=0;
}
void solve(){
	cin>>n>>m;for(int i=1;i<=n;i++) cin>>k[i];
	for(int i=1,u,v;i<=m;i++) cin>>u>>v,q[v].push_back(u);  //记录的是反边！！！
	for(int i=1;i<=n;i++) if(!vis[i]) calc(i),init1();
	for(int i=1;i<=n;i++) cout<<ans1[i]<<' '<<ans2[i]<<'\n',q[i].clear(),vis[i]=0;//多测不清空，原地见祖宗
}
signed main(){
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	int T;cin>>T;while(T--) solve();
}