KMP

KMP 是线性时间判定模式串 \(s\) 中匹配串 \(t\) 的出现位置的算法。

P3375 【模板】KMP

border

定义串 \(s\) 的 border 是这个串的前缀等于后缀的最长长度。
线性求某个串的 border 是显然的。

我们先要求出 \(t\) 的所有前缀的 border。时间同样要求线性。
假设当前我们当前求到第 \(i\) 位的 border。

假设上一个点的 border 的长度是 \(j\)，那么如果 \(t_{j+1}=t_i\)，那么显然有 \(border_i=j+1\)。
如果不是呢？可以发现如果我们将 \(j\) 一次一次向前移动的话显然会超时。我们考虑利用上我们求出的 border。

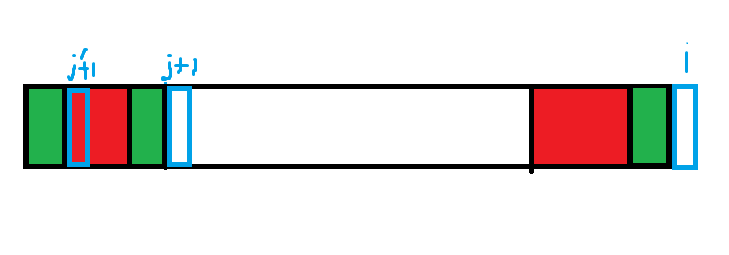
可以发现绿色的三段都是一样的。
发现可能能够继续匹配的最近的点一定是 \(j'=border_j\)。那同样的，如果有 \(t_{j'+1}=t_i\)，那么有 \(border_i=j'+1\)。
如果还不是，就这样一直跳下去即可。如果跳到头了都一直没有那就直接 \(border_i=0\) 即可。

KMP

然后就发现两个子串的匹配与求一个字串的 border 是类似的。
假设 \(s\) 匹配到了第 \(i\) 位，\(t\) 上一次匹配到了第 \(j\) 位。这里的“匹配”是指 \(s\) 的 \([i-j,i-1]\) 位与 \(j\) 的 \([1,j]\) 位全部相同，而现在我们要看第 \(i\) 位是否能够继续匹配上。
如果 \(s_i=t_{j+1}\)，那么显然可以继续匹配，令 \(i\gets i+1,j\gets j+1\) 即可。
如果不是，与刚才类似，\(t\) 最近的能匹配上的可能的位置是 \(border_j\)。画画图就清楚了，从一个串变成两个串而已。
如果 \(j\) 已经与 \(t\) 的长度相等，那直接输出并且准备下一次匹配即可。

code

过于短了。

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+7;
string s1,s2;
int n,m,kmp[N];
signed main(){
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>s1>>s2;n=s1.size(),m=s2.size();s1=' '+s1;s2=' '+s2;
	int j=0;
	for(int i=2;i<=m;i++){
		while(j&&s2[j+1]!=s2[i]) j=kmp[j];
		if(s2[j+1]==s2[i]) j++;
		kmp[i]=j;
	}
	j=0;
	for(int i=1;i<=n;i++){
		while(j&&s2[j+1]!=s1[i]) j=kmp[j];
		if(s2[j+1]==s1[i]) j++;
		if(j==m){cout<<i-m+1<<'\n';j=kmp[j];}
	}
	for(int i=1;i<=m;i++) cout<<kmp[i]<<' ';
	return 0;
}

P4696 [CEOI 2011] Matching

广义 KMP 好题。（？）

实际上，这道题通过类似于 KMP 的原理做了类似于匹配的过程。
我们考虑输入进来的数组与 SA 中的 \(sa\) 数组类似，然后 \(rk\) 数组就是每一个值在位置上的相对大小，于是我们将其映射到 \(rk\) 数组上。

于是我们就要匹配。我们考虑定义所谓“匹配”指 \(h[l,r]\) 与 \(rk[1,r-l+1]\) 两个区间中所有值的相对大小相同。
那么考虑对于 \(h_{r+1}\)，我们怎么判断其是否可以匹配上呢？实际上也就是要满足其与 \(rk_{r-l+2}\) 的相对大小保持不变。
因为我们匹配的一定是 \(rk\) 数组的一个前缀，因此考虑对于 \(rk\) 数组的每一位 \(rk_i\)，求出在前缀 \(rk[1,i-1]\) 中最大的比 \(rk_i\) 小的，最小的比 \(rk_i\) 大的位置。我们称其为 \(L_i,R_i\)。
于是 \(h_{r+1}\) 要满足“匹配”的条件就是

\[h_{r+1}\in (h_{r+1+(L_{r-l+2}-(r-l+2))},h_{r+1+(R_{r-l+2}-(r-l+2))}) \]

看起来不是很好看，我们考虑换一种形式。实际上我们就是要定义“相同”。我们定义在数组 \(s\) 上，\(v\) 与 \(u\) 相同为

\[s_v\in (s_{v+L_u-u},s_{v+R_u-u}) \]

也就是说 \(v\) 要满足 \(u\) 在 \(rk\) 上的相对大小。
然后我们考虑如何求失配指针。由于我们已经定义了“相同”的含义，因此我们发现这个定义在求 border 的时候同样适用。
考虑实际含义就是对于 \(rk\) 的一个前缀，其一段后缀的相对大小与其等长前缀的相对大小相同，例如 \(2,1,3\cdots ,6,4,9\)，那这个序列就有一个长为 3 的 border。
于是我们就形如 KMP 一样去匹配即可。这道题的关键就是定义出所谓“相同”或者说“匹配”的含义。

code

考虑如何预处理前缀的小于的最大和大于的最小。一个简单想法是从头开始扫然后树状数组。一个线性的想法是直接从后往前写一个双向链表直接维护即可。可以用 \(sa\) 数组快速映射到位置。（也算是物尽其用了）

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+7;
int n,m,rk[N],sa[N],h[N],pre[N],nxt[N],L[N],R[N],lnk[N],ans[N],cnt;
void del(int u){nxt[pre[u]]=nxt[u],pre[nxt[u]]=pre[u];}
bool cmp(int *s,int u,int v){if((L[u]&&s[v-u+L[u]]>=s[v])||(R[u]&&s[v-u+R[u]]<=s[v]))return 0;return 1;}
signed main(){
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>n>>m;for(int i=1;i<=n;i++)cin>>sa[i];for(int i=1;i<=n;i++)rk[sa[i]]=i,pre[i]=i-1,nxt[i]=i+1;
	for(int i=n;i>=1;i--){
		int u=rk[i];if(pre[u])L[i]=sa[pre[u]];if(nxt[u]<=n)R[i]=sa[nxt[u]];
		del(u);
	}
	for(int i=2,j=0;i<=n;i++){
		while(j&&!cmp(rk,j+1,i))j=lnk[j];
		if(cmp(rk,j+1,i))j++;lnk[i]=j;
	}
	for(int i=1;i<=m;i++)cin>>h[i];
	for(int i=1,j=0;i<=m;i++){
		while(j&&!cmp(h,j+1,i))j=lnk[j];
		if(cmp(h,j+1,i))j++;if(j==n)ans[++cnt]=i-n+1,j=lnk[j];
	}
	cout<<cnt<<'\n';for(int i=1;i<=cnt;i++)cout<<ans[i]<<' ';return 0;
}