概率DP

概率DP是DP中一个非常重要且较难的DP类型。其题型灵活多变，尤其爱与树形DP结合，同时很可能需要各种数据结构优化。
其主要考点便是DP方程的建立与维护。由于“概率”二字，许多时候分类讨论与小数运算也是不可避免的。
因此，概率DP对选手的逻辑思维与代码能力也有很高的要求，可以说是DP中的集大成者。

P2081 [NOI2012] 迷失游乐园

题意：给定一颗有 \(n\) 个点的树或基环树，每条边有边权 \(w_i\)
求从每个点开始，在树上随机不重地走，最后的期望经过的边权和。
对于每个节点，其下一步走到其任意相邻点的概率是相同的。
数据范围 \(n\le 1e5,w_i \le 100\)

普通树

先考虑在普通的树上怎么做。假设我们先钦定 \(rt\) 为根节点，那么对于每个除根以外的节点，其第一步的走法有两种：

向父亲走
向儿子走
容易发现，如果我们已经求出这个点所有儿子再向下走的概率，那这个点向儿子走的概率转移是朴素的。
设第一步向下走的期望权值为 \(down_u\)，则有

\[{\Large down_u=\frac{\sum_vdown_v+w_{u,v}}{son_u}} \]

其中 \(son_u\) 代表 \(u\) 的儿子个数，\(v\) 代表 \(u\) 的某一个儿子。
而向父亲走的情况稍微复杂了一点。由于这个点走向父亲后还能再向其他儿子走，也可以继续向上，因此情况要考虑完全
设 \(u\) 第一步向上的期望权值为 \(up_u\)，则有

\[{\Large up_u=w_{u,k}+\frac{up_k\cdot fa_k+down_k\cdot son_k-down_u-w_{u,k}}{son_k+fa_k-1}} \]

其中 \(k\) 是 \(u\) 的父亲，\(fa_k\) 是 \(k\) 父亲的数量。这听起来可能有些奇怪，因为普通树中的节点只有一个或没有父亲。
不过在一会要讨论的基环树中，\(fa_u\) 就能体现出作用
\(up_k\cdot fa_k\) 是继续向上走的贡献，\(down_k\cdot son_k\) 是 \(k\) 又向下走的贡献。
但因为不能重复走到 \(u\) 点，因此需要减去贡献。注意上面是总的贡献，因此可以直接减
最后，因为不能走回 \(u\)，因此总共有 \(son_k+fa_k-1\) 种情况。
由于 \(up_u\) 需要由 \(down_u\) 与 \(down_k\) 推出，因此对于普通树，先求 \(down\) 再求 \(up\) 即可。
但需要注意根节点没有父亲，因此处理 \(up\) 时，注意从根节点的所有儿子开始处理。

普通树code

点击查看代码

void make_down(int u,int k)
{
	for(int i=0;i<tot[u];i++)
	{
		int v=q[u][i].v;if(vis[v]||v==k) continue;
		fa[v]=1;make_down(v,u);son[u]++;down[u]+=1.0*(down[v]+q[u][i].w);
	}
	if(son[u]) down[u]=down[u]/son[u];
}
void make_up(int u,int k,ld w)
{
	up[u]=w;
	if(fa[k]+son[k]-1)
	up[u]=up[u]+(up[k]*fa[k]+down[k]*son[k]-down[u]-w)/(son[k]+fa[k]-1);
	for(int i=0;i<tot[u];i++){
		int v=q[u][i].v;if(v==k||vis[v]) continue;
		make_up(v,u,q[u][i].w);
	}
}
void work1()
{
	make_down(1,0);
	for(int i=0;i<tot[1];i++) make_up(q[1][i].v,1,q[1][i].w);
}

基环树

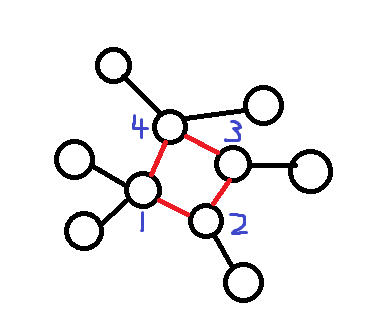
可以先画个图。

非环上节点

红边是环上的边。可以发现，如果我们将红边删掉，就是一片森林，每一个环上的点就是每棵树的根节点
因此对非环点，可以发现其 \(down\) 与 \(up\) 数组的统计是完全一样的。
再多看一眼 \(up\) 的统计。因为对于普通点 \(u\)，其 \(fa_k\) 有可能是2（即 \(u\) 的父亲有可能是环上的点）。
但是事实上这是没有影响的。\(up_k \cdot fa_k\) 统计的仍是继续向上走的总可能权值和，而分母中也正确地考虑了总情况数。
因此，在统计非环上点时，我们仍然可以直接调用上面代码中的 \(madedown\) 与 \(makeup\) 函数

环上节点

对于环上节点，我们仍旧分两种情况。

向其子树走（如果将环上节点视为根）
向其他环上节点走

对于第一种情况，可以发现其实还是与普通树中的情况别无二致。因为 \(down_u\) 数组的维护只与其每个儿子的 \(down\) 值、边权与 \(son\) 有关。
因此还是相同地直接算就行了。
对于第二种情况，我们就将两个联通的环上节点视为相互的父亲，即对于环上节点而言，\(up_u\) 是指走环上的点的期望长度。
发现我们每搜到一个点，其有两种情况：向其子树走，向环上的下一个节点走。向其子树中走的贡献是独立的，加法原理加起来。
向下一个节点走就去下一个节点算。注意由于是等可能的随机游走，因此需要乘上走到这个点的概率。
这么看貌似有些抽象，看个例子：
假设正在统计的 \(u\) 为1号点，先从1号点向2号点这个方向走，那就发现对于2这个节点对1的贡献就是

\[{\Large 走到2的概率\times （\frac{向2的子树走的可能的权值和}{可能的情况数} +2与1间的边权）} \]

由这个特殊的情况拓展一下，考虑一下连续转移的情况

由于游走是等概率的，因此每从一个点 \(u\) 向下一个环上的点统计，走到下一个点的概率就要乘上 \(\frac{1}{son_{u}+1}\)
由于向子树走的数组 \(down\) 已经统计了，因此可能的权值和就是 \(down_u \cdot son_u\)
可能的情况数也就是与当前点相连的边数，但因为不能往回走，因此总情况数为 \(son_u+1\) （那个加一是指向环中下一个点的边）
加上边权的原因是显然的
上述情况中我们都是先假定先向某一个方向走的。实际上向顺、逆时针走的情况是等可能的。最后顺逆时针都跑一遍即可。

综上，我们就大概得出了状态转移方程。对于每个点 \(u\)，其 \(up_u\) 值有

\[{\Large up_u=\sum_{i,v=path_i}{P_{i} \cdot (\frac{down_v \cdot son_v}{son_v+1}+w_{path_{i-1},path_i})}} \]
其中

1.\(path_i\) 为所有环上的点的编号，上面那样的写法是指从 \(u\) 向某一个方向枚举每个环上的节点（也就是说这个方程只包含了一个方向的值）
2. \(w_{path_{i-1},path_i}\) 是指环上相邻两点间的边权
3.\(P_i\) 的值按上文所说，就是走到 \(v\) 这个点的概率。形式化地说，有

\[{\Large P_i=\prod_{j=1}^{i-1}\frac{1}{son_{path_j}}} \]
综上，所有情况的状态与转移都已经清晰。不过记得在处理基环树前先跑两边dfs处理一下环上的信息。
但还是有些实现的小细节：

由于需要跑顺时针逆时针，因此跑之前可以直接将 \(P\) 的初值设为 \(\frac{1}{2}\)
为了 \(O(1)\) 地得到 \(w_{path_{i-1},path_i}\)，可以dfs的时候记录一下环相邻点间的权值
需要先处理 \(down\) 再处理 \(up\)，因为 \(up\) 需要由 \(down\) 转移而来
处理某个点是否为环上的点时需要小心，认真构造

基环树code

点击查看代码

void dfs1(int u,int k)
{
	vis[u]=1;
	for(int i=0;i<tot[u];i++){
		int v=q[u][i].v;if(v==k) continue;
		if(vis[v]) {pos=v;return;}
		dfs1(v,u);
		if(!flag&&pos) {if(pos==u)flag=1;return;}
		if(flag) break;
	}
	vis[u]=0;
}
void dfs2(int u,int k)
{
	dfn[u]=++t;path[t]=u;fa[u]=2;
	for(int i=0;i<tot[u];i++)
	{
		int v=q[u][i].v;if(v==k) continue;
		if(vis[v]) {
			if(!dfn[v]) dfs2(v,u);
			disr[dfn[u]]=disl[dfn[v]]=q[u][i].w;break;
		}
	}
}
#define nxt(x) (x==t?1:x+1)
#define pre(x) (x==1?t:x-1)
void work2()
{
	dfs1(1,0);
	dfs2(pos,0);
	for(int i=1;i<=t;i++) make_down(path[i],0);
	for(int i=1;i<=t;i++)
	{
		int u=path[i];P=0.5;
		for(int j=nxt(i);j!=i;j=nxt(j))
		{
			int v=path[j];
			if(nxt(j)==i) up[u]+=P*(disl[j]+down[v]);
			else up[u]+=P*((down[v]*son[v])/(son[v]+1)+disl[j]);
			P=P/(son[v]+1);
		}
		P=0.5;
		for(int j=pre(i);j!=i;j=pre(j))
		{
			int v=path[j];
			if(pre(j)==i) up[u]+=P*(disr[j]+down[v]);
			else up[u]+=P*((down[v]*son[v])/(son[v]+1)+disr[j]);
			P=P/(son[v]+1);
		}
		for(int j=0;j<tot[u];j++) {
			int v=q[u][j].v;if(vis[v]) continue;
			make_up(v,u,q[u][j].w);
		}
	}
}

统计答案

由于每个点作为起点的概率都相同，那我们就需要统计每个点所有可能情况的期望，最后加起来除以总点数。
设答案为 \(ans\),则有

\[{\Large ans=\frac{1}{n}\sum_u{\frac{son_u \cdot down_u+up_u \cdot fa_u}{son_u+fa_u}}} \]

时间复杂度

对于时间复杂度的分析是相对简单的。无论什么情况算 \(down\) 是普通 \(O(n)\) 的。
对于基环树，其复杂度由算普通节点的 \(up\) 与算环上节点的 \(up\) 共同决定的。
设环中有 \(w\) 个节点，由于统计环中节点 \(up\) 值的时候，需要把每个环中节点遍历一遍，因此时间复杂度为 \(O(n+w^2)\)
但因为出题人很仁慈，\(w\le50\)，因此这种算法随便过（看讨论区有无视 \(w\) 大小严格 \(O(n)\) 的神秘做法，但我不会）

总code

点击查看代码

#include<bits/stdc++.h>
using namespace std;
typedef double ld;
typedef long long ll;
const long long N=2e5;
int n,m,t=0,son[N],fa[N],pos,dfn[N],path[N],tot[N];  
//pos->one point in the circle
ld down[N],up[N],disl[N],disr[N],P;
bool vis[N],flag;  
ld ans=0;
//vis->if the point is in the circle
struct node
{
	int v;ld w;
};
vector <node> q[N];
void add(int u,int v,ld w)
{
	q[u].push_back({v,w}),tot[u]++;
	q[v].push_back({u,w}),tot[v]++;
}
void dfs1(int u,int k)
{
	vis[u]=1;
	for(int i=0;i<tot[u];i++){
		int v=q[u][i].v;if(v==k) continue;
		if(vis[v]) {pos=v;return;}
		dfs1(v,u);
		if(!flag&&pos) {if(pos==u)flag=1;return;}
		if(flag) break;
	}
	vis[u]=0;
}
void dfs2(int u,int k)
{
	dfn[u]=++t;path[t]=u;fa[u]=2;
	for(int i=0;i<tot[u];i++)
	{
		int v=q[u][i].v;if(v==k) continue;
		if(vis[v]) {
			if(!dfn[v]) dfs2(v,u);
			disr[dfn[u]]=disl[dfn[v]]=q[u][i].w;break;
		}
	}
}
void make_down(int u,int k)
{
	for(int i=0;i<tot[u];i++)
	{
		int v=q[u][i].v;if(vis[v]||v==k) continue;
		fa[v]=1;make_down(v,u);son[u]++;down[u]+=1.0*(down[v]+q[u][i].w);
	}
	if(son[u]) down[u]=down[u]/son[u];
}
void make_up(int u,int k,ld w)
{
	up[u]=w;
	if(fa[k]+son[k]-1)
	up[u]=up[u]+(up[k]*fa[k]+down[k]*son[k]-down[u]-w)/(son[k]+fa[k]-1);
	for(int i=0;i<tot[u];i++){
		int v=q[u][i].v;if(v==k||vis[v]) continue;
		make_up(v,u,q[u][i].w);
	}
}
void work1()
{
	make_down(1,0);
	for(int i=0;i<tot[1];i++) make_up(q[1][i].v,1,q[1][i].w);
}
#define nxt(x) (x==t?1:x+1)
#define pre(x) (x==1?t:x-1)
void work2()
{
	dfs1(1,0);
	dfs2(pos,0);
	for(int i=1;i<=t;i++) make_down(path[i],0);
	for(int i=1;i<=t;i++)
	{
		int u=path[i];P=0.5;
		for(int j=nxt(i);j!=i;j=nxt(j))
		{
			int v=path[j];
			if(nxt(j)==i) up[u]+=P*(disl[j]+down[v]);
			else up[u]+=P*((down[v]*son[v])/(son[v]+1)+disl[j]);
			P=P/(son[v]+1);
		}
		P=0.5;
		for(int j=pre(i);j!=i;j=pre(j))
		{
			int v=path[j];
			if(pre(j)==i) up[u]+=P*(disr[j]+down[v]);
			else up[u]+=P*((down[v]*son[v])/(son[v]+1)+disr[j]);
			P=P/(son[v]+1);
		}
		for(int j=0;j<tot[u];j++) {
			int v=q[u][j].v;if(vis[v]) continue;
			make_up(v,u,q[u][j].w);
		}
	}
}
signed main()
{
//	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1,u,v;i<=m;i++){
		ld w;cin>>u>>v>>w;add(u,v,w);
	}
	if(m==n) work2();
	else work1();
	for(int i=1;i<=n;i++) ans+=(down[i]*son[i]+up[i]*fa[i])/(son[i]+fa[i]);
	ans=1.0*(ans/(1.0*n));
	printf("%.5lf",ans);
	return 0;
}

最后特别感谢一下 @emptysetvvvv，题解提供了很多思路讲的也很清楚，也学了一下代码风格

P5298 [PKUWC2018] Minimax

题意：
给定一颗有根二叉树，每个叶子节点有互不相同的权值。
对于每个非叶子节点，都有一个值 \(P_i\) 代表有 \(P_i\) 的概率选择两个儿子中的较大值，有 \(1-P_i\) 的概率选较小值。
假设 \(1\) 号结点的权值有 \(m\) 种可能性，权值第 \(i\) 小的可能性的权值是 \(V_i\)，它的概率为 \(D_i(D_i>0)\)，求：

\[{\Large \sum_{i=1}^{m}i\cdot V_i\cdot D_i^2} \]

\(1\leq n\leq 3\times 10^5\)，\(1\leq w_i\leq 10^9\)。
答案对998244353取模

状态与方程

发现要求的答案由于有平方，并不好直接转移。因为显然每种权值都可能被取到，因此考虑对于每个节点维护每种值被取到的概率
这时状态就比较好做了，其概率显然由其儿子节点转移而来。设对于一个非叶子节点 \(i\)，其权值取为 \(j\) 的概率为 \(f_{i,j}\)，其左右儿子分别为 \(l,r\) 则有

\[{\large f_{i,j}=f_{l,j}(P_i\sum_{k=1}^{j-1}f_{r,k}+(1-P_i)\sum_{k=j+1}^mf_{r,k})+f_{r,j}((1-P_i)\sum_{k=1}^{j-1}f_{l,k}+P_i\sum_{k=j+1}^mf_{l,k}) } \]

转移

现在来考虑如何维护这个东西。由于对于每一个节点都需要维护一个序列，因此显然用线段树来维护。那如何来转移呢？
由于每一个节点都是由其儿子节点转移而来的，每个节点的值又是由左右儿子的前缀和以及其值相乘算出来的，因此是一道典型的线段树合并的题目。
想一下线段树合并的细节。由于线段树合并的过程其实相当暴力，对于几乎每个节点都有涉及，因此考虑直接在逐层向下的时候动态计算前缀和。
又因为合并必须是动态开点的，因此两颗线段树合并的时候可能有一颗线段树有些节点没有而另一颗有。
因此当合并到有一颗线段树没有节点时，就可以加一个区间乘法的tag（毕竟前缀和，当另一颗线段树已经没有值之后前缀和的值也不会变动了，因此直接区间乘法就行）

merge代码

int merge(int x,int y,int l,int r,ll dx,ll dy,ll pp)
{
	if(!x||!y){update(x|y,x?dx:dy);return x|y;}
	int mid=(l+r)>>1;push_down(x),push_down(y);
	int lsx=tr[x].ls,rsx=tr[x].rs,lsy=tr[y].ls,rsy=tr[y].rs;
	ll lsdx=tr[lsx].d,rsdx=tr[rsx].d,lsdy=tr[lsy].d,rsdy=tr[rsy].d;
	tr[x].ls=merge(lsx,lsy,l,mid,(dx+rsdy*(p+1-pp)+p)%p,(dy+rsdx*(p+1-pp)+p)%p,pp);
	tr[x].rs=merge(rsx,rsy,mid+1,r,(dx+lsdy*pp%p+p)%p,(dy+lsdx*pp+p)%p,pp);
	push_up(x);return x;
}

小细节

因为线段树合并需要的空间复杂度是巨大的，因此实际上在合并的时候，所有非叶子节点的线段树的所有节点都是由叶子节点继承而来的。
而叶子节点有 \(n\) 个，又因为动态开点，每个叶子节点的线段树大小是 \(logn\) 的，因此实际上空间复杂度做到了 \(nlogn\)
不过需要注意的是，由于是值域线段树，因此上述复杂度分析中的 \(n\) 实际上指的是值域，但值域范围巨大（\(1e9\)），因此需要离散化。

code

点击查看代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll p=998244353;
const ll N=3e5+7;
const ll ni=796898467;
ll n,son[N][3],tot[N],d[N],val[N],cntt,idcnt=0;
int rt[N];
struct node
{
	ll d,tag;int ls=0,rs=0;
}tr[N<<6];
inline int jia(int x, int y){return x - p + y >= 0 ? x - p + y : x + y;}
void push_up(int u){tr[u].d=jia(tr[tr[u].ls].d,tr[tr[u].rs].d);}
void update(int u,ll w)
{
	if(!u) return;
	tr[u].d=tr[u].d*w%p;
	tr[u].tag=tr[u].tag*w%p;
}
void push_down(int u)
{
	if(tr[u].tag==1) return;
	update(tr[u].ls,tr[u].tag),update(tr[u].rs,tr[u].tag);
	tr[u].tag=1;return;
}
void build(int &u,int l,int r,int x)
{
	if(!u) u=++idcnt,tr[u].tag=1;
	if(l==r){tr[u].d=1ll;return;}
	int mid=(l+r)/2;
	if(x<=mid) build(tr[u].ls,l,mid,x);
	else build(tr[u].rs,mid+1,r,x);
	push_up(u);
}
int merge(int x,int y,int l,int r,ll dx,ll dy,ll pp)
{
	if(!x||!y){update(x|y,x?dx:dy);return x|y;}
	int mid=(l+r)>>1;push_down(x),push_down(y);
	int lsx=tr[x].ls,rsx=tr[x].rs,lsy=tr[y].ls,rsy=tr[y].rs;
	ll lsdx=tr[lsx].d,rsdx=tr[rsx].d,lsdy=tr[lsy].d,rsdy=tr[rsy].d;
	tr[x].ls=merge(lsx,lsy,l,mid,(dx+rsdy*(p+1-pp)+p)%p,(dy+rsdx*(p+1-pp)+p)%p,pp);
	tr[x].rs=merge(rsx,rsy,mid+1,r,(dx+lsdy*pp%p+p)%p,(dy+lsdx*pp+p)%p,pp);
	push_up(x);return x;
}
void dfs(int u)
{
	if(tot[u]==0) build(rt[u],1,cntt,d[u]);//d_u ->the value of the point
	if(tot[u]==1)dfs(son[u][0]),rt[u]=rt[son[u][0]];
	if(tot[u]==2)
	dfs(son[u][0]),dfs(son[u][1]),rt[u]=merge(rt[son[u][0]],rt[son[u][1]],1,cntt,0,0,d[u]);
}
ll f[N];
void getans(int u,int l,int r)
{
	if(!u) return;
	if(l==r) {f[l]=tr[u].d;return;}
	int mid=(l+r)>>1;push_down(u);
	getans(tr[u].ls,l,mid),getans(tr[u].rs,mid+1,r);
}
int main()
{
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++) {ll x;cin>>x;if(x==0) continue;son[x][tot[x]++]=i;}
	cntt=0;
	for(int i=1;i<=n;i++) 
	{
		cin>>d[i];
		if(!tot[i]) val[++cntt]=d[i];
		else d[i]=d[i]*ni%p;
	}sort(val+1,val+cntt+1);
	for(int i=1;i<=n;i++) if(!tot[i]) d[i]=lower_bound(val+1,val+cntt+1,d[i])-val;
	dfs(1);getans(rt[1],1,cntt);ll ans=0;
	for(int i=1;i<=cntt;i++) ans=(ans+1ll*i*val[i]%p*f[i]%p*f[i]%p+p)%p;
	cout<<ans<<'\n';
	return 0;
}

posted @ 2024-10-23 12:01 all_for_god 阅读(39) 评论(0) 收藏举报

刷新页面返回顶部

allforgod

概率DP

P2081 [NOI2012] 迷失游乐园

普通树

普通树code

基环树

非环上节点

环上节点

基环树code

统计答案

时间复杂度

总code

P5298 [PKUWC2018] Minimax

状态与方程

转移

小细节

code

公告