FHQ treap(无旋treap)
平衡树作为一种中级数据结构,有着广泛的使用场景。其平衡性的维护方式灵活多变,而其中的无旋treap更以简单著称
P3369 【模板】普通平衡树
给定集合。
修改:
插入一个数 x。
删除一个数 x(若有多个相同的数,应只删除一个)。
查询:
定义排名为比当前数小的数的个数 +1。查询 x 的排名。
查询数据结构中排名为 x 的数。
求 x 的前驱(前驱定义为小于 x,且最大的数)。
求 x 的后继(后继定义为大于 x,且最小的数)。
定义
平衡树是一种二叉搜索树,而treap将其与堆结合,使其同时具有二者的性质。
treap通过给每个节点一个随机数值,依靠这个值维护一个堆,保证树的平衡性。
而无旋treap通过两种关键操作来维护这两者的性质:split和merge
split
split将目标树按值分裂成两棵树,由于分裂后需要返回两颗树的根,不好返回,因此用指针&x和&y来传递分裂后的两个根
由于二叉搜索树的性质:u左子树的节点值都比u的权值小,而右子树的都比u的大。因此如果分裂目标k比u小,那么就去左子树找
反之亦然
由于二叉搜索树的性质,分裂出来的x子树中的所有值都比y子树中的所有值小。这个性质在合并时非常关键
#define ls (tr[u].l)
#define rs (tr[u].r)
void push_up(int u)
{
tr[u].size=1+tr[ls].siz+tr[rs].siz;
}
void split(int u,int &x,int &y,int k)
{
if(u==0){x=0,y=0;return;}
if(tr[u].val<=k)
{
x=u,split(rs,rs,y,k);
}
else y=u,split(ls,x,ls,k);
push_up(u);
}
容易理解,split并不破坏原treap堆的性质
注意 代码中关于&x与&y的确定需要特别强调。x代表分裂出来权值较小的子树的根节点,y代表分裂出来权值较大的子树的根节点,如下图
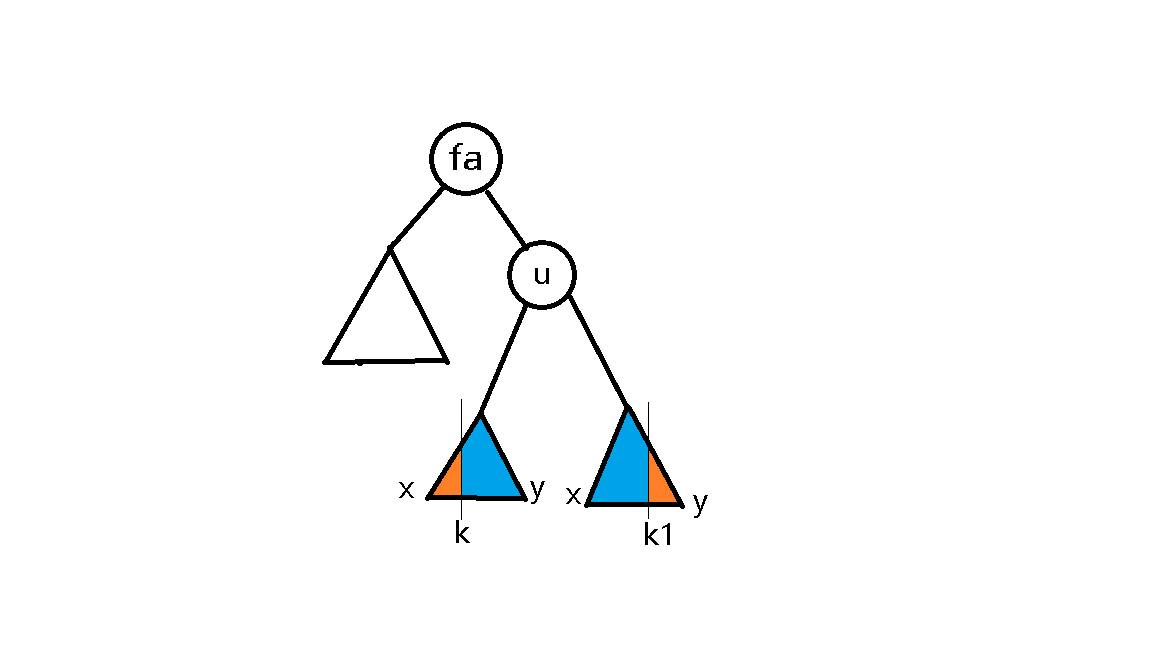
如果k比u的值大,证明整个左子树都比k小,因此这时的k就在k1的位置上。
因此u及其子树k1左边的全是属于其父亲给出的x,即分裂出的较小的子树。而较大的子树还不知道,就到k1右边的橙色部分中找
而将u的右子树带到split函数中x的位置,是为了更新u的右子树,在分裂完成后将剩下的小于k的部分接回u右子树的空缺
这个过程中,左子树无影响。分裂完后,u的大小很可能改变,因此要push_up更新大小
而k在图中左边的原理同理,不再赘述。
merge
merge是将两个二叉平衡树合并的函数,要求以x为根的子树中所有元素都必须小于y子树中的元素。这个要求看似苛刻,但正好与split出来的子树的性质不谋而合。
由于合并的两棵树x中所有值都比y小,因此对于二叉搜索树的性质,只需要将大的树接在小的树右下角或者小的接在大的左下角就行了。
merge的关键是一个随机值:\(tr[u].rnd\) 。还记得前文说到treap是二叉搜索树与堆的结合吗?split并不破坏堆的性质,而merge正好就根据初始所附的随机值来维护堆的性质。如何维护具体看代码
int merge(int x,int y) //返回的是两树合并后的根节点
{
if(!x||!y) return x+y; //如果x或y中任意一一个为零,就直接以另一个为根
if(tr[x].rnd<tr[y].rnd) //维护的是小根堆。若x的随机值比y的小,那么x就在y上面,x作为根被返回
{
tr[x].r=merge(tr[x].r,y);push_up(x);return x;
}
else
{
tr[y].l=merge(x,tr[y].l);push_up(y);return y;//否则y当根,注意merge中带入的第一棵树值都比第二颗小
}
}
具体操作
讲了这么多,实际上与开头具体的操作关系并不大。现在,就看看如何用以上两个函数实现这些操作
- 插入
先新建一个节点,再按这个点的值进行分裂。这时,其中一个子树中所有值都小于等于新建节点的值。依次合并回去就好了
mt19937 myrand(time(0));
int newnode(int val)
{
int u=++cnt;
tr[u].siz=1,tr[u].val=val,tr[u].l=tr[u].r=0,tr[u].rnd=myrand();
return u;
}
int u=newnode(x);//x是输入进来的权值
int lrt,rrt;
split(root,lrt,rrt,x);
root=merge(merge(lrt,u),rrt);//注意合并时都要给root重新赋值
- 删除
按x-1、x、x+1分裂成3个树,中间那个树所有权值都是x了。但注意不能将整个树全部扔掉。直接将中间树根节点的左右儿子合并即可。
int lr,mr,rr;
split(root,lr,rr,x-1);split(rr,mr,rr,x+1);
mr=merge(tr[mr].l,tr[mr].r);
root=merge(merge(lr,mr),rr);
- 查找x的排名
按x-1分裂,直接输出较小的树的siz即可
int lr,rr;
split(root,lr,rr,x-1);
printf("%d\n",tr[lr].siz+1);
root=merge(lr,rr);
- 查找排名为x的数
根据二叉搜索树的性质直接找
int kth(int u,int k)
{
int lsiz=tr[ls].size;
if(lsiz+1==k) return u;
if(lsiz+1>k) return kth(ls,k);
else return kth(rs,k-lsiz-1);
}
printf("%d\n",tr[kth(root,x)].val);
- 求x的前驱
仍然利用kth函数,将root按x-1分裂成两个树,再找较小子树中最大的数
int lr,rr;
split(root,lr,rr,x-1);
printf("%d\n",tr[kth(lr,tr[lr].siz)].val);
root=merge(lr,rr);
- 求x的后继
几乎同上,按x+1分裂,找较大子树中最小的数
int lr,rr;
split(root,lr,rr,x+1);
printf("%d\n",tr[kth(rr,1)].val);
root=merge(lr,rr);
以上,就是普通平衡树的全部操作。
P4309 [TJOI2013] 最长上升子序列
修改:每次向序列中插入当前最大值。查询:每个时刻的最长上升子序列。
比较简单。由于每次插入的是最大值,因此直接求前缀最大值加 1 即当前位置的答案。
注意,由于这个地方是序列上的平衡树,因此 split 操作是依据 siz 而不是权值,merge 保证的也是 \(x\) 中的所有值都在 \(y\) 右边且 \(x\) 与 \(y\) 相邻。
code
点击查看代码
#include<bits/stdc++.h>
bool Mbe;
using namespace std;
#define ll long long
//namespace FIO{
// template<typename P>
// inline void read(P &x){P res=0,f=1;char ch=getchar();while(ch<'0' || ch>'9'){if(ch=='-') f=-1;ch=getchar();}while(ch>='0' && ch<='9'){res=(res<<3)+(res<<1)+(ch^48);ch=getchar();}x=res*f;}
// template<typename Ty,typename ...Args>
// inline void read(Ty &x,Args &...args) {read(x);read(args...);}
// inline void write(ll x) {if(x<0ll)putchar('-'),x=-x;static int sta[35];int top = 0;do {sta[top++] = x % 10ll, x /= 10ll;} while (x);while (top) putchar(sta[--top] + 48);}
//}
//using FIO::read;using FIO::write;
const int N=1e5+7;
mt19937 rnd(time(0));
int ans=0;
namespace fhq{
int idcnt=0;
struct node{int l,r,w,mx,siz;unsigned int rd;}tr[N];
#define ls (tr[u].l)
#define rs (tr[u].r)
void push_up(int u){tr[u].mx=max({tr[u].w,tr[ls].mx,tr[rs].mx});tr[u].siz=tr[ls].siz+tr[rs].siz+1;}
int get(int w){tr[++idcnt]={0,0,w,w,1,rnd()};return idcnt;}
void split(int u,int &x,int &y,int k){
if(!u){x=y=0;return;}
if(!k){y=u,x=0;return;}
if(tr[ls].siz>=k){y=u;split(ls,x,ls,k);}
else{x=u;split(rs,rs,y,k-tr[ls].siz-1);}
push_up(u);
}
int merge(int x,int y){
if(!x||!y){return x+y;}
if(tr[x].rd<tr[y].rd){tr[x].r=merge(tr[x].r,y);push_up(x);return x;}
else {tr[y].l=merge(x,tr[y].l);push_up(y);return y;}
}
}
int n,rt;
bool Med;
signed main(){
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
cin>>n;
for(int i=1;i<=n;i++){
int loc;cin>>loc;int x,y,w;fhq::split(rt,x,y,loc);w=fhq::tr[x].mx+1;
rt=fhq::merge(fhq::merge(x,fhq::get(w)),y);
ans=max(ans,w);cout<<ans<<'\n';
}
cerr<<'\n'<<1e3*clock()/CLOCKS_PER_SEC<<"ms\n";
cerr<<'\n'<<fabs(&Med-&Mbe)/1048576.0<<"MB\n";
return 0;
}
P3215 [HNOI2011] 括号修复 / [JSOI2011] 括号序列
给定括号序列。修改:区间覆盖,翻转,反转。查询:区间如果能够成为合法括号序列至少要单点修改多少次。
发现修改都是平衡树经典修改,考虑查询怎么做。
考虑判断括号序列合法的题都是找在当前序列下一个括号序列合法的充要条件。一般而言都是形如一直删去合法的括号序列的方式。
考虑这道题只有一种括号,因此删完之后一定形如 ))))(((( 的形式。设删完后有 \(x\) 个左括号,\(y\) 个右括号,那么改 $\left \lceil \frac x 2 \right \rceil + \left \lceil \frac y 2 \right \rceil $ 个即可,证明比较显然。
我们将左括号看作 -1,将右括号看作 1,那么 \(x\) 就等于前缀最小值,\(y\) 就等于后缀最大值。由于有反转翻转操作因此维护前后缀最大最小值即可。
code
说起来容易写起来难受。注意标记的下传顺序是反转,覆盖,翻转,以及标记之间的影响。其他就没什么了。
点击查看代码
#include<bits/stdc++.h>
bool Mbe;
using namespace std;
#define ll long long
//namespace FIO{
// template<typename P>
// inline void read(P &x){P res=0,f=1;char ch=getchar();while(ch<'0' || ch>'9'){if(ch=='-') f=-1;ch=getchar();}while(ch>='0' && ch<='9'){res=(res<<3)+(res<<1)+(ch^48);ch=getchar();}x=res*f;}
// template<typename Ty,typename ...Args>
// inline void read(Ty &x,Args &...args) {read(x);read(args...);}
// inline void write(ll x) {if(x<0ll)putchar('-'),x=-x;static int sta[35];int top = 0;do {sta[top++] = x % 10ll, x /= 10ll;} while (x);while (top) putchar(sta[--top] + 48);}
//}
//using FIO::read;using FIO::write;
const int N=1e5+7,inf=2e8+7;
mt19937 rnd(time(0));
namespace fhq{
int idcnt=0,rt=0;
struct node{int l,r,w,s,pre1,pre2,suf1,suf2,t1,t2,t3,siz;unsigned int rk;}tr[N]; //1 mi 2 mx //覆盖,翻转,反转,可以最先覆盖然后清空反转与翻转标记
#define ls (tr[u].l)
#define rs (tr[u].r)
int get(int w){int u=++idcnt;if(w==1){tr[u]={0,0,w,w,0,1,0,1,0,0,0,1,rnd()};}else{tr[u]={0,0,w,w,-1,0,-1,0,0,0,0,1,rnd()};}return u;}
void init(){memset(tr,0,sizeof(tr));}
void push_up(int u){
if(!u)return;
tr[u].s=tr[ls].s+tr[rs].s+tr[u].w;tr[u].siz=tr[ls].siz+tr[rs].siz+1;
tr[u].pre1=min({tr[ls].pre1,tr[ls].s+tr[rs].pre1+tr[u].w});tr[u].pre2=max({tr[ls].pre2,tr[ls].s+tr[rs].pre2+tr[u].w});
tr[u].suf1=min({tr[rs].suf1,tr[rs].s+tr[ls].suf1+tr[u].w});tr[u].suf2=max({tr[rs].suf2,tr[rs].s+tr[ls].suf2+tr[u].w});
}
void upd(int u,int t1,int t2,int t3){
if(!u)return;
if(t3){
tr[u].w=-tr[u].w;tr[u].s=-tr[u].s;
swap(tr[u].pre1,tr[u].pre2),swap(tr[u].suf1,tr[u].suf2);
tr[u].pre1=-tr[u].pre1,tr[u].pre2=-tr[u].pre2;
tr[u].suf1=-tr[u].suf1,tr[u].suf2=-tr[u].suf2;
tr[u].t3^=1;tr[u].t1=-tr[u].t1;
}
if(t1!=0){
tr[u].w=tr[u].t1=t1;tr[u].s=t1*tr[u].siz;
if(t1==-1)tr[u].pre1=tr[u].suf1=-tr[u].siz,tr[u].pre2=tr[u].suf2=0;
else tr[u].pre1=tr[u].suf1=0,tr[u].pre2=tr[u].suf2=tr[u].siz;
}
if(t2){
swap(tr[u].pre1,tr[u].suf1),swap(tr[u].pre2,tr[u].suf2);
swap(ls,rs);tr[u].t2^=1;
}
}
void push_down(int u){
if(!u)return;
upd(ls,tr[u].t1,tr[u].t2,tr[u].t3);
upd(rs,tr[u].t1,tr[u].t2,tr[u].t3);
tr[u].t1=tr[u].t2=tr[u].t3=0;
}
void split(int u,int &x,int &y,int k){
if(!u){x=y=0;return;}
if(!k){y=u,x=0;return;}
push_down(u);
if(tr[ls].siz>=k){y=u;split(ls,x,ls,k);}
else {x=u;split(rs,rs,y,k-tr[ls].siz-1);}
push_up(u);
}
int merge(int x,int y){
if(!x||!y){return x+y;}
push_down(x),push_down(y);
if(tr[x].rk<tr[y].rk){tr[x].r=merge(tr[x].r,y);push_up(x);return x;}
else{tr[y].l=merge(x,tr[y].l);push_up(y);return y;}
}
#undef ls
#undef rs
void split_reg(int l,int r,int &x,int &y,int &z){split(rt,x,z,r);int xx=x;split(xx,x,y,l-1);} //y 是目标树
void merge_reg(int x,int y,int z){rt=merge(merge(x,y),z);}
void push(int w){rt=merge(rt,get(w));}
void Replace(int l,int r,int w){int x,y,z;split_reg(l,r,x,y,z);upd(y,w,0,0);merge_reg(x,y,z);}
void Swap(int l,int r){int x,y,z;split_reg(l,r,x,y,z);upd(y,0,1,0);merge_reg(x,y,z);}
void Invert(int l,int r){int x,y,z;split_reg(l,r,x,y,z);upd(y,0,0,1);merge_reg(x,y,z);}
int Query(int l,int r){int x,y,z;split_reg(l,r,x,y,z);int ans=((-tr[y].pre1)+1)/2+(tr[y].suf2+1)/2;merge_reg(x,y,z);return ans;}
}
int n,m;
bool Med;
signed main(){
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
cin>>n>>m;fhq::init();
for(int i=1,w;i<=n;i++){char x;cin>>x;w=(x==')')?-1:1;fhq::push(w);}
for(int i=1,l,r,w;i<=m;i++){
string op;char x;cin>>op>>l>>r;
if(op[0]=='R'){cin>>x;w=(x==')')?-1:1;fhq::Replace(l,r,w);}
if(op[0]=='S'){fhq::Swap(l,r);}
if(op[0]=='I'){fhq::Invert(l,r);}
if(op[0]=='Q'){cout<<fhq::Query(l,r)<<'\n';}
}
// cerr<<'\n'<<1e3*clock()/CLOCKS_PER_SEC<<"ms\n";
// cerr<<'\n'<<fabs(&Med-&Mbe)/1048576.0<<"MB\n";
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号