从逻辑回归开始
假设函数
\[h_{\theta}(x)=\frac{1}{1+e^{-\theta^Tx}}
\]
其中
\[\theta=\begin{bmatrix}\theta_0 \\ \theta_1 \\ \dots \\\theta_n \end{bmatrix},\ \
x=\begin{bmatrix}x_0 \\ x_1 \\ \dots \\x_n \end{bmatrix}
\]
这里的\(\theta_i\)是一系列估计的参数,\(x_i\)是样本的特征,特别地,\(x_0=0\)
对于正样本(\(y=1\)),希望\(h_{\theta}(x)\)尽可能接近\(1\),因此需要\(\theta^Tx\gg0\),
对于负样本(\(y=0\)),希望\(h_{\theta}(x)\)尽可能接近\(0\),因此需要\(\theta^Tx\ll0\)。
但是只要正样本\(\theta^Tx\ge0\),负样本\(\theta^Tx<0\)就可以做到正确分类。
代价函数(含正则化项)
\[J(\theta)=\frac1m \sum_{i=1}^m(y^{(i)}(-\log \frac{1}{1+e^{-\theta^Tx}})+(1-y^{(i)})(-\log(1-\frac{1}{1+e^{-\theta^Tx}})))+\frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2
\]
这里\(n\)为特征数,\(m\)为样本数,下同
SVM:大间隔分类——Large margin classification
SVM代价函数
\[J(\theta)=C\sum_{i=1}^m(y^{(i)}cost_1(\theta^Tx^{(i)})+(1-y^{(i)})cost_0(\theta^Tx^{(i)}))+\frac12\sum_{i=1}^n\theta_j^2
\]
其中\(cost_0()\)和\(cost_1()\)为铰链损失函数(Hinge loss),形状如下(直接抄了老师的图)
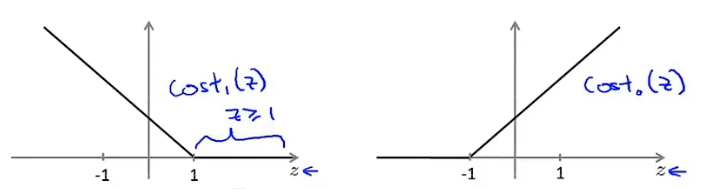
对于SVM的参数\(\theta\)有更高的要求,恰好能正确分类是不够的。因此希望有合适的参数\(\theta\)使得对于正样本(\(y=1\)),需要\(\theta^Tx\ge 1\),对于负样本(\(y=0\)),需要\(\theta^Tx\le-1\)(相当于在SVM构建安全距离)。

上图中绿色和紫红色超平面虽然能够做到正确的分类,但是它们距离两类样本的间隔过小,并不是良好的决策超平面。黑色超平面与两类样本都有较大的间距(Margin),是比较好的决策超平面。设图中\(\circ\)为正样本,\(\times\)为负样本,\(n=2\),则图中截距较小的蓝色超平面为负超平面:\(\theta^Tx=\theta_0x_0+\theta_1x_1+\theta_2x_2=-1\),另一超平面为正超平面:\(\theta^Tx=\theta_0x_0+\theta_1x_1+\theta_2x_2=1\)。为了获得良好的分类效果,我们需要将SVM的间隔最大化。先在正负超平面上各选取一个支持向量点,设这两个样本为\(p,q.\)
由于\(x_0=1\),两式可写为:
\[\begin{aligned}
\theta_0+\theta_1x_1^p+\theta_2x_2^p&=1\quad\quad &①\\
\theta_0+\theta_1x_1^q+\theta_2x_2^q&=-1\quad\quad &②
\end{aligned}
\]
然后将\(①\)式减去\(②\)式:
\[0\cdot \theta_0+\theta_1(x_1^p-x_1^q)+\theta_2(x_2^p-x_2^q)=2\\
\]
将上式描述成向量内积形式,\(\vec{x^p}\)和\(\vec{x^q}\)是原点指向样本\(p,q\)的向量(支持向量)
\[\vec\theta\cdot (\vec{x^p}-\vec{x^q})=2\quad\quad ③
\]
在决策边界任选不同的两点\(r,s\),满足:
\[\begin{aligned}
\theta^Tx^r &=0\quad\quad ④\\
\theta^Tx^s &=0\quad\quad ⑤
\end{aligned}
\]
\(④\)式减\(⑤\)式可得:
\[\vec{\theta}(\vec{x^r}-\vec{x^s})=0\quad\quad ⑥
\]
由内积性质可知向量\(\theta\)与决策超平面垂直,同样可以将③式改写:
\[\parallel \vec{x^p}-\vec{x^q}\parallel\cdot\cos{\phi}\cdot\parallel\vec\theta\parallel=2\quad\quad③'
\]
其中\(\parallel \vec{x^p}-\vec{x^q}\parallel\cdot\cos{\phi}\)即向量\(\vec{x^p}-\vec{x^q}\)在\(\vec{\theta}\)方向上的投影,同时也是SVM的间隔
设SVM间隔为\(L\),由\(③'\)可以推出\(L\)的表达式:
\[\begin{aligned}
L&=\parallel \vec{x^p}-\vec{x^q}\parallel\cdot\cos{\phi}\\
&=\frac{2}{\parallel\vec\theta\parallel}
\end{aligned}
\]
要使得\(L\)最大,等价于求解向量\(\vec\theta\)长度的最小化问题;由于\(\parallel \theta \parallel=\sqrt{\sum_{i=0}^n\theta_i^2}\)不好计算,将优化的目标函数改为
\[f(\theta)=\frac{\parallel\theta\parallel^2}{2}
\]
所有正样本位于正超平面上方,满足不等式约束
\[\begin{aligned}
\theta^Tx^{(i)}=&\ge 1\\
\end{aligned}
\]
所有负样本位于负超平面下方,满足不等式约束
\[\begin{aligned}
\theta^Tx^{(i)}&\le -1\\
\end{aligned}
\]
现令负样本标签\(y_i=-1\),约束条件变为:
\[y^{(i)}(\theta^Tx^{(i)})\ge1
\]
那么问题可以描述为带KKT条件(含不等式约束)的最优化问题:
\[\begin{aligned}
\min \quad &f(\theta)\\
{\mathbf s.t. \quad }&y^{(i)}(\theta^Tx^{(i)})-1\ge 0
\end{aligned}
\]
可以再添加一个变量\(a_i(a_i\ge 0)\)将不等式约束变为等式约束:
\[\begin{aligned}
\min \quad &f(\theta)\\
{\mathbf s.t.} \quad &y^{(i)}(\theta^Tx^{(i)})-1-a_i^2=0
\end{aligned}
\]
然后可以使用拉格朗日乘数法求解(\(\lambda,\theta,a\)为向量,带下标的为它的分量):
\[L(\vec\theta,\vec\lambda,\vec a)=\frac{\parallel \vec\theta\parallel^2}
{2}-\sum_{i=1}^m\lambda_i(y^{(i)}\theta^Tx^{(i)}-1-a_i^2)
\]
\[\left\{
\begin{aligned}
\frac{\partial L}{\partial \theta} & = \vec \theta -\sum_{i=1}^m\lambda_iy^{(i)}x^{(i)} &=\vec0\quad \\
\frac{\partial L}{\partial \lambda_i} & =y^{(i)}\theta^Tx^{(i)}-1-a_i^2 &=0\quad \\
\frac{\partial L}{\partial a_i} & = 2\lambda_ia_i &=0\quad
\end{aligned}
\right.
\]



 浙公网安备 33010602011771号
浙公网安备 33010602011771号