数据结构|《啊哈!算法》读书笔记
第一章:排序
本章主要介绍了几种常见的排序算法,其中快速排序较难理解,代码实现也比较复杂。
简化版桶排序
本章介绍的是简化版的桶排序,后继会介绍真正的桶排序。
简单桶排序原理图:
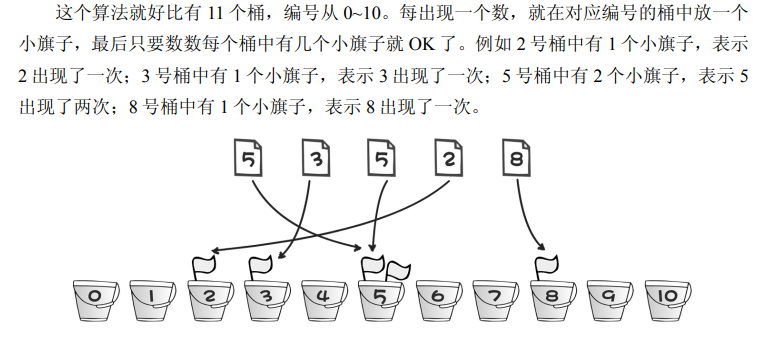
C语言实现(本例排序0-1000的整数):
#include <stdio.h>
int main()
{
int book[1001],i,j,t,n;
for(i=0;i<=1000;i++)
book[i]=0;
scanf("%d",&n);//输入一个数n,表示接下来有n个数
for(i=1;i<=n;i++)//循环读入n个数,并进行桶排序
{
scanf("%d",&t); //把每一个数读到变量t中
book[t]++; //进行计数,对编号为t的桶放一个小旗子
}
for(i=1000;i>=0;i--) //依次判断编号1000~0的桶
for(j=1;j<=book[i];j++) //出现了几次就将桶的编号打印几次
printf("%d ",i);
getchar();getchar();
return 0;
}
输入数据:
10 8 100 50 22 15 6 1 1000 999 0
运行结果:
1000 999 100 50 22 15 8 6 1 0
冒泡排序
原理:每次比较两个相邻的元素,如果顺序错误则交换
C语言实现:
#include <stdio.h> int main() { int a[100],i,j,t,n; scanf("%d",&n); //输入一个数n,表示接下来有n个数 for(i=1;i<=n;i++) //循环读入n个数到数组a中 scanf("%d",&a[i]); //冒泡排序的核心部分 for(i=1;i<=n-1;i++) //n个数排序,只用进行n-1趟 { for(j=1;j<=n-i;j++) //从第1位开始比较直到最后一个尚未归位的数 { if(a[j]<a[j+1]) //比较大小并交换 { t=a[j]; a[j]=a[j+1]; a[j+1]=t; } } } for(i=1;i<=n;i++) //输出结果 printf("%d ",a[i]); getchar();getchar(); return 0; }
输入结果
10 8 100 50 22 15 6 1 1000 999 0
输出结果
0 1 6 8 15 22 50 100 999 1000
快速排序
快速排序原理:找一个数作为基准数,从两边移动"哨兵"寻找大于该数的数和小于该数的数,不断交换,直到"哨兵"相遇,进行最后一次交换,归位基准数。再对剩余未排序的序列采用分而治之的思想,重复执行上述过程,直到排序完成。
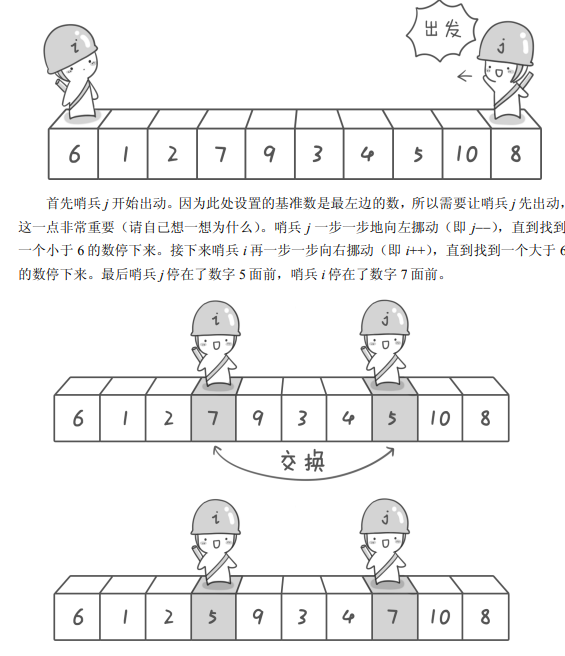
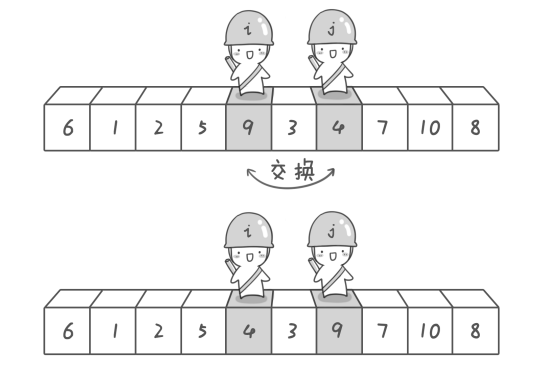
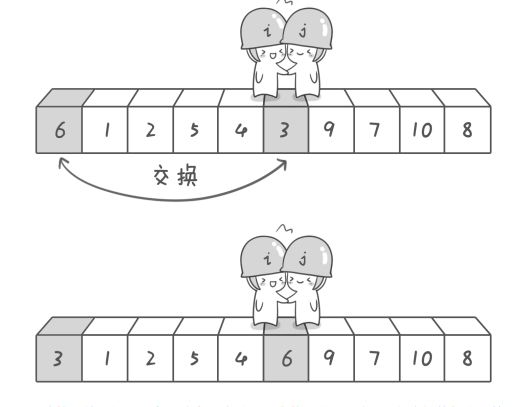
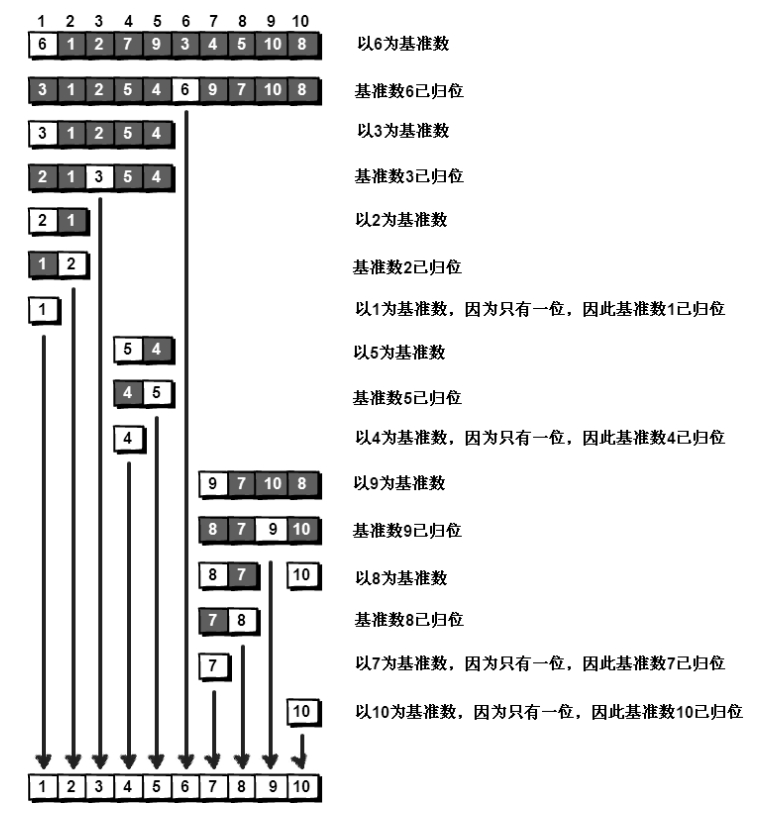
代码实现:(PS:c要自己造轮子,真辛苦!)
1 #include <stdio.h> 2 int a[101],n;//定义全局变量,这两个变量需要在子函数中使用 3 void quicksort(int left,int right) 4 { 5 int i,j,t,temp; 6 if(left>right) 7 return; 8 9 temp=a[left]; //temp中存的就是基准数 10 i=left; 11 j=right; 12 while(i!=j) 13 { 14 //顺序很重要,要先从右往左找 15 while(a[j]>=temp && i<j) 16 j--; 17 //再从左往右找 18 while(a[i]<=temp && i<j) 19 i++; 20 //交换两个数在数组中的位置 21 if(i<j)//当哨兵i和哨兵j没有相遇时 22 { 23 t=a[i]; 24 a[i]=a[j]; 25 a[j]=t; 26 } 27 } 28 //最终将基准数归位 29 a[left]=a[i]; 30 a[i]=temp; 31 32 quicksort(left,i-1);//继续处理左边的,这里是一个递归的过程 33 quicksort(i+1,right);//继续处理右边的,这里是一个递归的过程 34 } 35 int main() 36 { 37 int i,j,t; 38 //读入数据 39 scanf("%d",&n); 40 for(i=1;i<=n;i++) 41 scanf("%d",&a[i]); 42 quicksort(1,n); //快速排序调用 43 44 //输出排序后的结果 45 for(i=1;i<=n;i++) 46 printf("%d ",a[i]); 47 getchar();getchar(); 48 return 0; 49 }
输入结果
10 6 1 2 7 9 3 4 5 10 8
输出结果
1 2 3 4 5 6 7 8 9 10
实例:买书
题目:小哼的学校要建立一个图书角,老师派小哼去找一些同学做调查,看看同学们都喜欢读 哪些书。小哼让每个同学写出一个自己最想读的书的 ISBN 号(你知道吗?每本书都有唯一 的 ISBN 号,不信的话你去找本书翻到背面看看)。当然有一些好书会有很多同学都喜欢, 这样就会收集到很多重复的 ISBN 号。小哼需要去掉其中重复的 ISBN 号,即每个 ISBN 号只 保留一个,也就说同样的书只买一本(学校真是够抠门的)。然后再把这些 ISBN 号从小到 大排序,小哼将按照排序好的 ISBN 号去书店买书。请你协助小哼完成“去重”与“排序” 的工作。 输入有 2 行,第 1 行为一个正整数,表示有 n 个同学参与调查(n≤100)。第 2 行有 n 个用空格隔开的正整数,为每本图书的 ISBN 号(假设图书的 ISBN 号在 1~1000 之间)。 输出也是 2 行,第 1 行为一个正整数 k,表示需要买多少本书。第 2 行为 k 个用空格隔 开的正整数,为从小到大已排好序的需要购买的图书的 ISBN 号。
样例输入:
10 20 40 32 67 40 20 89 300 400 15
样例输出:
8 15 20 32 40 67 89 300 400
分析:两种思路。
思路一:先把n个图书的ISBN号去重,再进行从小到大排序并输出。考虑使用简单桶排序,先把n个图书的ISBN号写入各个桶中,再依次判断各个桶中是否有书.
#include <stdio.h> int main() { int a[1001],n,i,t; for(i=1;i<=1000;i++) a[i]=0; //初始化 int cnt = 0; scanf("%d",&n); //读入n for(i=1;i<=n;i++) //循环读入n个图书的ISBN号 { scanf("%d",&t); //把每一个ISBN号读到变量t中 a[t]=1; //标记出现过的ISBN号 } for(i=1;i<=1000;i++) //依次判断1~1000这个1000个桶 { if(a[i]==1)//如果桶里有书则计数器加1 cnt++; } printf("%d\n",cnt); for(i=1;i<=1000;i++) //依次判断1~1000这个1000个桶 { if(a[i]==1)//如果这个ISBN号出现过则打印出来 printf("%d ",i); } return 0; }
思路二:先从小到大排序,再去重输出。考虑使用快速排序先排序再设立测试条件:如果当前这个数是第一次出现则输出。
注:这串代码有BUG,最后一个数不会被排序,原因不明...
#include <stdio.h> #include <stdlib.h> int cmp(const void *a, const void *b){ return *(int *)a - *(int *)b;//升序 // return *(int *)b - *(int *)a;//降序 } int main() { int a[101],n,i,j,t; scanf("%d",&n); //读入n for(i=1;i<=n;i++) //循环读入n个图书ISBN号 { scanf("%d",&a[i]); } qsort(a, n, sizeof(a[0]), cmp); printf("%d ",a[1]); //输出第1个数 for(i=2;i<=n;i++) //从2循环到n { if( a[i] != a[i-1] ) //如果当前这个数是第一次出现则输出 printf("%d ",a[i]); } getchar();getchar(); return 0; }
第二章:栈、队列、链表
本章栈,队列较好理解,链表较难。
队列
遵循先进先出原则(FIFO)
基本操作
q[tail]=x;//入队 tail++;
head++;//出队
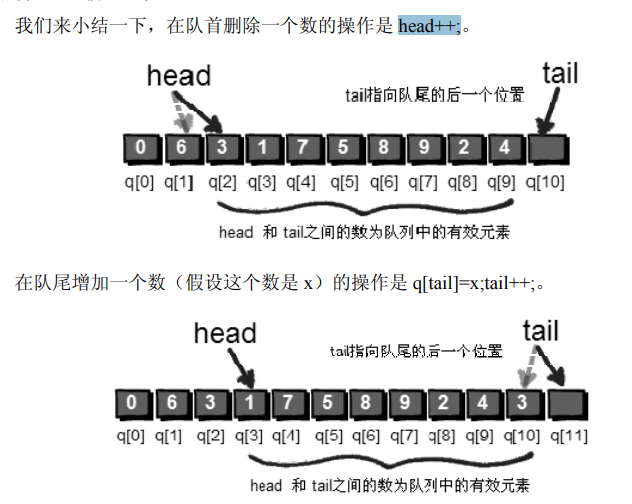
队列结构
struct queue { int data[100];//队列的主体,用来存储内容 int head;//队首 int tail;//队尾 };
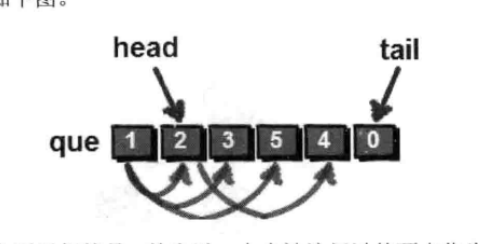
猜谜小游戏
给出一串数字,首先将第 1 个数删除,紧接着将第 2 个数放到 这串数的末尾,再将第 3 个数删除并将第 4 个数放到这串数的末尾,再将第 5 个数删除…… 直到剩下最后一个数,将最后一个数也删除。输出最后所有被删除的数编排的结果。
1 #include <stdio.h> 2 struct queue 3 { 4 int data[100];//队列的主体,用来存储内容 5 int head;//队首 6 int tail;//队尾 7 }; 8 int main() 9 { 10 struct queue q; 11 int i; 12 //初始化队列 13 q.head=1; 14 q.tail=1; 15 for(i=1;i<=9;i++) 16 { 17 //依次向队列插入9个数 18 scanf("%d",&q.data[q.tail]); 19 q.tail++; 20 } 21 22 while(q.head<q.tail) //当队列不为空的时候执行循环 23 { 24 //打印队首并将队首出队 25 printf("%d ",q.data[q.head]); 26 q.head++; 27 28 //先将新队首的数添加到队尾 29 q.data[q.tail]=q.data[q.head]; 30 q.tail++; 31 //再将队首出队 32 q.head++; 33 } 34 35 getchar();getchar(); 36 return 0; 37 }
输入结果
1 2 3 4 5 6 7 8 9
输出结果
1 3 5 7 9 4 8 6 2
栈
基本概念
遵循先进后出原则
struct stack { int data[10]; int top; };
stack s;//创建栈s
s.top = 0;//初始化栈 s.top++; s.data[s.top]=x;//入栈操作 s.top--;//出栈操作
实例:判断回文
输入一串字符串,要求判断是否是回文。
1 #include <stdio.h> 2 #include <string.h> 3 int main() 4 { 5 char a[101],s[101]; 6 int i,len,mid,next,top; 7 8 gets(a); //读入一行字符串 9 len=strlen(a); //求字符串的长度 10 mid=len/2-1; //求字符串的中点(末尾有\0不算) 11 12 top=0;//栈的初始化 13 //将mid前的字符依次入栈 14 for(i=0;i<=mid;i++) 15 s[++top]=a[i]; 16 17 //判断字符串的长度是奇数还是偶数,并找出需要进行字符匹配的起始下标 18 if(len%2==0) 19 next=mid+1; //拿笔算算能得到 20 else 21 next=mid+2; 22 23 //开始匹配 24 for(i=next;i<=len-1;i++) 25 { 26 if(a[i]!=s[top]) 27 break; 28 top--; 29 } 30 31 //如果top的值为0,则说明栈内所有的字符都被一一匹配了 32 if(top==0) 33 printf("YES"); 34 else 35 printf("NO"); 36 return 0; 37 }
输入示例
aba
输出示例
YES
实例:纸牌游戏(队列+栈综合应用)
例题:星期天小哼和小哈约在一起玩桌游,他们正在玩一个非常古怪的扑克游戏——“小猫钓 鱼”。游戏的规则是这样的:将一副扑克牌平均分成两份,每人拿一份。小哼先拿出手中的 第一张扑克牌放在桌上,然后小哈也拿出手中的第一张扑克牌,并放在小哼刚打出的扑克牌 的上面,就像这样两人交替出牌。出牌时,如果某人打出的牌与桌上某张牌的牌面相同,即可将两张相同的牌及其中间所夹的牌全部取走,并依次放到自己手中牌的末尾。当任意一人 手中的牌全部出完时,游戏结束,对手获胜。
分析:小哼有两种操作,分别是出牌和赢牌。这恰好对应队列的两个操作,出牌就是出队,赢牌就是入队。小哈的操作和小哼是一样的。
而桌子就是一个栈,每打出一张牌放到桌上就相当于入栈。当有人赢牌的时候,依次将牌从桌上 拿走,这就相当于出栈。
那如何解决赢牌的问题呢?赢牌的规则是:如果某人打出的牌与桌上的某张牌相同,即可将两张牌以及中间所夹的牌全部取走。那如何知道桌上已经有哪些牌了呢?最简单的方法就是枚举桌上的每一张牌,当然也有更好的办法,如果打出一张2,则对book[2]进行标记,等到再打出另一张2的时候,发现标记存在,执行赢牌操作。小结一下,我们需要两个队列、一个栈来模拟整个游戏。
1 #include <stdio.h> 2 struct queue 3 { 4 int data[1000]; 5 int head; 6 int tail; 7 }; 8 struct stack 9 { 10 int data[10]; 11 int top; 12 }; 13 int main() 14 { 15 struct queue q1,q2; 16 struct stack s; 17 int book[10]; 18 int i,t; 19 20 //初始化队列 21 q1.head=1; q1.tail=1; 22 q2.head=1; q2.tail=1; 23 //初始化栈 24 s.top=0; 25 //初始化用来标记的数组,用来标记哪些牌已经在桌上 26 for(i=1;i<=9;i++) 27 book[i]=0; 28 29 //依次向队列插入6个数 30 //小哼手上的6张牌 31 for(i=1;i<=6;i++) 32 { 33 scanf("%d",&q1.data[q1.tail]); 34 q1.tail++; 35 } 36 //小哈手上的6张牌 37 for(i=1;i<=6;i++) 38 { 39 scanf("%d",&q2.data[q2.tail]); 40 q2.tail++; 41 } 42 43 while(q1.head<q1.tail && q2.head<q2.tail ) //当队列不为空的时候执行循环 44 { 45 t=q1.data[q1.head];//小哼出一张牌 46 //判断小哼当前打出的牌是否能赢牌 47 if(book[t]==0) //表明桌上没有牌面为t的牌 48 { 49 //小哼此轮没有赢牌 50 q1.head++; //小哼已经打出一张牌,所以要把打出的牌出队 51 s.top++; 52 s.data[s.top]=t; //再把打出的牌放到桌上,即入栈 53 book[t]=1; //标记桌上现在已经有牌面为t的牌 54 } 55 else 56 { 57 //小哼此轮可以赢牌 58 q1.head++;//小哼已经打出一张牌,所以要把打出的牌出队 59 q1.data[q1.tail]=t;//紧接着把打出的牌放到手中牌的末尾 60 q1.tail++; 61 62 while(s.data[s.top]!=t) //把桌上可以赢得的牌依次放到手中牌的末尾 63 { 64 book[s.data[s.top]]=0;//取消标记 65 q1.data[q1.tail]=s.data[s.top];//依次放入队尾 66 q1.tail++; 67 s.top--; //栈中少了一张牌,所以栈顶要减1 68 } 69 } 70 71 t=q2.data[q2.head]; //小哈出一张牌 72 //判断小哈当前打出的牌是否能赢牌 73 if(book[t]==0) //表明桌上没有牌面为t的牌 74 { 75 //小哈此轮没有赢牌 76 q2.head++; //小哈已经打出一张牌,所以要把打出的牌出队 77 s.top++; 78 s.data[s.top]=t; //再把打出的牌放到桌上,即入栈 79 book[t]=1; //标记桌上现在已经有牌面为t的牌 80 } 81 else 82 { 83 //小哈此轮可以赢牌 84 q2.head++;//小哈已经打出一张牌,所以要把打出的牌出队 85 q2.data[q2.tail]=t;//紧接着把打出的牌放到手中牌的末尾 86 q2.tail++; 87 while(s.data[s.top]!=t) //把桌上可以赢得的牌依次放到手中牌的末尾 88 { 89 book[s.data[s.top]]=0;//取消标记 90 q2.data[q2.tail]=s.data[s.top];//依次放入队尾 91 q2.tail++; 92 s.top--; 93 } 94 } 95 } 96 97 if(q2.head==q2.tail) 98 { 99 printf("小哼win\n"); 100 printf("小哼当前手中的牌是"); 101 for(i=q1.head;i<=q1.tail-1;i++) 102 printf(" %d",q1.data[i]); 103 if(s.top>0) //如果桌上有牌则依次输出桌上的牌 104 { 105 printf("\n桌上的牌是"); 106 for(i=1;i<=s.top;i++) 107 printf(" %d",s.data[i]); 108 } 109 else 110 printf("\n桌上已经没有牌了"); 111 } 112 else 113 { 114 printf("小哈win\n"); 115 printf("小哈当前手中的牌是"); 116 for(i=q2.head;i<=q2.tail-1;i++) 117 printf(" %d",q2.data[i]); 118 if(s.top>0) //如果桌上有牌则依次输出桌上的牌 119 { 120 printf("\n桌上的牌是"); 121 for(i=1;i<=s.top;i++) 122 printf(" %d",s.data[i]); 123 } 124 else 125 printf("\n桌上已经没有牌了"); 126 } 127 128
129 return 0; 130 }
链表(指针版)
概念
struct node { int data; struct node *next; };
定义一个叫做 node 的结构体类型,这个结构体类型有两个成员。 第一个成员是整型 data,用来存储具体的数值;第二个成员是一个指针,用来存储下一个结点的地址。因为下一个结点的类型也是 struct node,所以这个指针的类型也必须是 struct node * 类型的指针。
实例:插入数字
任务:创建一个链表,写入n个节点,新增一个节点,按升序排序,并输出链表所有节点。
1 #include <stdio.h> 2 #include <stdlib.h> 3 //这里创建一个结构体用来表示链表的结点类型 4 struct node 5 { 6 int data; 7 struct node *next; 8 }; 9 int main() 10 { 11 struct node *head,*p,*q,*t; 12 int i,n,a; 13 scanf("%d",&n); 14 head = NULL;//头指针初始为空 15 for(i=1;i<=n;i++)//循环读入n个数 16 { 17 scanf("%d",&a); 18 //动态申请一个空间,用来存放一个结点,并用临时指针p指向这个结点 19 p=(struct node *)malloc(sizeof(struct node)); 20 p->data=a;//将数据存储到当前结点的data域中 21 p->next=NULL;//设置当前结点的后继指针指向空,也就是当前结点的下一个结点为空 22 if(head==NULL) 23 head=p;//如果这是第一个创建的结点,则将头指针指向这个结点 24 else 25 q->next=p;//如果不是第一个创建的结点,则将上一个结点的后继指针指向当前结点 26 q=p;//指针q也指向当前结点 27 } 28 29 /*以上过程很妙,需要在纸上画出来理解 30 以下为插入新节点(按升序)的过程 */ 31 32 scanf("%d",&a);//读入待插入的数 33 t=head;//从链表头部开始遍历 34 while(t!=NULL)//当没有到达链表尾部的时候循环 35 { 36 if(t->next->data > a)//如果当前结点下一个结点的值大于待插入数,将数插入到中间 37 { 38 p=(struct node *)malloc(sizeof(struct node));//动态申请一个空间,用来存放新增结点 39 p->data=a; //写入新节点的值 40 p->next=t->next;//新增结点的后继指针 指向 当前结点的后继指针 所指向的结点 41 t->next=p;//当前结点的后继指针指向新增结点 42 break;//插入完毕退出循环 43 } 44 t=t->next;//继续遍历下一个结点 45 } 46 47 /*以上过程为插入新节点的过程 48 以下为输出链表中的所有数的过程 */ 49 50 t=head; 51 while(t!=NULL) 52 { 53 printf("%d ",t->data); 54 t=t->next;//继续下一个结点 55 } 56 57 return 0; 58 }
模拟链表(双数组模拟)
概念
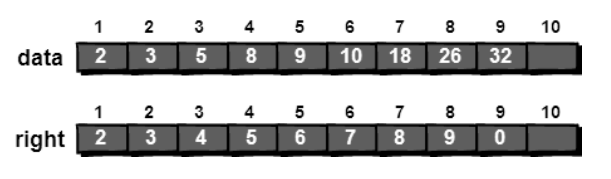
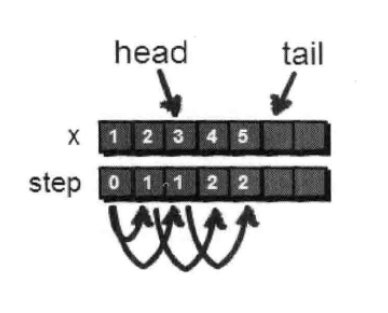
用一个数组 data 来存储序列中的每一个数,再用一个数组right来存放序列中每一个数右边的数是谁。(right数组最后一位初始化为0,模拟指向NULL)
right[1]的值为2,表示序列中1号元素右边的元素存放于data[2]中,即data[right[1]]=data[2]
如果要在data[3]与data[4]之间插入一个数字6:
1.只需要令data[10]=6,right[3]=10,表示新序列中3号元素右边的元素存放在data[10]中。
2.再将right[10] 改为 4,表示新序列中 10 号元素右边的元素存放在 data[4]中。
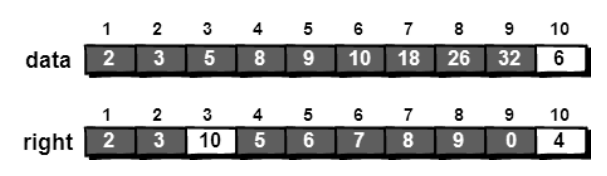
代码实现
#include<stdio.h> int main() { int data[101]; int right[101]; int i, n, len, t; printf("请输入节点数:"); scanf("%d", &n); printf("请输入%d个数:", n); for (i=1; i<=n; i++) { scanf("%d", &data[i]);//读入已有数据 } len = n; for (i=1; i<=n; i++)//初始化数组right { if (i != n) { right[i] = i + 1; } else { right[i] = 0; } } printf("请输入待插入数据:"); len++; scanf("%d", &data[len]);//将所插入数加在数组data末尾 t = 1;//从链表头部开始遍历 while (t !=0) { if (data[right[t]] > data[len])//如果当前结点下一个结点的值大于待插入数据,将数插入到中间 { right[len] = right[t];//新插入数的下一个结点标号等于当前结点的下一个结点编号 right[t] = len;//当前结点的下一个结点编号就是新插入数的编号 break; //插入完跳出循环 } t = right[t]; } t = 1;//输出链表所有数 printf("插入数据后:"); while (t != 0) { printf("%d ", data[t]); t = right[t]; } return 0; }
第三章:枚举
实例:简单穷举
问题:

分析:
循环九个变量,将所有循环过的变量标记至book数组,如果book数组计数器为9,即出现了9个不同的数,进行等式验证,如成立则输出。
代码实现:
P.S:太暴力了,运行时间特长!
1 #include <stdio.h> 2 int main(void) 3 { 4 int a[10],book[10]; 5 int sum = 0; 6 int cnt = 0; 7 for(a[1] = 1; a[1] <= 9; a[1]++) 8 for(a[2] = 1; a[2] <= 9; a[2]++) 9 for(a[3] = 1; a[3] <= 9; a[3]++) 10 for(a[4] = 1; a[4] <= 9; a[4]++) 11 for(a[5] = 1; a[5] <= 9; a[5]++) 12 for(a[6] = 1; a[6] <= 9; a[6]++) 13 for(a[7] = 1; a[7] <= 9; a[7]++) 14 for(a[8] = 1; a[8] <= 9; a[8]++) 15 for(a[9] = 1; a[9] <= 9; a[9]++){ 16 for(int i = 1; i <= 9; i++) 17 book[i] = 0; 18 for(int i = 1; i <= 9; i++){ 19 book[a[i]] = 1; 20 if(book[a[i]] == 1) 21 sum++; 22 } 23 if(sum == 9 && a[1]*100 + a[2]*10 + a[3] + a[4]*100 + a[5]*10 24 + a[6] == a[7]*100 + a[8]*10 + a[9]) 25 cnt++; 26 } 27 printf("%d",cnt/2); 28 return 0; 29 }
实例:炸弹人
穷举每一个点,选出最大值。
现存问题:无法计算路径,有些情况下路径无法到达。




实例:火柴棍
问题:


分析:首先分析A,B,C的穷举范围,m取最大值,删去加号和等于号占去的4根火柴,剩余20根火柴。注意到构成一个数字所需的最少火柴数为2(数字1),且构成数字时:位数对大小的作用大于每一位的值,所以为了得出最大的数字,考虑使用剩余20根火柴拼出10个数字1,问题转化为用10个数字1来拼凑[ ] + [ ] = [ ]这样一个等式,使用8个1,显然无法构成等式,使用7个1,显然无法构成等式......直到使用4个1,考虑剩余十二根火柴有可能能构成等式。为减少算法的时间复杂度,先枚举A,B,在通过A+B=C计算出C。
代码实现:
1 #include <stdio.h> 2 int ret(int a); 3 int main(void) 4 { 5 int m,i,j; 6 m = 18; 7 for (i = 0;i < 1111;i++) 8 for(j = 0;j < 1111;j++){ //穷举A,B 9 int k = i + j; 10 11 if(ret(i) + ret(j) + ret(k) + 4 == m){ //判断火柴棒数是否合理 12 printf("%d + %d = %d\n",i,j,k); 13 } 14 } 15 return 0; 16 17 } 18 int ret(int a){ 19 int A[] = {6, 2, 5, 5, 4, 5, 6, 3, 7, 6}; //各个位数字所需火柴棒 20 int sum = 0; 21 int t; 22 while(a / 10 > 0){ //当a为十位数时提取每一位所需的火柴棒 23 sum += A[a%10]; 24 a/=10; 25 } 26 sum += A[a]; //加上最前一位的火柴棒 27 return sum; 28 }
实例:全排列
介绍了嵌套多层循环的全排列,如要计算123...n的全排列,详见下一章搜索。
第四章:搜索
深度优先搜索(DFS)
引入:放扑克牌
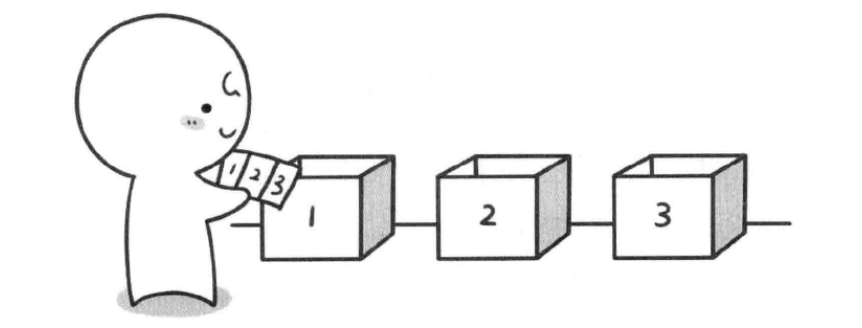
问题:1,2,3三个盒子,依次放扑克牌,求放扑克牌的全排列?
解:约定在每个盒子面前以1,2,3的顺序放扑克牌,当走到第4个盒子(虚构)时,返回到三号盒子,此时拿回3号牌,回到2号盒子,拿回2号牌,按顺序放置三号牌,前往三号盒子,放置手中仅有的二号牌。按照以上步骤,生成所有排列。
代码实现:
DFS关键在于解决“当下该如何做”,至于”下一步如何做“与”当下该如何做“是一样的。
基本模型:

1 #include <stdio.h> 2 void dfs(int step); 3 int a[10],book[10],n; 4 int main(){ 5 scanf("%d",&n); //n代表求1-n的全排列 6 dfs(1); //从第一步开始 7 return 0; 8 } 9 void dfs(int step){ 10 int i; 11 //边界条件:在第n+1个盒子面前 12 if(step > n){ 13 for(i = 1; i <= n; i++){ //输出所有盒子内数字 14 printf("%d",a[i]); 15 } 16 printf("\n"); 17 } 18 //站在第step个盒子面前 19 for(i = 1; i <= n; i++){ 20 if(book[i] != 1){ //牌i还在手里面 21 book[i] = 1; //出牌 i 22 a[step] = i; //第step个箱子里放入牌i 23 dfs(step + 1); //下一步 24 book[i] = 0; //收牌 i 25 } 26 } 27 }
实例:解救小哈
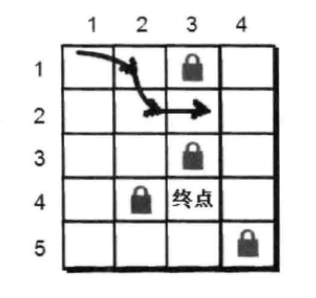
问题:从(1,1)到(4,3),要求找出最短路径。
分析:采用DFS,边界条件为是否已经到终点,如果满足边界条件,则更新最小值。在第(i,j)格枚举四种走法,判断是否越界以及障碍物,若满足,则标记该点并尝试以该点下一个点,递归返回时取消该点标记。
代码实现:略,见书P86。
广度优先搜索(BFS)
例1:走迷宫
分析:(1,1)为初始点,先对其进行拓展,通过判断越界及障碍物条件分别拓展四个方向,拓展出(1,2)及(2,1)两个新节点。再对(1,2)进行拓展,拓展出(2,2)节点......以此类推,直到抵达目标点,记录步数。
代码实现:见 P92
例2:炸弹人

分析:之前的炸弹人算法无法判断小人可抵达的点,现用搜索算法升级。用广度优先搜索或深度优先搜索遍历所有可抵达点,对每一个可抵达点,计算在该点可消灭敌人数并更新最大值(上一章)
代码实现:见 P98,P102
实例:小岛探险
Floodfill漫水填充法
作用:求一个图中独立子图的个数
仅需在dfs函数中新加一个参数color即可

第五章:图的遍历
如何遍历一个图?
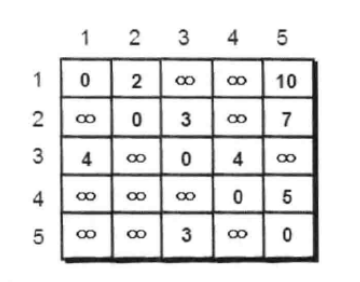
图的概念及邻接矩阵表示法
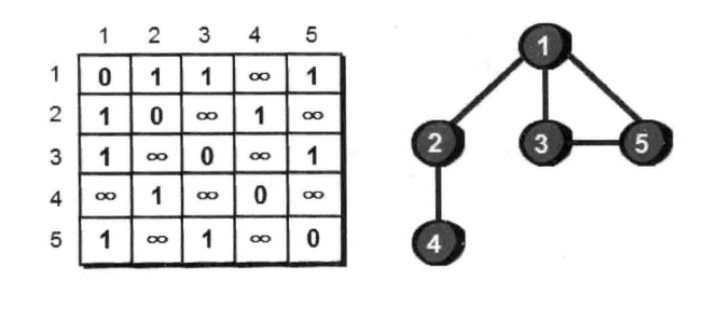
该图为无向图,邻接矩阵沿中心线对称。(1,1)表示该节点离自身距离为0,(1,4)表示无法到达,常用一个大数字替代无穷大,(1,2)表示节点1到节点2距离为1.
代码实现:(DFS)
1 #include <stdio.h> 2 int e[101][101]; 3 int book[101]; 4 void dfs(int node,int n); 5 int main() 6 { 7 int a,b,n,m; 8 scanf("%d %d",&n,&m); 9 for(int i = 1; i <= n; i++) //初始化邻接矩阵 10 for(int j = 1; j <= n; j++){ 11 if(i == j) 12 e[i][j] = 0; 13 else 14 e[i][j] = 9999; 15 } 16 17 for(int i = 1; i <= n; i++){ //初始化邻接矩阵 18 scanf("%d %d",&a,&b); 19 e[a][b] = 1; 20 e[b][a] = 1; 21 } 22 book[1] = 1; 23 dfs(1,n); 24 return 0; 25 } 26 void dfs(int node,int n){ 27 int sum; 28 sum++; 29 printf("%d ",node); 30 if(sum == n){ 31 return; 32 } 33 for(int i = 1; i <= n; i++){ 34 if(e[node][i] == 1 && book[i] == 0){ 35 book[i] = 1; 36 dfs(i,5); //这里不需要设置book[i]为0,排列问题取消是为了新的排列 37 } 38 } 39 return; //拓展完该节点后返回 40 }
代码实现:(BFS)
1 #include <stdio.h> 2 int e[101][101]; 3 int book[101]; 4 int q[101]; 5 void bfs(int node,int n); 6 int main() 7 { 8 int a,b,n,m; 9 scanf("%d %d",&n,&m); 10 for(int i = 1; i <= n; i++) //初始化邻接矩阵 11 for(int j = 1; j <= n; j++){ 12 if(i == j) 13 e[i][j] = 0; 14 else 15 e[i][j] = 9999; 16 } 17 18 for(int i = 1; i <= n; i++){ //初始化邻接矩阵 19 scanf("%d %d",&a,&b); 20 e[a][b] = 1; 21 e[b][a] = 1; 22 } 23 book[1] = 1; 24 bfs(1,n); 25 return 0; 26 } 27 void bfs(int node,int n){ 28 int head = 1; 29 int tail = 1; 30 q[1] = 1; 31 tail++; //初始化队列,设置1号位为1 32 while(tail > head){ //当队列不为空时 33 node = q[head]; //更新当前拓展节点 34 for(int i = 1; i <= n; i++){ 35 if(book[i] == 0 && e[node][i] == 1){ 36 q[tail] = i; 37 tail++; 38 book[i] = 1; //入队,设置已访问 39 } 40 if(tail > n){ //边界条件 41 break; 42 } 43 } 44 head++; //更新当前拓展节点 45 } 46 for(int j = 1; j <= n; j++){ //输出队列 47 printf("%d ",q[j]); 48 } 49 }
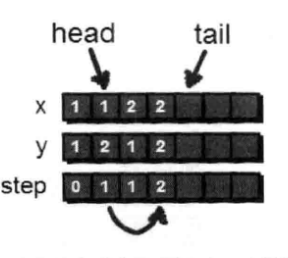
BFS较为适用于距离为1的情况。
实例:走地图
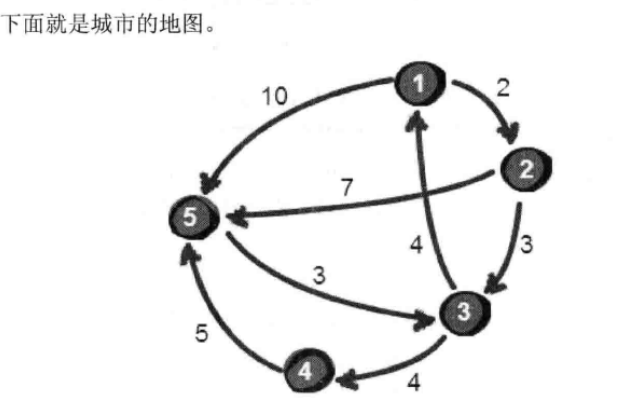
有向图,且距离权重不一致,采用深度优先搜索。
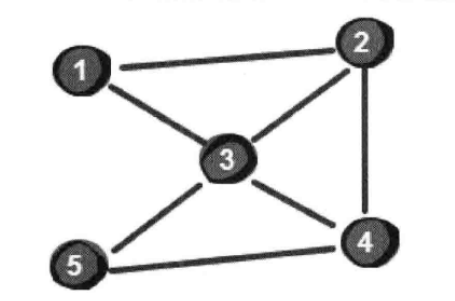
实例:航班的最少次数
无向图,权重相等,采用广度优先搜索。
第六章:最短路径
Floyd-Warshall算法(多源最短路径) -FW算法
问题:
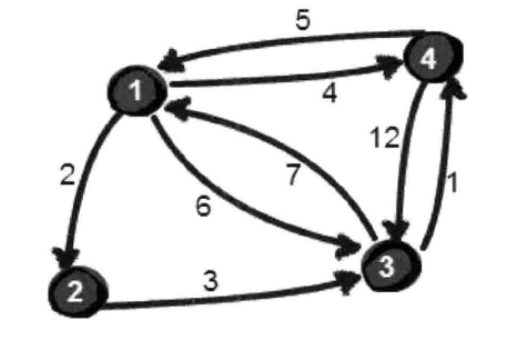
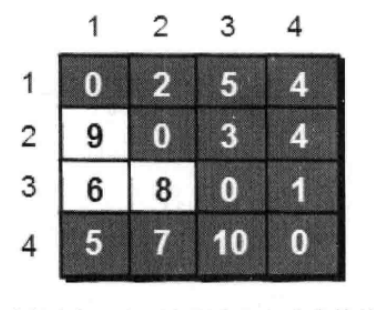
上图中有4个城市8条公路,公路上的数字表示这条公路的长短。请注意这些公路是单向的。我们现在需要求任意两个城市之间的最短路程,也就是求任意两个点之间的最短路径。这个问题这也被称为“多源最短路径”问题。
算法及其分析:
1.建立邻接矩阵存储各节点之间距离。
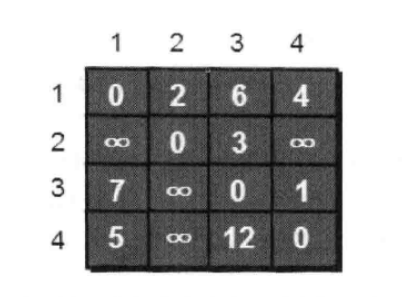
2.只允许经过1号顶点,比较 e[ i ][1] + e[1][ j ] 和 e[ i ][ j ] 大小关系,更新任意两点间的最短路径。
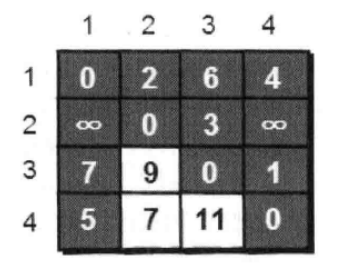
3.允许经过2号顶点,重复上述操作...直到允许经过4号顶点,重复以上过程后,得到更新后的邻接矩阵。
代码实现:
最外层循环n次,内两层循环遍历每个顶点距离,对每个顶点距离判断经过各顶点后距离是否缩短。

Dijkstra算法(通过边实现松弛) -DJ算法
问题:
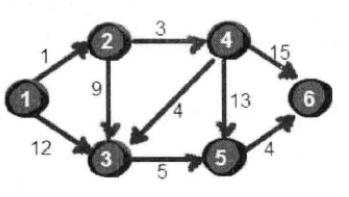
指定一个点(源点)到其余各个顶点的最短路径,也叫做“单源最短路径”。例如求下图中的1号顶点到2、3、4、5、6号顶点的最短路径。
算法及其分析:
1.将所有的顶点分为两部分:已知最短路程的顶点集合P和未知最短路径的顶点集合Q。最开始,已知最短路径的顶点集合P中只有源点一个顶点。
用一个book[ i ]数组来记录哪些点在集合P中。例如对于某个顶点i,如果book[ i ]为1则表示这个顶点在集合P中,如果book[ i ]为0则表示这个顶点在集合Q中。
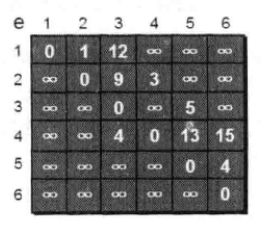
2.设置源点s到自己的最短路径为0即dis=0。若存在源点有能直接到达的顶点i,则把dis[ i ]设为e[ s ][ i ]。同时把所有其它(源点不能直接到达的)顶点的最短路径为设为∞。

3.在集合Q的所有顶点中选择一个离源点s最近的顶点u(即dis[u]最小)加入到集合P。并考察所有以点u为起点的边,对每一条边进行松弛操作。
松弛:例如存在一条从u到v的边,那么可以通过将边u->v添加到尾部来拓展一条从s到v的路径,这条路径的长度是dis[u]+e[u][v]。如果这个值比目前已知的dis[v]的值要小,我们可以用新值来替代当前dis[v]中的值。
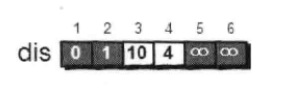

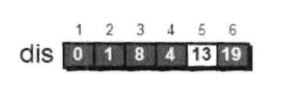

4.重复第3步,如果集合Q为空,算法结束。最终dis数组中的值就是源点到所有顶点的最短路径。
代码实现:
1 #include <stdio.h> 2 int main() 3 { 4 int e[10][10],dis[10],book[10],i,j,n,m,t1,t2,t3,u,v,min; 5 int inf=99999999; //用inf(infinity的缩写)存储一个我们认为的正无穷值 6 //读入n和m,n表示顶点个数,m表示边的条数 7 scanf("%d %d",&n,&m); 8 9 //初始化 10 for(i=1;i<=n;i++) 11 for(j=1;j<=n;j++) 12 if(i==j) e[i][j]=0; 13 else e[i][j]=inf; 14 15 //读入边 16 for(i=1;i<=m;i++) 17 { 18 scanf("%d %d %d",&t1,&t2,&t3); 19 e[t1][t2]=t3; 20 } 21 //初始化dis数组,这里是1号顶点到其余各个顶点的初始路程 22 for(i=1;i<=n;i++) 23 dis[i]=e[1][i]; 24 //book数组初始化 25 for(i=1;i<=n;i++) 26 book[i]=0; 27 book[1]=1; 28 29 //Dijkstra算法核心语句 30 for(i=1;i<=n-1;i++) //重复n-1次该过程,直到把所有点距离变为确定值 31 { 32 //找到离1号顶点最近的顶点 33 min=inf; 34 for(j=1;j<=n;j++) 35 { 36 if(book[j]==0 && dis[j]<min) 37 { 38 min=dis[j]; 39 u=j; 40 } 41 } 42 book[u]=1; //作出标记,加入确定值 43 for(v=1;v<=n;v++) //更新最小值 44 { 45 if(e[u][v]<inf) 46 { 47 if(dis[v]>dis[u]+e[u][v]) 48 dis[v]=dis[u]+e[u][v]; 49 } 50 } 51 } 52 53 //输出最终的结果 54 for(i=1;i<=n;i++) 55 printf("%d ",dis[i]); 56 57 getchar(); 58 getchar(); 59 return 0; 60 }
Bellman-Ford算法(解决负权边) - BF算法
问题:
DJ算法无法解决带有负权重边的单源最短路径问题,考虑采用BF算法。
代码实现:

另:书中还提到了检测负权回路及降低时间复杂度的改进,详见P170。
BF算法队列优化
没看明白,以后再来填坑!
问题:
算法及其分析:
代码实现:
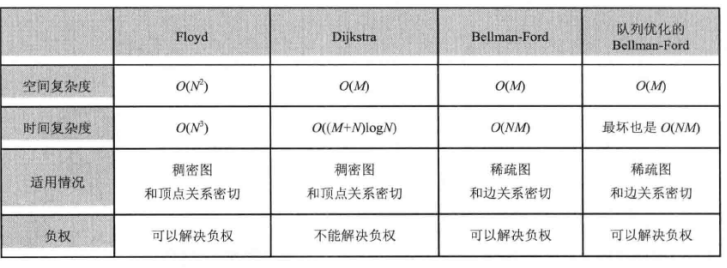
小结


 浙公网安备 33010602011771号
浙公网安备 33010602011771号