【黑金原创教程】【TimeQuest】【第一章】TimeQuest 静态时序分析模型的概念
声明:本文为黑金动力社区(http://www.heijin.org)原创教程,如需转载请注明出处,谢谢!
黑金动力社区2013年原创教程连载计划:
http://www.cnblogs.com/alinx/p/3362790.html
《FPGA那些事儿--TimeQuest 静态时序分析》REV1.0 PDF下载地址:
http://www.heijin.org/forum.php?mod=viewthread&tid=22309&extra=page%3D1
第一章:TimeQuest 静态时序分析模型的概念
1.1模型的基础单位
1.2理想的建立关系值和保持关系值
1.3 物理中的建立关系过程和建立余量
1.4 令人误会的建立关系 和 建立余量
1.5 建立余量
1.6 保持余量
第一章:TimeQuest 静态时序分析模型
兜兜转转,然后又转转兜兜,最终还是需要站在 TimeQuest 的大门口。先自白一下,接下来的故事都是一位傻子对TimeQuest的理解,这个傻子的脑容量有限,处理能力不好,空白的地方都会用想象力自园。
TimeQuest 是 Altera - Quartus II 旗下的东西,其中它(TimeQuest)用了一个“时序分析模型”作为物理时序的分析“框子”或者“数学模型”。在这里笔者需要强调一下,TimeQuest中的“时序”和Verilog HDL中出现的时序是两个东西。所谓HDL的时序是指“模块的活动记录”等理想的波形;反之 TimeQuest 中出现的时序是指“物理上路径,各种延迟问题”的不理想波形。
让我们暂时把Verilog HDL忘了吧 ... 一般上分析物理时序有用一套方法称为“静态时序分析”的方法,关于静态时序分析网上有太多的解释了,但是TimeQuest 有属于自己一套“分析时序的模型”,所以我们可以“无视”其它。
1.1模型的基础单位
图1.1.1 模型的基础
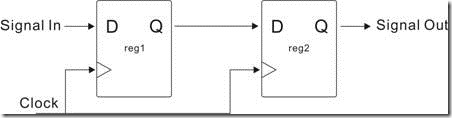
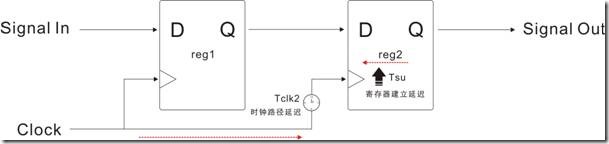
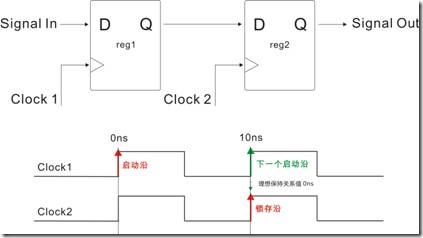
TimeQuest的时序分析模型(以下简称模型)的基础,基本上需要两个节点才能发挥,如图1.1.1所示。节点的定义很模糊,因为节点本身没有个性,它处在什么就变什么 ... 如果用TimeQuest的话来讲,将一对节点放在fpga内部,节点就会化身成为寄存器。这也节点最常见的姿态。所以说,暂时让我们把节点看成寄存器吧!
图1.1.2 寄存器为节点
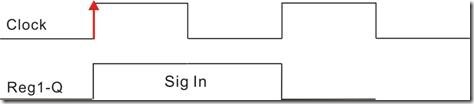
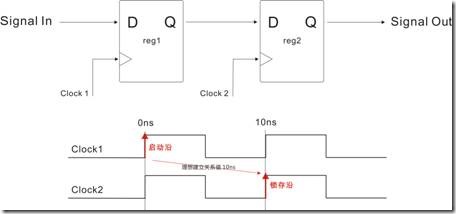
图1.1.2是把另个节点看成寄存器,亦即寄存器1(reg1)和寄存器2(reg2)。寄存器1和寄存器2共享同样的时钟信号。Signal(信号)从寄存器1的D进入,再由寄存器1的Q游走,然后从寄存器2的D进入,最后再经寄存器2的Q出走。上述的寄存器活动,按“理想时序”会产生图1.1.3的时序图。
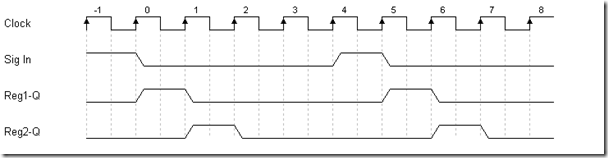
图1.1.3 理想时序
如图1.1.3所示 ... 所谓理想——就是“不存在任何物理上的延迟”,T-1之际是初始化状态,Sig In的初值为1,然后在T0的时候寄存器1读取Sig In的过去值,亦即逻辑1。在T0的未来寄存器1输出逻辑1长达一个时钟周期。在T1的时候,寄存器2读取Reg1-Q的过去值,亦即逻辑1,然后在T1的未来寄存器2拉高输出长达一个时钟周期。
根据“模块沟通”而言,每一个寄存器至少需要消耗1个时钟,在此 Sig In 经过两个寄存器,也就是它延迟了2两个时钟,从最开始到最后的Reg2-Q输出。
“理想时序和TimeQuest模型到底有什么关系?”——笔者一直在苦恼这个问题。要完全理解TimeQuest的模型,理想时序作的角色有“参考”和“比较”的作用。在前面笔者说过了,TimeQuest的模型需要一对节点才能成立,这是铁一般的基础,但是Time Quest模型它才不在乎时序的整个过程,而它只在乎“Reg1发送数据给Reg2然后Reg2读取数据这一段时间”而已。
TimeQuest模型中有两个关键关系,亦即建立关系和保持关系。老实说要很好的明白它们之间的定义,还是真是不简单,笔者也耗了很长的时间去整理思想,然后才能得出零星的总结。在此,我们需要借助“理想时序”的力量,唯有如此才能更好了解TimeQuest模型。
1.2理想的建立关系值和保持关系值
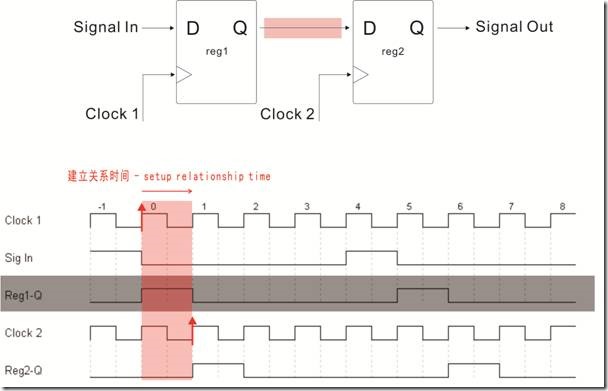
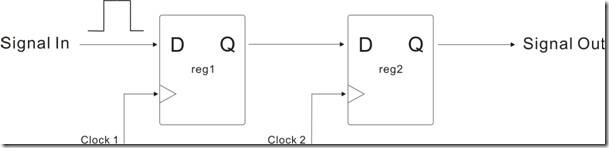
图1.2.1 理想的建立关系值
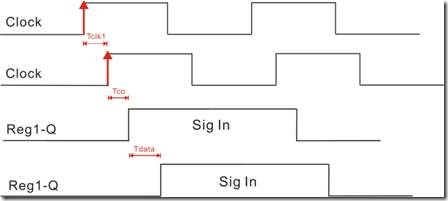
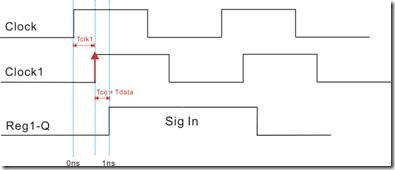
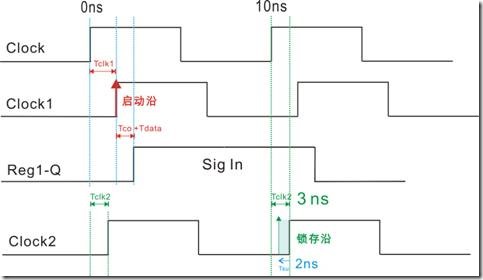
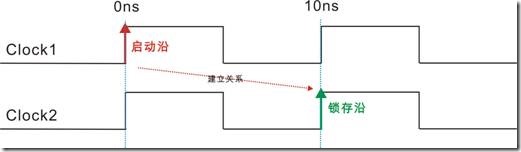
图1.2.1的一对节点,该reg1和reg2都有自己专属的时钟信号,亦即Clock1 和 Clock2。在T0的时候,reg1决定向 reg2 发送数据,同学们请注意时序图的箭头“→",该数据长达一个周期时间,这段时间也称为“建立关系值”或者“建立关系时间”。
“建立关系值”的定义是指——在T0的时候 Clock1的上升沿使得 reg1 给 reg2输出数据,这个上升沿也称为“启动沿 - lunch edge”。在T1的时候,Clock2的上升沿使得reg2 保存 reg1发过来的数据,这个Clock2的上升沿也称为“锁存沿 - latch edge”
然而该启动沿与锁存沿之间的长度就是“建立关系值|建立关系时间”。
在理想的状态下,如果 reg1 和 reg2 使用相同频率的时钟,那么:
建立关系值 = 时钟周期
假设 Clock1 和 Clock2 都是 20Mhz 频率,那么建立关系值是 50ns。
既然有建立关系值当然也有保存关系值,但是关于保存关系值的概念确实会比较头疼, 笔者抓到头秃了 ... 要理解保存关系值,基本上又要从锁存时间开明白。所谓锁存时间就是reg2 用来锁存 reg1发送过来数据所需的“最小时间”。在理想的状态下,锁存时间几乎是 0 或者 瞬间。
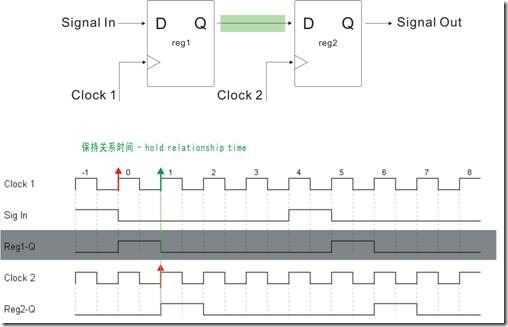
图1.2.2 保持关系值
如图1.2.1所示,在T0的时候Clock1的启动沿(红色的箭头↑)使得 reg1向 reg2发送数据。然后在T1的时候(我们先看Clock2的红色键头↑)Clock2 的锁存沿使得reg2保存reg1发送过来的数据。
保持关系的定义是指——Clock1的另一个上升沿来到之前(Clock1的绿色箭头),reg2要最快的速度将数据读取。换句话说,reg1在T0向reg2发送的数据,而reg2乘数据还没有更新之前,reg2必须迅速的将 reg1 在T0发送过来的数据保存起来。(在理想的时序下 reg2的锁存所需的时间是0)
所以说,我们可以这样决定保持关系值,亦即“Clock1的下一个启动沿 至 当前Clock2的锁存沿 之间的长度”。在理想的状态下,如果 reg1 和 reg2 使用相同的时钟频率,那么一定:
保持关系值 = 0ns
在这里,笔者需要再强调一下,在实际的物理情况下不可能会有0ns的保持关系值,然而reg2锁存数据所使用的时间也不会是 0ns。同学们需要好好的记住,理想时序仅是一种直观的表达而已。
有些朋友会纳闷道:“建立关系值和想保持关系值到底在TimeQuest 模型中扮演什么有角色?”呵呵,用处可真大了 ... 笔者根据自己的理解,它们有3大用处:
(一)对物理时序分析有直观的表达
(二)简化TimeQuest模型分析
(三)为物理时序取等价关系图
1.3 物理中的建立关系过程和建立余量
建立余量是什么?在建立关系的过程中,“正值的建立余量”代表了“两个节点之中的建立关系是合格”。让我们一步一步来理解吧:
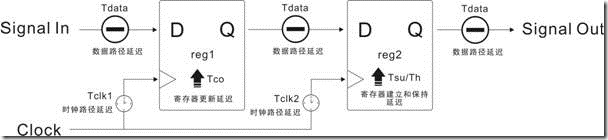
图1.3.1 物理上的延迟
图1.3.1所示,有一对节点上出现许多骇人的东西,这就是我们所谓的物理时序,而那些骇人的东西就是内部延迟因数。物理时序和理想时序就像水火不容的好兄弟,不过它们再怎么糟,身上也有同样的血亲(黏糊关系)。物理时序的产生是Verilog HDL经过综合后(FPGA布线完成后)才会产生,然而理想时序是 Verilog HDL所描述模块会出现的“活动记录”或者“沟通记录”。
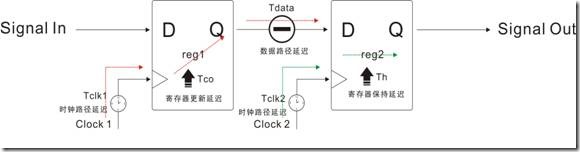
我们来看看图1.3.1 有什么样的延迟因数呢? Tclk1 和 Tclk2本是时钟路径延迟,别名 clock path;Tdata是指数据路径延迟,也称 data path;Tco是寄存器发送数据时需要的“最小持续(更新)时间”,Tsu是寄存器在锁存数据前时需要的"最小准备时间",反之 Th 是寄存器在锁存数据过后需要的“最小确保时间”,而Tco,Tsu和Th也称为寄存器特性。
在图1.3.1出现的延迟因数会大大的影响时序表现,尤其是“建立关系和保持关系”。不过,不同的延迟因数都会出现在特定的场合。换句话说,当我们分析建立余量的时候,必定会出现某个特定的延迟因素;然后,在我们分析保持余量的时候,又会某个特定的延迟因数。
好了,我们先来看看在建立关系的过程中,会出现什么延迟因数呢?
图1.3.2 延迟因素影响建立关系
在前面笔者已经说过,计算建立关系的长度(建立关系值)需要“先”考虑reg1向reg2发送数据的启动沿。理想情况reg1会无视一切延迟因数,反之物理情况reg1发送数据给reg2的时候就必须考虑 Tclk1 + Tco + Tdata 的等延迟。
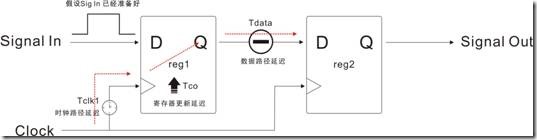
图1.3.3 被延迟因素影响 (物理状态)
图1.3.3 是reg1发送数据时受延迟因数影响的经过 ... Clock的上升沿来到reg1之前,clock 受到 Tclk1 的延迟 ... 当clock的启动沿(红色箭头)触发 reg1 reg1向 reg2 发送数据之际,reg1还要需要 Tco的热身时间(更新数据)。当经过 Tco的延迟之后,数据终于从 Reg1-Q发送出去了 ...
可以在它前面的还有 Tdata 的延迟。Tdata 延迟的产生源除了路径本身的延迟以外,最最主要还是“组合逻辑”。最后reg1向 reg2发送的数据经过 Tdata的延迟之后就抵达reg2 的入口(reg2-D)。
图1.3.4 理想状态
相反的图1.3.4是理想时序而里边不包含何延迟。当 Clock 的启动沿触发 reg1以后,reg1就会立即输出数据。而已,还有锁存沿这一方。如果用了一条公式评估 Tclk1 + Tco + Tdata 对启动沿的影响:
数据抵达时间 Data Arrival Time = 启动沿时间 + Tclk1延迟 + Tco延迟 + Tdata延迟
这公式的定义很简单:
“在分析建立关系的过程中,假设reg1 向 reg2在某个启动沿T发送数据,当经过 Tclk1 + Tco + Tdata 等延迟因素,而该启动沿 T 会产生多少位移呢?”
图1.3.5 例子
举个例子,假设reg1 在0ns的时候向 reg2 发送数据,而Tclk1 + Tco + Tdata 等总和延迟时间是 1ns,那么启动沿会被位移至 1ns,如图1.3.5所示。在前面笔者说过,如果要分析建立关系值,单是评估延迟因数对启动沿的影响是不足的,因为造就建立关系,除了启动沿以外,还有锁存方(reg2)的锁存沿。
图1.3.6 锁存沿受延迟因数的影响
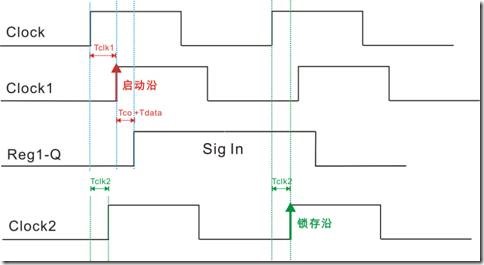
要明白锁存方如何造就建立关系的结果(建立关系值),我们考虑考虑锁存方的寄存器特性还有锁存方的时钟路径,如图1.3.6所示的Tclk2 和 Tsu。Tclk2 是锁存沿抵达 reg2 之前,时钟路径的延迟。反之 Tsu 是在 reg2 要锁存从reg1发来的数据之前,需要的最小准备时间。
图1.3.7
图1.3.7是建立关系考虑锁存方的物理时序。Clock是源时钟,又或者理想时钟,而Clock1 是经过 Tclk1 延迟以后,reg1的时钟源(注意那个启动沿);Clock2 是经过 Tclk2 延迟以后,reg2的时钟源(注意那个锁存沿),而Tclk2延迟造成了 reg2时钟源的位移。 clock2 经过Tclk2 延迟之后 reg2 终于迎来了自己的锁存沿 ... 接下我们要注意的家伙是Tsu,亦即锁存方的寄存性特性。
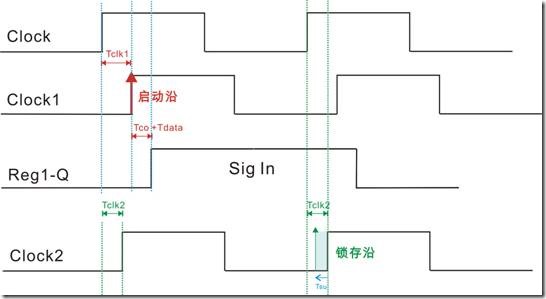
图1.3.8 Tsu延迟因素的影响
Tsu 的定义是指“寄存器2在锁存之前需要的最小准备时间”。如图1.3.6所示,Tsu的箭头方向与 Tclk2 的箭头方向是相冲的,这也使得 Tsu 将锁存沿左移,随之造就 图1.3.8的相冲结果。同样TimeQuest模型也用了一条公式来评估 锁存沿受 Tclk2 和 Tsu 的影响:
数据锁存(读取|保存)时间 Data Required Time = 锁存沿时间 + Tclk2 - Tsu
这一条公式的定义很简单:
“在分析建立关系的过程中,锁存时间就是reg2欲读取数据之际,而锁存沿受Tclk2影响影响以后会右移几点,接着Tsu再将锁存沿左移几点”
假设一个例子:
图1.3.9 例子
如图1.1.9所示,在理想的状态下 ... 锁存沿的时间原本是 10ns,但是经Tclk2的延迟向右位移几点,成为 10ns + 3ns = 13ns。然后锁存沿又受到 Tsu 影响所以又向左移几点,成为 13ns - 2ns = 11ns,最终reg2的锁存时间是 11ns。
1.4 令人误会的 建立关系 和 建立余量。
还没有进入建立余量这个主题之前笔者有责任,简单的刷新刷新一下那些封尘已久的记忆还有一误点。建立关系被TimeQuest称为 "Setup Relationship", 事实上这个“Setup Relationship”是评估(计算)建立余量(setup lack)的一个过程。但是,不知曾经何时,在很多文章中 Setup Relationship 的定义忽然模糊起来...
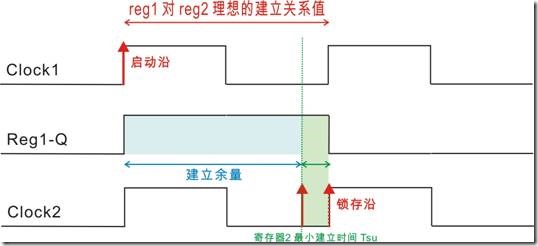
图1.4.1 理想建立关系值
如图1.4.1所示,在理想的状态下“建立关系值”是10ns ... 那么问题来了,在这里我们需要严重的注意这个“10ns”,而这个“10ns”是一个建立关系值,而Setup Relationship 是指“分析建立关系的过程”... 结果很明显 :
1. 这个“10ns” ≠ Setup Relationship。
2. 这个“10ns”是一个理想值而已。
3. 这个“10ns”理想值,在 Setup Relaionship 过程是“建立余量”的最好结果!
虽说,上述的内容仅是笔者的想法而已,但是笔者始终认为,建立关系只是一个过程,建立关系值是一个有用的理想值,而这个理想值是建立余量最理想的结果。
1.5 建立余量
建立余量英文是 setup slack,它是 TimeQuest 模型中重要的结果之一,正值的建立余量使得两个寄存器有合格的建立关系。建立余量实际上一点也不难理解,让笔者慢慢解释吧:
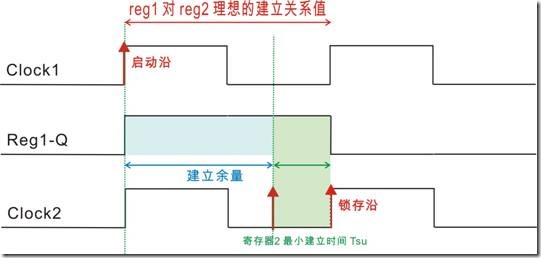
图1.5.1理想时序图
图1.5.1有一对节点和和理想的建立关系过程,寄存器1和寄存器2各自都是用相同的源时钟,无论 Clock1 还是 Clock2 的时钟周期都是10ns。在图1.5.1中,Clock1 和 Clock2 之前的建立关系值是10ns。
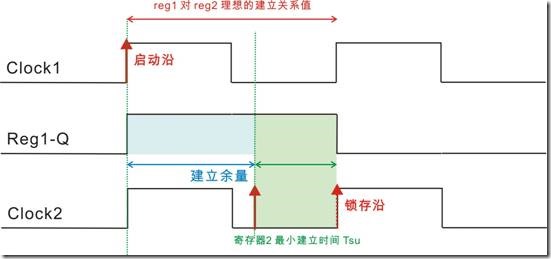
图1.5.2 物理的时序图
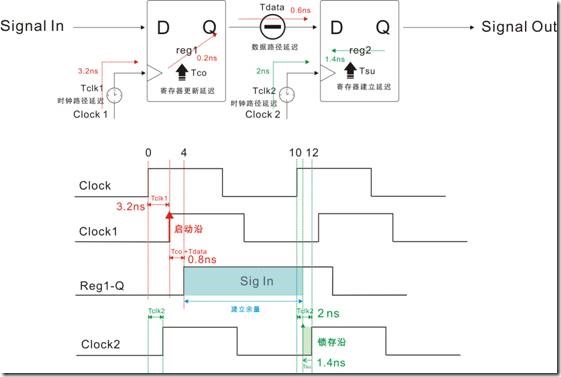
图1.5.2 是物理的建立关系过程,寄存器1和寄存器2也使用拥有相同属性的时钟源。而图1.5.2和图1.5.1之间的区别是,图1.5.2有一大堆的延迟。我们接下来的工作就是要取得建立余量。
首先要取得 Clock1 的启动沿受延迟的影响,而TimeQuest模型用了一条公式评估启动沿受 Tclk1 + Tco + Tdata 的影响:
数据抵达时间 Time Arrival Time = 启动沿时间 + Tclk1 + Tco + Tdata
= 0ns + 3.2ns + 0.2ns + 0.6ns
= 4ns
接下来我们要取得Clock2 的锁存沿受延迟的影响。同样TimeQuest模型也使用了一条公式评估 锁存沿受 Tclk2 + Tsu 的影响:
数据锁存(获取|读取)时间 Time Required Time = 锁存沿时间 + Tclk2 - Tsu
= 10ns + 2ns - 1.4ns
= 10.6ns
最后我们要用 数据抵达时间 和 数据锁存时间 取得建立余量:
建立余量 = 数据锁存时间 - 数据抵达(获取|读取)时间
Setup Slack = Time Required Time - Time Arrival Time
= 10.6ns - 4ns
= 6.6ns
其中建立余量 6.6ns 是在图1.5.2的“蓝色框图的部分”。在这里,建立余量是“正值”,亦即“reg1和reg2之间的建立关系是合格”。可能读者会觉得纳闷:“建立余量正值和reg1与reg2之间的建立关系合不合格到底有什么关系?” 呵呵,这真是一个好问题 ... 就让笔者慢慢解释:
图1.5.3 一个例子
图1.5.3 是一个典型的例子,就是reg1向reg2发送数据,reg2从reg1锁存数据。我们先假设 reg1 和 reg2 拥有相同性质的时钟源,然后 reg2 包含一个“可以随意调整”的Tsu。
图1.5.4 加上Tsu延迟因素
Tsu表示了锁存方的寄存器在读取数据之前所需要的“最小准备时间”,图1.5.4中的理建立关系值是10ns,假设为2ns ... 锁存沿从原本10ns的位置返回8ns的位置,那么建立余量从10ns慢慢减至8ns。结果建立余量还是正值,而锁存沿还顶着数据。
图1.5.5 延迟因素 Tsu 调大一点
如图1.5.5所示,假设在把 Tsu调大至3ns,锁存沿从原本10ns的位置返回7ns的位置,那么建立余量也从原本的 8ns的再降至 7ns,不过建立余量还是正值。换言之,只要建立余量还是正值,寄存器2读取Reg1-Q的数据也是没有问题的。
图1.5.6 还是把 Tsu 调大一点
图1.5.6中的 Tsu再再假设调大至 4ns,锁存沿从原本10ns的位置返回6ns的位置,那么建立余量也从原本的 7ns降至6ns。不过建立余量的结果还是正值,如果寄存器2锁存数据,也是没问题的说 ... 总结说,只要建立余量大于0,那么两个寄存器之间的建立关系就没有问题。
===================================================================
经过几番理解,读者是不是对“建立关系值”有一点头绪了?在理想的情况下,建立余量一定是理想的建立关系值。此外,这个理想的建立关系值还有简化公式的作用:
在前面,我们知道为了计算建立余的公式是:
建立余量 = 数据锁存(获取|读取)- 数据抵达时间
其中数据锁存(获取|读取)时间的公式是 :
数据锁存(获取|读取)时间 = 锁存沿时间 + Tclk2 - Tsu
读者知道吗?锁存沿时间基本上就是“理想的建立关系值”。同学们可能会觉得笔者在胡扯,很好!就让笔者尝试用几个例子来解释这一点。
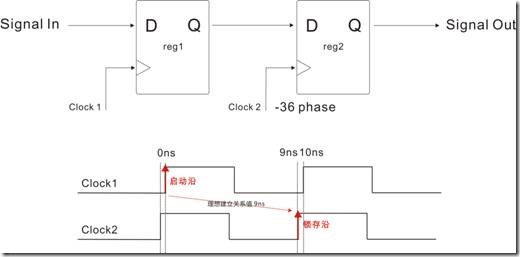
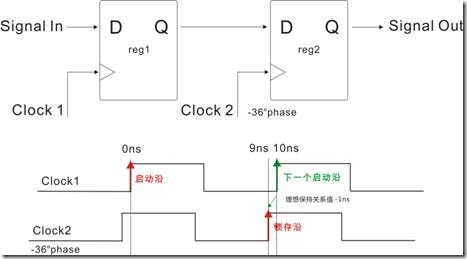
图1.5.7 Clock2位移 -36度
图1.5.7中的Clock1没有变化,换之Clock2位移 -36度,亦即Clock2比起Clock1提早1ns。 Clock2移位 -36度又意味着什么呢?它意味着Clock1和Clock2的理想建立关系值已经改变了,结果为9ns。
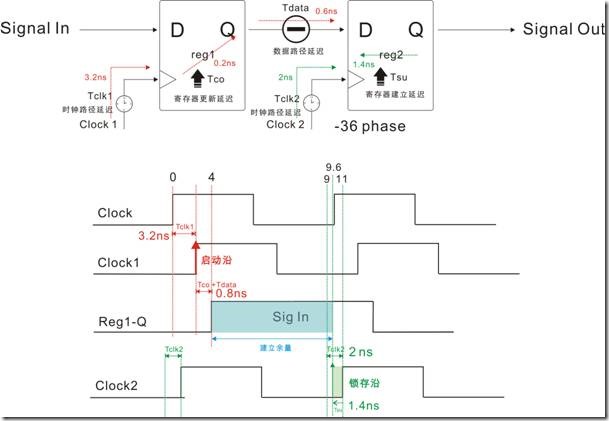
图1.5.8 Cock2经过-36度位移的物理时序图
图1.5.8是图1.5.7物理的建立关系过程,在前面我们知道 Clock1 和 Clock2 之间的理想建立关系值是9ns ...
数据抵达时间 Time Arrival Time = 启动沿时间 + Tclk1 + Tco + Tdata
= 0ns + 3.2ns + 0.2ns + 0.6ns
= 4ns
数据锁存(获取|读取)时间 Time Required Time = 锁存沿时间 + Tclk2 - Tsu
= 9ns + 2ns - 1.4ns
= 9.6ns
建立余量 = 数据锁存时间 - 数据抵达(获取|读取)时间
Setup Slack = Time Required Time - Time Arrival Time
= 9.6ns - 4ns
= 5.6ns
我们取得5.6ns的建立余量,亦即建立关系合格。在这里稍微注意一下锁存沿时间的9ns,结果是不是和理想建立关系值的9ns一模一样呢?读者:“慢着慢着 ... 我差点就要被笔者忽悠了 ... 笔者这样说是不是太扯了!?还是不相信吗?那好,笔者再举另一个例子,这回请看好呀。
===================================================================
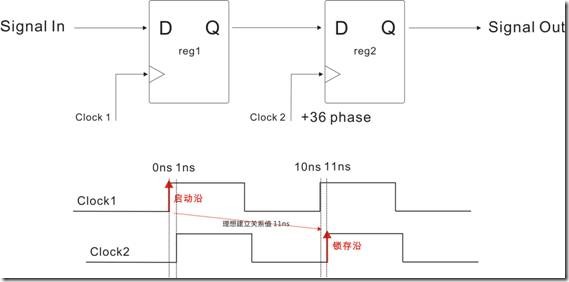
图1.5.9 Clock2位移+36度
图1.5.9 是Clock2 位移+36°,也就是延迟了1ns,这也使得Clock1对应 Clock2的理想建立关系值是11ns。
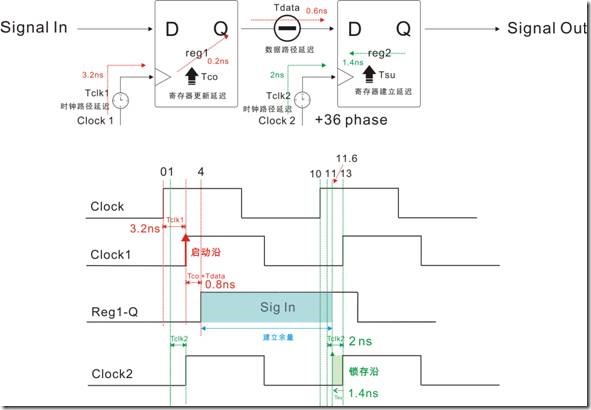
图1.5.10 Cock2经过+36度位移的物理时序图
图1.5.10是Clock2经过+36度位移后的物理建立关系过程,然而理想的建立关系值是 11ns。在这里,我们计算建立余量之余,也看看理想建立关系值是不是和锁存沿时间等价?
数据抵达时间 Time Arrival Time = 启动沿时间 + Tclk1 + Tco + Tdata
= 0ns + 3.2ns + 0.2ns + 0.6ns
= 4ns
数据锁存(获取|读取)时间 Time Required Time = 锁存沿时间 + Tclk2 - Tsu
= 11ns + 2ns - 1.4ns
= 11.6ns
建立余量 = 数据锁存时间 - 数据抵达(获取|读取)时间
Setup Slack = Time Required Time - Time Arrival Time
= 11.6ns - 4ns
= 7.6ns
有没有看到?理想建立关系值和锁存沿时间在评估数据锁存时间是等价的关系 ... 当然理想建立关系值的作用不仅而已,它作用还偶用来“评估”建立余量。在原理上“建立余量是不可能超过理想建立关系值”,如果超过了,那么两个节点(寄存器)之间的建立关系就违规,或者不合格化了。
1.6 保持余量
“保持时间”在寄存器的概念中是表示:寄存器在读取某个数据以后,需用一段最小时间来“确保数据锁存”的稳定。然而“保持余量”的定义是指:在两个节点(寄存器)之间,在分析保持关系的过程中“到底有多少剩时间可以提供给寄存器用来确保已存数据的稳定”。嗯 ... 同学们是不是开始抓狂了?那么我们来看一副图 ...
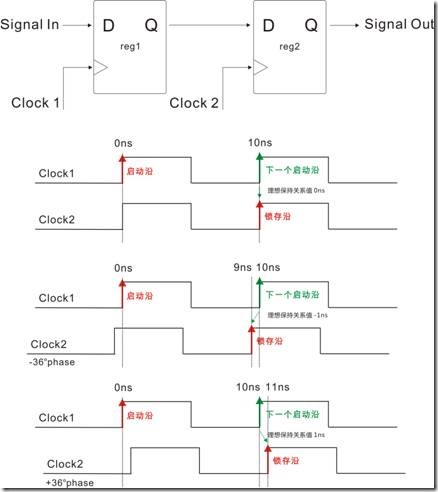
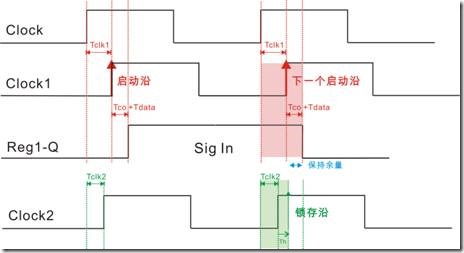
图1.6.1 不同的理想保持关系值
让我们先回忆一下,如何取得“理想保持关系值”... 亦即下一个启动沿和当前锁存沿之间的距离。图1.6.1中呈现不同的理想保持关系值,笔者曾说过 ... 只有当 Clock1 和 Clock2使用相同性质的时钟的时候,理想的保持关系值才是0ns。当Clock2有-36度的位移,亦即Clock2比起Clock1提早1ns,那么理想保持关系值是 -1ns。又当CLock2有+36度的位移,亦即Clock2比起Clock1延迟1ns,那么理想保持关系值是 1ns。
其中“这个 0ns,-1ns,+1ns理想保持关系值”到底对取得保持余量有什么作用呢?
在这里笔者需要强调一下!保持余量在英文中 Hold Slack,然而保持关系 Hold Relationship是求出两个寄存器(节点)之间的保持余量的过程。
1. 这个“0ns,-1ns,1ns” ≠ Hold Relationship。
2. 这个“0ns,-1ns,1ns”是一个理想值而已。
3. 这个“0ns,-1ns,1ns”理想值,在 Hold Relaionship 的过程中“保持余量”的参考值而已!
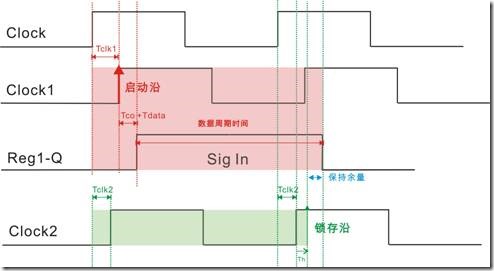
图1.6.2 在物理保持关系中出现的延迟因数
笔者也在前面好像说过:“保持关系是指寄存器1在还没有更新输出之前,寄存器2用最快速的速度读取从寄存器1发送过来的数据”。在理想的时序图中“理想的保存时间”都是0ns,然而“理想保持关系值”却不是“理想的保存时间”。理想保持关系值是指,在理想状态下,在两个寄存器之间得到的一个可以参考的值而已。
图1.6.2是物理建立关系过程,在两个寄存器(节点)之间的保持关系中有许多延迟因数。Tclk1是寄存器1时钟源的路径延迟,Tco是寄存器1更新数据的时候,最小的消耗时间,Tdata是寄存器1向寄存器2发送数据时最小的数据路劲延迟,Tclk2是寄存器2时钟源的路径延迟,最后的Th是寄存器2用来确保已存数据的最小时间。
TimeQuest模型也用了一条公式评估 启动沿受 Tclk1 + Tco + Tdata 延迟因数的影响:
数据保持时间Data Hold Time = 启动沿 + Tclk1 + Tco + Tdata + 数据周期时间
再来 TimeQuest模型同样也用一条公式评估 锁存沿受 Tclk2 + Th 延迟因素的影响:
数据锁存(读取|获取)时间 Data Required Time = 锁存沿 + Tclk2 + Th
不知同学们有没有注意到,图1.6.2中的Th 出现微妙的箭头方向?在前面的内容中,如果箭头是 ← 会使得锁存沿向左位移,如果箭头是 →,是不是会使得锁存沿向右位移呢?呵呵 ... 接下来我们来看物理时序图:
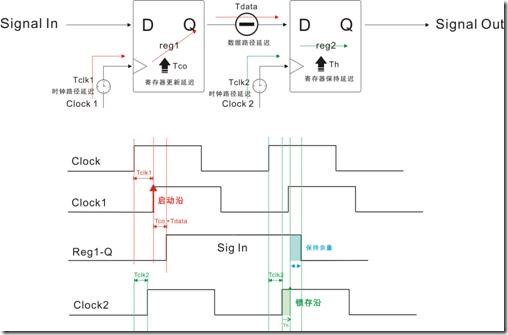
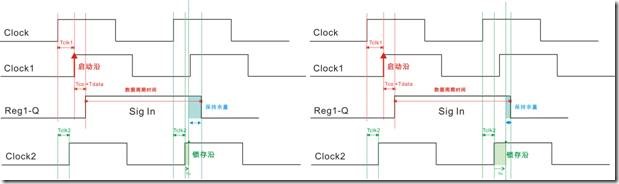
图1.6.3 存在延迟因素的保持关系过程
图1.6.3是物理的保持关系过程和相关的时序图,红色一方是启动沿受延迟以后的结果,绿色一方是锁存沿受延迟因数的影响,浅蓝色一方是保持余量。那么求得保持余量的公式是:
保持余量 = 数据保持时间 - 数据锁存(获取|读取)时间
感觉这样说太抽象了,笔者还是给图1.6.3 填上数字来得更形象。
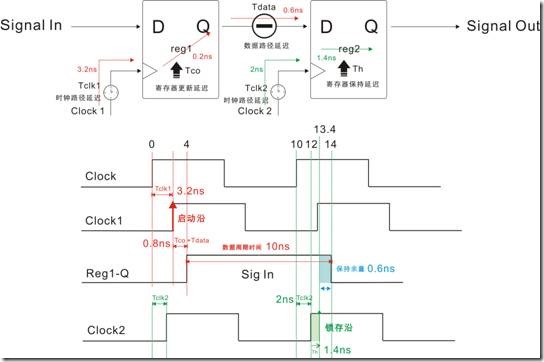
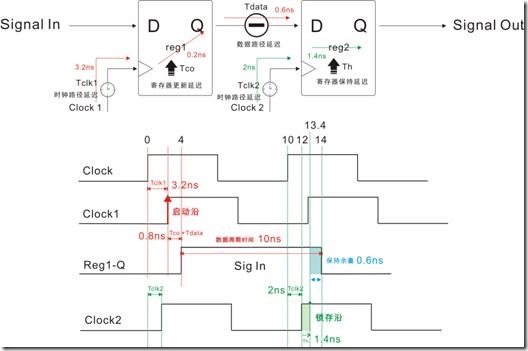
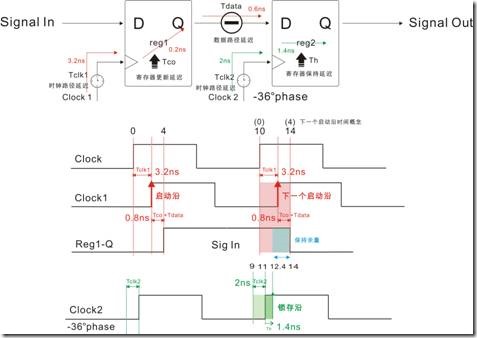
图1.6.4 物理时序与建立余量
数据保持时间Data Hold Time = 启动沿 + Tclk1 + Tco+ Tdata + 数据周期时间
= 0ns + 3.2ns + 0.2ns + 0.6ns + 10ns
= 14ns
数据锁存(读取|获取)时间 Data Required Time = 锁存沿 + Tclk2 + Th
= 10ns + 2ns + 1.4ns
= 13.4ns
保持余量 Hold Slack = 数据保持时间 - 数据锁存(获取|读取)时间
= 14ns - 13.4ns
= 0.6ns
最后取得的保持余量是 0.6ns ... 这也意味着 保持余量是正值,所以寄存器1和寄存器2之间的保持关系是合格的。在这里,读者可能会觉得纳闷:“寄存器之间的保持关系合格化,到底和保持余量有什么关系?”呵呵呵!我们先假设寄存器2的Th延迟因素可以调制的话...
图1.6.5 不同的 Th 和不同的建立余量
图1.6.5 表示了不同的 Th 和 不同的建立余量。同学们还记得建立关系的定义吗?
就是寄存器1发送的数据在更新(更换)之前,寄存器2可用最短的时间去锁存数据。
在此,保持余量除是提供给Th有余时间以外,它还也表示只要保持余量一天还是正值,那么寄存器2在寄存器更换数据之前,寄存器2就有多少可以优哉读取数据的时间。
保持余量的故事就先告一个段落 .. 注意,到目前为止理想保持关系值还没有出场到。
===================================================================
在这里,笔者要告诉告诉读者们一个非常“坏”的消息 ... 一些顽皮的读者估计已经发现到,前面的内容视乎和TimeQuest 的手册,或者官方相关内容是大为不同?甚至怀疑“笔者是不是搞错了?”然后借机寻找笔者的痛脚 ... 嘛,这一切的一切都有深长的因缘 ... 接下来慢慢听笔者解释!
早期在TimeQuest 将近完成之际,有一位师兄说道:
师兄:没日没夜的项目终于要搞一个段落了,非常期待这款软件发出后,会不会给fpga
界一个大惊喜呢?那些第二第三的工程师们,一定要把我当神拜。
忽然间,一位师弟插嘴道。
师弟:老大,你过来看一下 ... 求出建立余量 和 保持余量 的公式 是不是不够和谐?
师兄:怎么不和谐呢?我的设计是接近神级的 ...
师弟:有没有办法把求出建立余量和保持余量的公式凑合凑合,两者可以共用同一个公
式?那么你的设计可以更神一层楼。
师兄:对呀,你怎么不早说,我的世界是没有最完美,只有更完美 ...
就这样,建立余量和保持余量的共用公式就次诞生了。在前面笔者说过“无论是理想的建立关系值或者理想的保持关系值”它们的作用出了供参考以外,还有简化TimeQuest模型。这一句是千真万确的,因为“保持余量”的求出过程实在太猥琐了,在此为了简化求出保持余量的过程,保持余量和建立余量共享同一个公式,那么这个“理想保持关系值”是必须的。
好了,笔者继续以上述的例子为例子:
图1.6.6 理想保持关系
图1.6.6是理想的保持关系过程,而理想的保持关系值既是 0ns。
图1.6.7 求出保持余量的物理时序图
接下来,让我们来看看看建立余量和保持余量如何共享一个公式?
TimeQuest 用了一条公式评估 启动沿受 Tclk1 + Tco + Tdata 延迟因数的影响:
数据抵达时间Data Arrival Time = 启动沿 + Tclk1 + Tco + Tdata
(注意:此时不是数据保持时间 Data Hold Time,所以也没有加入数据周期时间)
TimeQuest 也用了一个条式评估 锁存沿受 Tclk2 + Th 延迟因数的影响:
数据锁存(获取|读取)时间 Data Required Time = 锁存沿 + Tclk2 + Th
= 理想保持关系值 + Tclk2 + Th
(注意:这个评估锁存沿受延迟因素影响的公式和求得建立余量时数据锁存时间的公式非常类似)
那么求得的保持余量是:
保持余量 = 数据抵达时间 - 数据锁存(获取|读取)时间
好了,现在我们套用这个公式求出图 1.6.7 中的保持余量。
数据抵达时间Data Arrival Time = 启动沿 + Tclk1 + Tco + Tdata
= 0 + 3.2 + 0.2 + 0.6
= 4ns
数据锁存(获取|读取)时间 Data Required Time = 锁存沿 + Tclk2 + Th
= 理想保持关系值 + Tclk2 + Th
= 0ns + 2ns + 1.4ns
= 3.4ns
保持余量 = 数据抵达时间 - 数据锁存(获取|读取)时间
= 4ns - 3.4ns
= 0.6ns
咦咦咦?求出的结果确实是一样哦?难道是TimeQuest在变魔术?还是自己眼花了?
同学们我们都没有看错 ... 不错!那是TimeQuest模型的公式戏法。事实上不是TimeQuest 在变魔术,而是TimeQuest模型懒得用头脑求得保持余量,随之就用屁股求得保持余量,这话何解呢?
图1.6.8 用头脑求得保持余量
图1.6.8 是用头脑求得保持余量的方法,也就是说“红色部分的长度 - 绿色部分的长度”,亦即用数据保持时间减掉数据抵达时间。用傻瓜的话来讲,求得保持余量必须从 0ns 开始算起。
图1.6.9 用屁股求得保持余量
图1.6.9是用屁股求得保持余量的方法,换句话说就是“用下一个启动沿的红色部分减掉当前锁存沿绿色的部分”,其中就要用到“理想保持关系值”。如果继续用屁股来解释的话,那么“将启动沿的总和延迟时间减掉锁存沿的总和延迟时间,然后顺便参考一下理想保持关系值”。
啊 .... 同学们别那么惊讶,笔者也只是把事实说出来而已,师兄确实为了使建立余量和保持余量可以共用一个公式,才会开始用屁股想东西。如果同学们还是不相信的话,我们可以用几个例子来实验看看:
图1.6.10 Clock2位移 -36度
图1.6.10 是理想的保持关系过程,其中Clock1对应Clock2的理想保持关系值是 -1ns。而图1.6.11是物理的保持关系过程。
图1.6.11 Clock2位移-36度的物理时序图
好了笔者先用头脑求得保持余量:
保持余量 = 数据保持时间 - 数据锁存(获取|读取)时间
= (启动沿 + Tclk1 + Tco + Tdata + 数据时间周期)-(锁存沿 + Tclk2 + Th)
=(0 + 3.2 + 0.2 + 0.6 + 10)ns -(9 + 2 + 1.4)ns
= 14ns - 12.4ns
= 1.6ns
如果用屁股求得保持余量:
保持余量 = 数据抵达时间 - 数据锁存(获取|读取)时间
=(启动沿 + Tclk1 + Tco + Tdata)-(锁存沿 + Tclk2 + Th)
=(启动沿 + Tclk1 + Tco + Tdata)-(理想保持关系值 + Tclk2 + Th)
=(0 + 3.2 + 0.2 + 0.6)ns -(-1 + 2 + 1.4)ns
= 4ns - 2.4ns
= 1.6ns
在这里,可能有同学要问:“用屁股求得余量为什么启动沿的时间不是10而是0呢?”很简单呀,如果用屁股来求得保持余量,那么下一个启动沿的时间,被视为“重新开始”,亦即0ns 而不是10ns。这一点要好好的记住。
总结:
TimeQuest 说得简单点就是为懒人准备的物理时序分析工具,关于“物理时序分析"的概念就自己维基百科看看吧。其中TimeQuest 有自己的一套“模型”用来分析物理时序从何摆脱猥琐的时序分析工作,但是TimeQuest的模型使用步骤还是一样猥琐不少。
在宏观上TimeQuest 的模型是基于“两个节点”和才能成立。
有关“节点”在TimeQuest模型里的定义有很多很多,但是为了简化笔记的内容笔者就先吧“节点”充当“寄存器”,更多有关节点的故事以后再谈。TimeQuest模型为了确定两个寄存器(节点)之间的时序是合格的,所以用了“建立关系”和“保持关系”的概念。
在理想的状态下“建立关系”有一个理想的建立关系值,反之“保持关系”有一个理想的保持关系值,它们的作用出了提供参考以外,还可以简化TimeQuest模型。“保持关系”和“建立关系”会随着理想时钟源的状态也会产生不同的“理想建立关系值”和“理想保持关系值”。
那么TimeQuest的模型又用“什么方法来确定两个寄存器之间的建立关系和保持关系是合格的呢?”建立关系确保合格的办法就是取得正值的建立余量,同样的保持关系确保合格办法就是取得正值的保持余量。
求得建立余量的公式是 :
保持余量 = 数据锁存时间 - 数据抵达时间
Setup Slack = Data Required Time - Data Arrival Time
数据抵达时间 Data Arrival Time = 启动沿 + Tclk1 + Tco + Tdata
数据获取时间 Data Required Time = 锁存沿 + Tclk2 - Tsu
= 理想建立关系值 + Tclk2 - Tsu
求得保持余量的公式是:(用头脑的话)
保持余量 = 数据保持时间 - 数据获取时间
Hold Slack = Data Hold Time - Data Required TIme
数据保持时间 Data Hold Time = 启动沿 + Tclk1 + Tco + Tdata + 数据周期时间
数据获取时间 Data Required Time = 锁存沿 + Tclk2 + Th
(不要问我数据周期时间如何得到,如果稍微有Verilog HDL语言的时序概念的话,都会知道如何取得。一般上数据周期时间等价于该时钟源的周期时间)
求得保持余量的公式是:(用屁股的话)
保持余量 = 数据抵达时间 - 数据获取时间
Hold Slack = Data Arrival Time - Data Required Time
数据抵达时间 Data Arrival Time = 启动沿 + Tclk1 + Tco + Tdata
数据获取时间 Data Required Time = 锁存沿 + Tclk2 + Th
= 理想保持关系值 + Tclk2 + Th
===================================================================
好了,笔者差不多要结束这一章节的笔记了。这一章,笔者只是单纯又简单的讲解:
“学习TimeQuest模型的概念时容易陷入的几个灰区而已”。
此外,笔者也大概的讲解TimeQuest模型中用到的公式和物理时序中出现的东东。如果按照一般方法去学习TimeQuest的话,很容易撞墙而已,又或者会被训练成为纯公式的使用者。TimeQuest模型是一个很有趣的东西,如果用纯公式的方法去使用的话,就无法体验到TimeQuest的有趣之处以外,也不能享受学习的乐趣。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号