The 2025 ICPC Asia Chengdu Regional Contest

B

现在有\(n\)个人（\(n\leq 6\)），每个人有一个伤害值\(a_i\)和魔力消耗\(c_i\)，在一个回合中，总共可以使用魔力值为\(m\)，每一回合的魔力值都会重置为\(m\)，如果上一回合使用了第\(i\)个人，那么这一回合再使用第\(i\)个人的魔力消耗为\(c_i+k\)，求\(R\)回合能够造成的最大伤害。

\(R\leq 1e9\)

其实可以很容易的写出\(f_{i,s}=\max_{\sum_{i\in s}{a_i}+popcount(s\&t)\times k\leq m}{(f_{i-1,t}+A_s)}\)，其中\(A_s\)表示选择人的状态为\(s\)能够造成的伤害，即\(A_s=\sum_{i\in s}{a_i}\)。总状态数为\(R\times 2^n\)，每次转移的时间复杂度为\(O(2^n)\)，总时间复杂度为\(O(4^n\times R)\)，是会超时的。

考虑状态\(f_{i,s}\)，它只有前一轮的状态\(t\)决定，因为我们可以预处理\(G[i][j]\)，表示上一轮状态为\(i\)，这一轮状态为\(j\)时增加的伤害。改变上面的式子为\(f_{i,s}=\max{f_{i-1,t}+G[t][s]}\)，我们怎样快速的求出\(f_{i,s}\)呢？可以使用矩阵快速幂。

\(dp^{1}[i][j]\)表示初始状态\(i\)，结束状态为\(j\)经过一回合的最大伤害；
\(dp^{2}[i][j]\)表示经过两个回合的最大伤害，这个我们可以通过枚举中间状态\(k\)，\(dp^2[i][j]=dp^1[i][k]\times dp^1[k][j]\)，也就是枚举中间经过的这一轮，因为\(dp^1[i][j]\)我们在前面已经求过了；
\(dp^4[i][j]\)则可以通过\(dp^2[i][k]\times dp^2[k][j]\)来求得；

所以我们可以用矩阵快速幂来优化\(dp\)，使得最终复杂度为\(O(8^n\times \log{R})\)。

#include <bits/stdc++.h>
using namespace std;
#define inf 1e18
#define endl '\n'
#define int long long
typedef  long long ll;
typedef pair<int, int> pii;
int dx[4] = {1, 0, -1, 0}, dy[4] = {0, 1, 0, -1};
const int N = 2e5 + 9, M = 2e5 + 9, mod = 1e9 + 7;
vector<vector<int>> operator*(vector<vector<int>> &A,vector<vector<int>> &B){
	int n=A.size();
	vector<vector<int>> res(n,vector<int>(n));
	for(int k=0;k<n;k++){
		for(int i=0;i<n;i++){
			for(int j=0;j<n;j++){
				res[i][j]=max(res[i][j],A[i][k]+B[k][j]);
			}
		}
	}
	return res;
}
void solve() {
	int n,m,k,R;
	cin >> n >> m >> k >> R;
	vector<int> a(n+1),c(n+1);
	for(int i=1;i<=n;i++){
		cin >> a[i] >> c[i];
	}
	//预处理M[i][j]表示状态i到j的增量
	vector<vector<int>> M(1<<n,vector<int>(1<<n,0));
	for(int i=0;i<(1<<n);i++){
		for(int j=0;j<(1<<n);j++){
			int suma=0,sumc=0;
			for(int t=0;t<n;t++){
				if(j>>t&1){
					suma+=a[t+1];
					sumc+=c[t+1];
					if(i>>t&1) sumc+=k;
				}
			}
			if(sumc<=m){
				M[i][j]=suma;
			}
		}
	}
	vector<vector<int>> Mr(1<<n,vector<int>(1<<n,0));
	while(R){
		if(R&1) Mr=Mr*M;
		M=M*M;
		R>>=1;
	}
	int ans=0;
	for(int i=0;i<(1<<n);i++){
		for(int j=0;j<(1<<n);j++){
			ans=max(ans,Mr[i][j]);
		}
	}
	cout << ans << endl;
}
/*

*/
signed main() {
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	int t = 1;
	cin >> t;
	while (t--) {
		solve();
	}
	return 0;
}

L

给定一棵有根树，现在每个节点有两个属性\(a_i\)和\(b_i\)，对于\(u\)的一棵子树，我们可以交换子树上的\(a\)，来让最后\(u\)的子树上的每个节点的\(a_i=b_i\)，特别地，如果\(a_i=0\or b_i=0\)，那么也是可以配对的，也就是说\(0\)是通配符。现在我们要独立的求出每棵子树是否都可以通过交换操作让\(a_i\)和\(b_i\)配对，交换操作是独立的，也就是不会影响另一棵子树的求解。

首先因为是可以任意交换\(a\)的，因此\(b\)可以对应\(a\)的任何一个排列，所以相当于\(a\)和\(b\)都可以交换。

考虑求解\(u\)这棵子树的答案，我们需要对这棵子树维护一个\(cnt\)数组以及一个\(sum\)，用来记录值为\(cnt_i\)的个数，具体操作就是：

对于\(a_j=i\)，\(cnt_i:=cnt_i+1\)。维护\(sum\)时，我们根据\(cnt_i\)的大小来判断，如果\(cnt_i\geq 0\)，那么\(sum:=sum+1\)，否则\(sum:=sum-1\)；
对于\(b_j=i\)，\(cnt_i:=cnt_i-1\)。维护\(sum\)时，如果\(cnt_i> 0\)，那么\(sum:=sum-1\)，否则\(sum:=sum+1\)；

特别地，对于\(i=0\)，我们只执行\(cnt_0:=cnt_0+1,sum:=sum+1\)。

这样一棵子树是否可以完全匹配，可以通过判断\(sum-cnt_0\leq cnt_0\)来判断，也就是非0的个数要小于0的个数，那么也就可以完全匹配。

检查一棵子树的时间复杂度为\(O(n)\)，如果对每个节点都\(dfs\)一次，时间复杂度变成\(O(n^2)\)，不能接收，我们考虑检查完子树后，同时把信息上传，这就可以用到树上启发式合并，也是新学的内容，非常的叼，对于需要合并子树信息的，可以达到时间复杂度\(O(n\log{n})\)，适用于只询问，不修改。

树上启发式合并的操作流程：

重链剖分，求出重儿子；
\(dfs(u,keep)\)，表示操作子树\(u\)，如果\(keep=0\)，那么要撤销子树\(u\)的影响；否则保留子树\(u\)的信息。
- 先访问\(u\)的轻儿子；
- 再访问\(u\)的重儿子；
- 加上\(u\)节点自己的贡献；
- 再次访问\(u\)的轻儿子，可以使用一个\(add\)函数，专门来加上贡献；
- 求解\(u\)的答案；
- 根据\(keep\)，判断\(u\)的信息是否保留，如果撤销，专门用函数\(del\)来撤销；
有一个性质是，我们在撤销轻儿子贡献的时候，可以直接对\(cnt[a[u]]:=0,cnt[b[u]]:=0,sum:=0\)，因为在访问轻儿子的时候，\(cnt\)数组一定是空的。

这里可以浅谈一下为什么时间复杂度会是\(O(n\log{n})\)，根据上面操作，我们看到多出的部分主要是再次访问轻儿子以及撤销轻儿子的贡献，这两个是互逆的，所以我们就看再次访问轻儿子的次数。

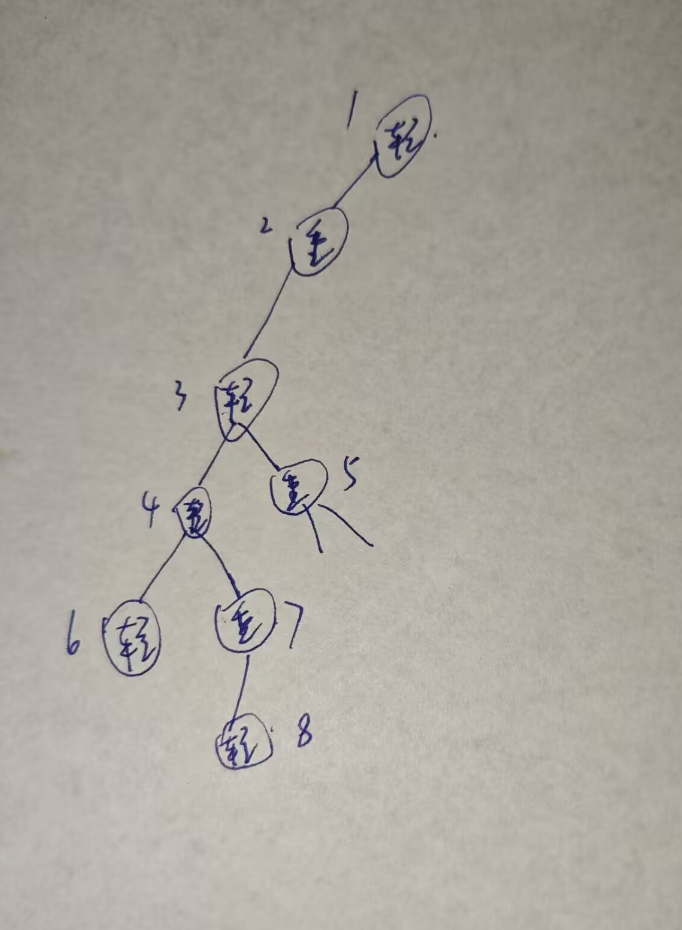
我们看8号节点，开始自己是轻儿子，那么需要撤销一次，当回溯到4号节点时，因为4是轻儿子，所以8又要被撤销一次，遇到3被撤销一次，遇到1被撤销一次。我们可以看到只有当遇到轻儿子的时候，节点才会被撤销，但是这个轻儿子和旁边重儿子合并，相当于节点数量至少是轻儿子子树大小的两倍，那么也就是每次遇到轻儿子，那么这个轻儿子大小乘以2，那么最多可以遇到多少个轻儿子呢，也就是\(\log_2{n}\)次，所以8号节点撤销的次数不会超过\(\log{n}\)，所以时间复杂度大概为\(O(n\log{n})\)。

一发就过，爽！！！

void solve() {
	int n;
	cin >> n;
	vector<int> a(n+1),b(n+1);
	for(int i=1;i<=n;i++){
		cin >> a[i];
	}
	for(int i=1;i<=n;i++){
		cin >> b[i];
	}
	vector<vector<int>> tr(n+1);
	for(int i=1;i<n;i++){
		int u,v;cin >> u >> v;
		tr[u].push_back(v);
		tr[v].push_back(u);
	}
	vector<int> cnt(n+1),ans(n+1);
	vector<int> siz(n+1),son(n+1),fa(n+1);
	int sum=0;
	auto go=[&](int u)->void{
		if(a[u]==0){
			cnt[a[u]]++;
			sum++;
		}else if(cnt[a[u]]>=0){
			cnt[a[u]]++;
			sum++;
		}else{
			cnt[a[u]]++;
			sum--;
		}
		if(b[u]==0){
			cnt[b[u]]++;
			sum++;
		}else if(cnt[b[u]]<=0){
			cnt[b[u]]--;
			sum++;
		}else{
			cnt[b[u]]--;
			sum--;
		}	
	};
	auto dfs1=[&](auto&& self,int u,int p)->void{
		siz[u]++;
		fa[u]=p;
		for(int v:tr[u]){
			if(v==p) continue;
			self(self,v,u);
			siz[u]+=siz[v];
			if(siz[v]>siz[son[u]]){
				son[u]=v;
			}
		}
	};
	auto del=[&](auto&&self,int u)->void{
		cnt[a[u]]=0;
		cnt[b[u]]=0;
		sum=0;
		for(int v:tr[u]){
			if(v==fa[u]) continue;
			self(self,v);
		}
	};
	auto add=[&](auto&&self,int u)->void{
		go(u);
		for(int v:tr[u]){
			if(v==fa[u]) continue;
			self(self,v);
		}
	};
	auto dfs2=[&](auto&& self,int u,int keep)->void{
		for(int v:tr[u]){
			if(v==fa[u]||v==son[u]) continue;
			self(self,v,0);
		}
		if(son[u]) self(self,son[u],1);
		//添加节点u的贡献
		go(u);
		for(int v:tr[u]){
			if(v==fa[u]||v==son[u]) continue;
			add(add,v);
		}
		if(sum-cnt[0]<=cnt[0]) ans[u]=1;
		if(keep==0) del(del,u);
	};
	dfs1(dfs1,1,0);
	dfs2(dfs2,1,0);
	for(int i=1;i<=n;i++){
		cout << ans[i];
	}
	cout << endl;
}

法二：\(dfs\)序+莫队：

基于我们上面的分析，维护\(cnt\)数组和\(sum\)都是\(O(1)\)的。我们跑一遍\(dfs\)，给每个节点编一个\(dfn\)序，这样对于一棵子树上的问题，在原数组上一定是一块连续的子段\([L,R]\)，那么总共可以得到\(n\)个子段，我们要维护每个子段的信息，因此可以用离线+莫队来做，时间复杂度为\(O(n\sqrt{n})\)，对于\(\sum{n}\leq 2e5\)，是可以接受的。

void solve() {
	int n;
	cin >> n;
	vector<int> a(n+1),b(n+1);
	for(int i=1;i<=n;i++){
		cin >> a[i];
	}
	for(int i=1;i<=n;i++){
		cin >> b[i];
	}
	vector<vector<int>> tr(n+1);
	for(int i=1;i<n;i++){
		int u,v;cin >> u >> v;
		tr[u].push_back(v);
		tr[v].push_back(u);
	}
	vector<int> ans(n+1),cnt(n+1);
	int sum=0;
	vector<int> dfn(n+1);
	int tot=0;
	vector<array<int,3>> seg(n+1);//seg[u]表示u管辖的范围
	auto dfs1=[&](auto&& self,int u,int p)->void{
		dfn[u]=++tot;
		for(int v:tr[u]){
			if(v==p) continue;
			self(self,v,u);
		}
	};
	auto dfs2=[&](auto&& self,int u,int p)->void{
		seg[u]={dfn[u],dfn[u],u};
		for(int v:tr[u]){
			if(v==p) continue;
			self(self,v,u);
			seg[u][0]=min(seg[u][0],seg[v][0]);
			seg[u][1]=max(seg[u][1],seg[v][1]);
		}
	};
	dfs1(dfs1,1,0);
	dfs2(dfs2,1,0);
	vector<int> mp(n+1);
	for(int i=1;i<=n;i++){
		mp[dfn[i]]=i;//建立反向索引
	}
	int sq=sqrt(n);
	sort(seg.begin()+1,seg.end(),[&](array<int,3> x,array<int,3> y){
		auto[l1,r1,idx1]=x;
		auto[l2,r2,idx2]=y;
		if(l1/sq!=l2/sq) return l1/sq<l2/sq;
		else return r1<r2;
	});
	auto go=[&](int u)->void{
		if(a[u]==0){
			cnt[a[u]]++;
			sum++;
		}else if(cnt[a[u]]>=0){
			cnt[a[u]]++;
			sum++;
		}else{
			cnt[a[u]]++;
			sum--;
		}
		if(b[u]==0){
			cnt[b[u]]++;
			sum++;
		}else if(cnt[b[u]]<=0){
			cnt[b[u]]--;
			sum++;
		}else{
			cnt[b[u]]--;
			sum--;
		}	
	};
	int cl=1,cr=0;
	for(int i=1;i<=n;i++){
		auto[l,r,id]=seg[i];
		while(l<cl) go(mp[--cl]);
		while(r>cr) go(mp[++cr]);
		while(cl<l) go(mp[cl++]);
		while(cr>r) go(mp[cr--]);
		if(sum-cnt[0]<=cnt[0]) ans[id]=1;
	}
	for(int i=1;i<=n;i++){
		cout << ans[i];
	}
	cout << endl;
}

这里的\(go(u)\)还有点问题。

修改了一下，改成了\(add\)和\(del\)：

void solve() {
	int n;
	cin >> n;
	vector<int> a(n+1),b(n+1);
	for(int i=1;i<=n;i++){
		cin >> a[i];
	}
	for(int i=1;i<=n;i++){
		cin >> b[i];
	}
	vector<vector<int>> tr(n+1);
	for(int i=1;i<n;i++){
		int u,v;cin >> u >> v;
		tr[u].push_back(v);
		tr[v].push_back(u);
	}
	vector<int> ans(n+1),cnt(n+1);
	int sum=0;
	vector<int> dfn(n+1);
	int tot=0;
	vector<array<int,3>> seg(n+1);//seg[u]表示u管辖的范围
	auto dfs1=[&](auto&& self,int u,int p)->void{
		dfn[u]=++tot;
		for(int v:tr[u]){
			if(v==p) continue;
			self(self,v,u);
		}
	};
	auto dfs2=[&](auto&& self,int u,int p)->void{
		seg[u]={dfn[u],dfn[u],u};
		for(int v:tr[u]){
			if(v==p) continue;
			self(self,v,u);
			seg[u][0]=min(seg[u][0],seg[v][0]);
			seg[u][1]=max(seg[u][1],seg[v][1]);
		}
	};
	dfs1(dfs1,1,0);
	dfs2(dfs2,1,0);
	vector<int> mp(n+1);
	for(int i=1;i<=n;i++){
		mp[dfn[i]]=i;//建立反向索引
	}
	int sq=sqrt(n);
	sort(seg.begin()+1,seg.end(),[&](array<int,3> x,array<int,3> y){
		auto[l1,r1,idx1]=x;
		auto[l2,r2,idx2]=y;
		if(l1/sq!=l2/sq) return l1/sq<l2/sq;
		else return r1<r2;
	});
	auto add=[&](int u)->void{
		if(a[u]==0){
			cnt[a[u]]++;
			sum++;
		}else if(cnt[a[u]]>=0){
			cnt[a[u]]++;
			sum++;
		}else{
			cnt[a[u]]++;
			sum--;
		}
		if(b[u]==0){
			cnt[b[u]]++;
			sum++;
		}else if(cnt[b[u]]<=0){
			cnt[b[u]]--;
			sum++;
		}else{
			cnt[b[u]]--;
			sum--;
		}
	};
	auto del=[&](int u)->void{
		if(a[u]==0){
			cnt[a[u]]--;
			sum--;
		}else if(cnt[a[u]]>0){
			cnt[a[u]]--;
			sum--;
		}else{
			cnt[a[u]]--;
			sum++;
		}
		if(b[u]==0){
			cnt[b[u]]--;
			sum--;
		}else if(cnt[b[u]]<0){
			cnt[b[u]]++;
			sum--;
		}else{
			cnt[b[u]]++;
			sum++;
		}
	};
	int cl=1,cr=0;
	for(int i=1;i<=n;i++){
		auto[l,r,id]=seg[i];
		while(l<cl) add(mp[--cl]);
		while(r>cr) add(mp[++cr]);
		while(cl<l) del(mp[cl++]);
		while(cr>r) del(mp[cr--]);
		if(sum-cnt[0]<=cnt[0]) ans[id]=1;
	}
	for(int i=1;i<=n;i++){
		cout << ans[i];
	}
	cout << endl;
}

posted @ 2025-11-28 13:59 alij 阅读(0) 评论(0) 收藏举报

刷新页面返回顶部

alij

The 2025 ICPC Asia Chengdu Regional Contest

B

L

公告