牛客周赛 Round 100
A题
题意:构造一个双排列,直接输出就好,保证\(1\)到\(n\)每个数出现了两次,直接从\([1,2\times n]\)枚举\(i\),输出\((i+1)/2\)即可。
B题
题意:给定一个\(2\times n\)的双排列,现在要输出两个不重叠的子序列,且子序列是长度为\(n\)的排列,那么可以用一个\(pos\)数组记录\(1\)到\(n\)第一次出现的位置,即\(pos[i]\)表示数字\(i\)第一次出现的位置,那么这样我们可以从双排列中选到第一个子序列,之后再次枚举没有被选过的位置就可以了。
3 1 1 2 3 2
第一次选择
3 1 2
1 3 2
C题
\(\hspace{15pt}\)小红拿到了一个长为 \(2\times n\) 的双排列 \(\{a_{1},a_{2},...,a_{2\times n}\}\) 。
\(\hspace{15pt}\)小芳能帮他进行任意次如下操作:
\(\hspace{23pt} \bullet\) 选择一个首尾元素相等的区间 \(\left[l,r\right]\left(1 \leqq l < r \leqq 2\times n;\ a_{l} = a_{r}\right)\) ,将 \(a_{l},a_{l+ 1},...,a_{r}\) 这段元素删除,并将其余元素按现有顺序拼接起来。
\(\hspace{15pt}\)小红想知道,在可以进行任意次上述操作的情况下,能否将双排列中的所有数删除。
【名词解释】
\(\hspace{15pt}\)双排列:长度为 \(2\times n\) 的双排列为两个长度为 \(n\) 的排列打乱顺序后得到的数组。
\(\hspace{15pt}\)排列:长度为 \(n\) 的排列是由 \(1,2,\dots,n\) 这 \(n\) 个整数、按任意顺序组成的数组(每个整数均恰好出现一次)。例如,\(\{2,3,1,5,4\}\) 是一个长度为 \(5\) 的排列,而 \(\{1,2,2\}\) 和 \(\{1,3,4\}\) 都不是排列,因为前者存在重复元素,后者包含了超出范围的数。
题意:每次操作选择两个下标\(l,r\),且\(l \not= r,a[l]==a[r]\),然后删除这一段区间,也就是每次可以选择两个相等的元素,之后删除它们之间的所有元素,问是否可以将这个双排列全部删除。
我们考虑删除某一个值\(x\),如果有\(a[i]==a[j]==x,i<j\),那么要删除\(x\),有两种情况:直接删除区间\([i,j]\);或者考虑是否存在一个更大的区间\([m,n]\)恰好能够包含区间\([i,j]\),如果存在,那么通过删除区间\([m,n]\)同时也可以将\(x\)删除,但是这种情况也可以先删除区间\([i,j]\),不会影响区间\([m,n]\)的删除,如果不存在,也就是第一种情况直接删除区间\([i,j]\)才能删除值\(x\)。从上面两种情况来看无论是否直接删除元素\(x\)或者通过更大的区间删除\(x\),我们都可以直接删除配对的一个区间端点\(i,j\)。
因此我们从前往后枚举,同时用一个栈来维护还没有删掉的元素,用\(vis[x]\)表示元素\(x\)是否在栈中。对于下标\(i\),如果\(vis[a[i]]==1\),那么我们就不断出栈,将栈顶元素标记\(vis[st.top()]=0\),直到元素\(a[i]\)出栈。最后我们只需要判断栈中是否还存在元素即可。
还有另外一种考虑方式是:我们先考虑\(a[1]\),因为它只能通过自己来删除,所以我们可以先删除区间\([1,r](a[1]==a[r])\),然后第\(r+1\)个元素又变为了第一个元素,那么做相同的处理。判断不能全部删除就是"第一个"元素配对的元素的下标小于当前下标。
void solve(){
int n;cin >> n;
vector<int> a(2*n+1),vis(n+1,0);
stack<int> st;
for(int i=1;i<=2*n;i++){
cin >> a[i];
}
for(int i=1;i<=2*n;i++){
if(vis[a[i]]){
while(st.size()&&vis[a[i]]){
vis[st.top()]=0;
st.pop();
}
}else{
st.push(a[i]);
vis[a[i]]=1;
}
}
if(st.size()) cout << "No" << endl;
else cout << "Yes" << endl;
}
D题
\(\hspace{15pt}\)对于给定的长度为 \(2 \times m\) 的双排列 \(\{b_{1},b_{2},...,b_{2\times m}\}\),对于每个 \(k\),若其两次出现的位置为 \(l\) 和 \(r\left(1\leqq l<r\leqq 2\times m\right)\),则定义 \(f\left(k\right) = r - l - 1\)。
\(\hspace{15pt}\)小红将双排列的权值定义为每一对相同元素的下标距离之和,即:
\(\sum\limits_{i = 1}^{m}{f\left(i\right)}\) 。
\(\hspace{15pt}\)现在小红拿到了一个长为 \(2 \times n\) 的双排列 \(\{a_{1},a_{2},...,a_{2\times n}\}\)。
\(\hspace{15pt}\)小芳可以帮他进行最多一次如下操作(也可以不操作):
\(\hspace{23pt}\bullet\)选择下标 \(l, r \ (1 \leqq l, r \leqq 2 \times n)\),交换 \(a_{l}, a_{r}\)。
\(\hspace{15pt}\)请你帮小红求出可得到的最大权值。
题意:现在可以选择一对下标\(i,j\)进行交换,问通过这个操作,小红可以得到的最大权值。
由于是交换一对下标\(i,j\),如果\(a[i]==a[j]\),那么相当于没有操作,也就是原数组的权值;如果\(a[i]\not= a[j]\),那么肯定会影响两个元素\(x,y\)。我们考虑这两个元素之间的位置关系,可以有下面几种情况:
x...y...x...y
x...x...y...y
x...y...y...x
y放第一个位置是一样的,因为我们计算的是位置相减
可以发现上面第1种和第三种不管怎么移动,结果都不会改变,而第二种移动可以增大权值。
所以考虑第二种如何移动?但是你会发现只要x和y交换,不管是第一个还是第二个y,两种情况计算出的权值是一样的,所以只要x和y发生交换就行。
那么我们知道了要找到\(xx...yy\)这样形式的,发生交换才有用,那么要想增加的更多,肯定是最左边第一次出现的\(xx\)和最右边第一次出现的\(yy\),它们发生交换能够最大化权值。
所以我们去找到\(xx\)中的第二个\(x\)出现的位置\(first\),和\(yy\)第一个\(y\)出现的位置\(last\),如果\(first<last\),那么交换即可,否则不操作。最后求一下操作完之后数组的权值即可。
void solve(){
int n;cin >> n;
vector<int> a(n*2+1),vis(n+1,0);
for(int i=1;i<=2*n;i++){
cin >> a[i];
}
int first=0,last=0;
for(int i=1;i<=2*n;i++){
if(!vis[a[i]]){
vis[a[i]]=1;
}else{
first=i;
break;
}
}
for(int i=1;i<=n;i++) vis[i]=0;
for(int i=2*n;i>=1;i--){
if(!vis[a[i]]){
vis[a[i]]=1;
}else{
last=i;
break;
}
}
if(first<last){
swap(a[first],a[last]);
}
// for(int i=1;i<=2*n;i++) cout << a[i] << " ";
// cout << endl;
int ans=0;
vector<int> pos(n+1);
for(int i=1;i<=n;i++) vis[i]=0;
for(int i=1;i<=2*n;i++){
if(!vis[a[i]]){
pos[a[i]]=i;
vis[a[i]]=1;
}else{
ans+=i-pos[a[i]]-1;
}
}
cout << ans << endl;
}
E题
\(\hspace{15pt}\)小红拿到了一个长为 \(2\times n\) 的双排列 \(\{a_{1},a_{2},...,a_{2\times n}\}\) 。
\(\hspace{15pt}\)小芳能帮他进行任意次如下操作:
\(\hspace{23pt}\bullet\)选择一个首尾元素相等的区间 \(\left[l,r\right]\left(1 \leqq l < r \leqq 2 \times n;\ a_{l} = a_{r}\right)\) ,将 \(a_{l},a_{l+ 1},...,a_{r}\) 这段元素删除,并将其余元素按现有顺序拼接起来,同时小红将获得 \(\sum\limits_{i = l}^{r}{a_{i}}\) 分。
\(\hspace{15pt}\)请你帮小红求出可能的最高得分。
题意:选择区间\([l,r](a[l]==a[r])\),删除这个区间可以得到分数\(\sum_{i=l}^{r}{a[i]}\),问最大得分。
首先我们看到这道题删除区间会涉及到区间和,所以先预处理一个前缀和\(sum[i]\)。
想要最大得分,贪心的想法就是先删除不会影响其他区间的元素,比如区间长度为偶数且每个元素恰好出现两次以及两端元素相等,形如这样的区间\([3,1,2,1,2,3]\)。但是显然这样不好入手,我们还是考虑每个位置可以选择删或者不删,这和01dp很像,考虑动态规划。
所以定义\(dp[i]\)表示前\(i\)个元素能够获得的最大得分;
状态转移:\(dp[i]=\begin{cases}dp[i-1] & 不选择删除a[i],\\dp[j-1]+sum[i]-sum[j-1] &选择删除a[i],a[i]==a[j].\end{cases}\)
那么做法就很明显了:
void solve(){
int n;cin >> n;
vector<int> a(2*n+1),last(n+1,0),sum(2*n+1,0);
for(int i=1;i<=2*n;i++){
cin >> a[i];
}
vector<int> dp(2*n+1,0);
for(int i=1;i<=2*n;i++){
sum[i]=sum[i-1]+a[i];
dp[i]=dp[i-1];
if(last[a[i]]==0){
last[a[i]]=i;
continue;
}
int j=last[a[i]];
int cur=sum[i]-sum[j-1]+dp[j-1];
if(cur>dp[i]) dp[i]=cur;
}
cout << dp[2*n] << endl;
}
但其实比赛的时候没有想到这样做。
F题
知识点:期望dp
\(\hspace{15pt}\)本题为问题的简单版本,两题的唯一区别在于操作失败的代价。
\(\hspace{15pt}\)小红拿到了一个长度为 \(2 \times n\) 的数组 \(\{a_1,a_2,\dots,a_{2\times n}\}\),初始所有元素都是 \(0\),她可以进行任意次以下操作:
\(\hspace{23pt}\bullet\,\)尝试使 \(a_i\) 加 \(1\)。该操作有 \(b_i \%\) 的概率成功。若成功,则 \(a_i\) 加 \(1\);若失败,则无任何变化。。
\(\hspace{15pt}\)小红希望最终 \(a\) 变成一个双排列。她希望最小化操作次数,请你求出小红最优策略下,最终操作次数的期望。答案对 \(10^9+7\) 取模。
这题比较模板,因为这个是一个概率论中的二项分布,而在\(b\%\)的概率下,要成功\(i\)次的期望步数为\(\frac{i}{b\%}\)。有了这个之后加上一点贪心,对于更大的\(i\),我们肯定会选择更大的\(b_i\%\)。所以做法就很显然了:
void solve(){
int n;cin >> n;
vector<int> b(2*n+1);
for(int i=1;i<=2*n;i++){
cin >> b[i];
}
sort(b.begin()+1,b.end());
int ans=0;
for(int i=2*n;i>=1;i--){
int fenzi=100*((i+1)/2);
int inv_fenmu=ksm(b[i],mod-2);
ans=(ans+fenzi*inv_fenmu%mod)%mod;
}
cout << ans << endl;
}
但是也有一个证明:
定义\(dp[i]\)表示从\(i-1\)变为\(i\)的期望步数,假设成功的概率为\(p\),那么转移方程为\(dp[i]=p\times 1+(1-p)\times (dp[i]+1)\),化简得到\(dp[i]=\frac{1}{p}\)。然后每次转移都是独立的,所以从\(0\)变为\(i\)的期望步数为\(\frac{i}{p}\)。
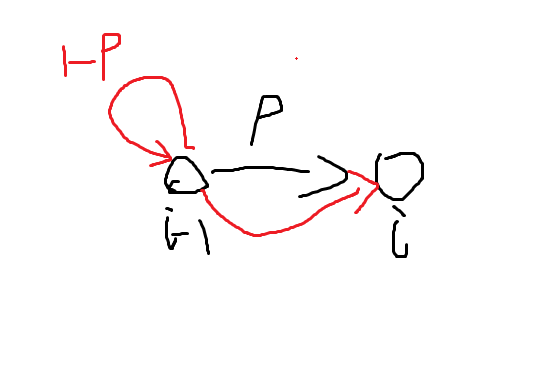
也就是说考虑\(dp[i]\)由\(i-1\)转移过来,那么由两部分组成:成功的话1步期望步数为\(p\times 1\),失败的话有一步消耗到从\(i-1\)到\(i-1\),但是我们\(dp[i]\)的定义是从\(i-1\)转移到\(i\)的期望步数,所以还要加上\(dp[i]\),也就是失败情况下需要走\(1+dp[i]\),也就是红线的部分。
G题
知识点:期望dp,差分
\(\hspace{15pt}\)本题为问题的困难版本,两题的唯一区别在于操作失败的代价。
\(\hspace{15pt}\)小红拿到了一个长度为 \(2 \times n\) 的数组 \(\{a_1,a_2,\dots,a_{2\times n}\}\),初始所有元素都是 \(0\),她可以进行任意次以下操作:
\(\hspace{23pt}\bullet\,\)尝试使 \(a_i\) 加 \(1\)。该操作有 \(b_i \%\) 的概率成功。若成功,则 \(a_i\) 加 \(1\);若失败,如果 \(a_i\) 大于 \(0\) 则会减 \(1\)(等于 \(0\) 则无变化)。
\(\hspace{15pt}\)小红希望最终 \(a\) 变成一个双排列。她希望最小化操作次数,请你求出小红最优策略下,最终操作次数的期望。答案对 \(10^9+7\) 取模。
题意和F不同的就是失败情况下会让\(x-1\),那么还是按照相同的思路定义\(dp[i]\)表示从\(i-1\)转移到\(i\)的期望步数,按照思路,\(dp[i]\)由两部分组成:成功和失败的情况。画出转移图如下:
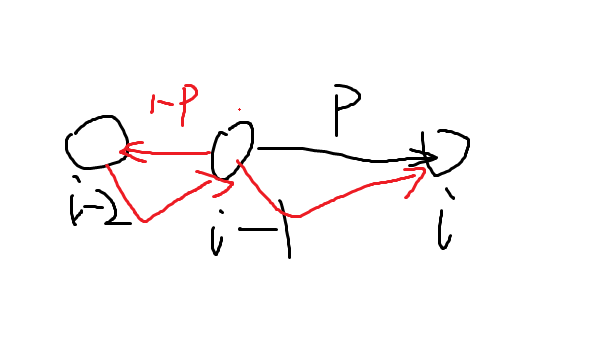
那么\(dp[i]=p\times 1+(1-p)\times (1+dp[i-1]+dp[i])\),后面一部分也就是失败会花费一步从\(i-1\)走到\(i-2\),再花费\(dp[i-1]\)从\(i-2\)走到\(i-1\),再花费\(dp[i]\)从\(i-1\)走到\(i\)。当然这是对于\(i>1\)的情况,对于\(i==1\),也就是F题一样的转移方程,相当于让这题中的\(dp[i-1]=0\),所以我们只需要让\(dp[i-1]=dp[0]=0\)即可。化简得\(dp[i]=\frac{1+dp[i-1]-p\times dp[i-1]}{p}\),这样就得到了从\(i-1\)到\(i\)的期望步数了,但是我们需要的是从\(0\)到\(i\)的期望步数,也就是\(dp[1]+dp[2]+dp[3]+\dots+dp[i]\),这个意思也就是从\(0\)转移到1花费\(dp[1]\),从\(1\)转移到\(2\)花费\(dp[2]\),可以看出直接求出的\(dp\)数组是一个差分数组,因此还要求一个前缀和才是从\(0\)转移到\(i\)的期望步数。
同时可以看到\(b[i]\)的值域为\([1,100]\),所以可以直接预处理每个概率下从\(0\)变为\(n\)的期望步数,这样后面枚举\(b[i]\)的时候直接取答案就可以了。
void solve(){
int n;cin >> n;
vector<vector<int>> dp(105,vector<int>(n+1,0));
int inv=ksm(100,mod-2);//100的逆元
for(int i=1;i<=100;i++){
//枚举概率
int p=i*inv%mod;
int inv_p=ksm(p,mod-2);
for(int j=1;j<=n;j++){
dp[i][j]=(1LL+dp[i][j-1]-p*dp[i][j-1]%mod+mod)%mod*inv_p%mod;
}
for(int j=1;j<=n;j++){
dp[i][j]=(dp[i][j]+dp[i][j-1])%mod;
}
}
vector<int> b(2*n+1);
for(int i=1;i<=2*n;i++){
cin >> b[i];
}
sort(b.begin()+1,b.end());
int ans=0;
for(int i=1;i<=2*n;i++){
ans=(ans+dp[b[i]][(i+1)/2])%mod;
}
cout << ans << endl;
}
时间复杂度为\(O(100\times n)\),是可以接受的。
这场学习最多的就是期望dp。大概掌握了一下如何处理。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号