AtCoder Beginner Contest 409
A题
知识点:枚举
题意为给了两个长度为\(N\)的字符串S1和S2,字符串仅包含o和x字符,问两个字符串是否存在一个位置i使得S1[i]==S2[i]&&S1[i]=='o'。时间复杂度为\(O(n)\)。
void solve(){
int n;cin >> n;
string s1,s2;
cin >> s1 >> s2;
for(int i=0;i<n;i++){
if(s1[i]==s2[i]&&s1[i]=='o'){
cout << "Yes" << endl;
return;
}
}
cout << "No" << endl;
}
B题
知识点:枚举,排序+二分查找
题目陈述
给定一个长度为\(N\)的非负整数序列\(A = (A_1, A_2, \ldots, A_N)\)。找出满足以下条件的最大非负整数\(x\):
- 在\(A\)中,大于或等于\(x\)的元素出现次数(包括重复元素)至少为\(x\)次。
约束条件
- \(1 \leq N \leq 100\)
- \(0 \leq A_i \leq 10^9\)
- 所有输入值均为整数。
解法:由于题目中要找大于等于\(x\)的元素个数,所以可以对序列\(A\)进行升序排序。序列最大长度不超过100,所以我们可以从0到100枚举\(x\),看那一个符合条件即可。可以使用lower_bound()函数获得大于等于\(x\)的元素个数。时间复杂度为\(O(n\times \log{n})\)。
void solve(){
int n;cin >> n;
vector<int> a(n+1);
for(int i=1;i<=n;i++){
cin >> a[i];
}
sort(a.begin()+1,a.end());
int x=0;
for(int i=1;i<=n;i++){
//枚举x
int idx=lower_bound(a.begin()+1,a.end(),i)-a.begin();
if(n-idx+1>=i) x=i;
}
cout << x << endl;
}
C题
知识点:思维,枚举
题目陈述
有一个周长为\(L\)的圆,圆上放置了点\(1, 2, \ldots, N\)。对于\(i = 1, 2, \ldots, N - 1\),点\(i + 1\)位于点\(i\)沿顺时针方向\(d_i\)距离的位置上。
请找出满足以下两个条件的整数三元组\((a, b, c)\)(\(1 \leq a < b < c \leq N\))的数量:
- 点\(a\)、\(b\)、\(c\)都处于不同的位置。
- 以点\(a\)、\(b\)、\(c\)为顶点的三角形是等边三角形。
约束条件
- \(3 \leq L, N \leq 3 \times 10^5\)
- \(0 \leq d_i < L\)
- 所有输入值均为整数。
解法:要出现等边三角形,肯定三个点中任意两个点之间的圆弧长度为\(\frac{L}{3}\),点1的位置为0,每个点在圆周上的位置一定是一个整数,所以如果3不能整除\(L\),那么一定不存在这样的等边三角形,输出为0。否则我们计算每一个点在圆周上的位置,并且用一个\(cnt\)记录每个位置点的数量,之后枚举每一个位置,计算另外两个点的位置,统计答案。这样会有一个问题就是每一个等边三角形会被重复统计,比如枚举到a点时,找到另外两个点b和c,那么枚举到b时,会找到a和c,枚举到c时,会找到a和b,那么就统计了三次,所以最后对答案除以3就是最终的答案了。时间复杂度为\(O(n)\)。
void solve(){
int n,L;cin >> n >> L;
vector<int> d(n);
for(int i=1;i<n;i++) cin >> d[i];
if(L/3*3!=L){
cout << 0 << endl;
return;
}
vector<int> loca(n+1);
int s=0;
loca[1]=s;
for(int i=1;i<n;i++){
s=(s+d[i])%L;
loca[i+1]=s;
}
vector<int> cnt(L,0);
for(int i=1;i<=n;i++){
cnt[loca[i]]++;
}
int ans=0,deg=L/3;
//枚举每一个位置
for(int i=0;i<L;i++){
int p=(i+deg)%L,q=(i+2*deg)%L;
ans+=cnt[i]*cnt[p]*cnt[q];
}
cout << ans/3 << endl;
}
D题
知识点:贪心
问题陈述
给定一个长度为\(N\)、由小写英文字母组成的字符串\(S = S_1S_2\ldots S_N\)。你需要对\(S\)恰好执行一次以下操作:
- 选择\(S\)的一个长度至少为 1 的连续子串,将其循环左移 1 位。也就是说,选择整数\(1 \leq \ell \leq r \leq N\),把\(S_\ell\)插入到\(S\)的第\(r\)个字符右侧,然后删除\(S\)的第\(\ell\)个字符。
找出执行该操作后,所有可能得到的字符串中字典序最小的那个。
你会拿到\(T\)组测试用例,请分别解决每个测试用例。
约束条件
- \(1 \leq T \leq 10^5\)
- \(1 \leq N \leq 10^5\)
- \(S\)是长度为\(N\)、由小写英文字母组成的字符串。
- \(T\)和\(N\)是整数。
- 单个输入文件中所有测试用例的\(N\)之和最多为\(10^5\)。
解法:说到字典序,我们就会想到贪心的思想。在循环左移一次后,要使得字符串字典序是操作后最小的那个,那么肯定是找到第一个\(s_i>s_{i+1}\)的位置\(l\),循环左移后\(s_i=s_{i+1}\)。现在考虑字串的右端点\(r\),要将\(s_l\)移动到后面某个位置,且满足在\(l+2\)到结束的某个位置\(j\)使得\(s_j>s_l\),那么\(r=j-1\)。如果不存在大于\(s_l\)的,那么就把\(s_l\)放在最后。这样一定是最小的,也很容易证明。最后答案就是拼接就好,可以看到上面操作至少包含了3个字符,所以对于\(n \leq 2\)的情况,我们单独处理。时间复杂度为\(O(n)\)。代码写的不是太好。
void solve(){
int n;cin >> n;
string s;cin >> s;
if(n<=2){
if(n==1){
cout << s << endl;
}else{
if(s[0]>s[1]){
reverse(s.begin(),s.end());
}
cout << s << endl;
}
return;
}
string ans;
bool find=false;
for(int i=0;i<n-1;i++){
if(s[i]>s[i+1]){
find=true;
//从i+2去找第一个大于当前字符的
char c=s[i];
ans=s.substr(0,i);
ans+=s[i+1];
int r=n-1,f=0;
for(int j=i+2;j<n;j++){
if(s[j]>c){
r=j;
f=1;
break;
}
}
if(f){
for(int k=i+2;k<=r-1;k++) ans+=s[k];
ans+=c;
for(int k=r;k<n;k++) ans+=s[k];
}else{
for(int k=i+2;k<n;k++) ans+=s[k];
ans+=c;
}
break;
}
}
if(!find) cout << s << endl;
else cout << ans << endl;
}
E题
知识点:树上dp
问题陈述
给定一棵有\(N\)个顶点的树。顶点编号为\(1, 2, \ldots, N\),边编号为\(1, 2, \ldots, N - 1\)。边\(j\)双向连接顶点\(u_j\)和\(v_j\),且权重为\(w_j\)。此外,顶点\(i\)被赋予一个整数\(x_i\)。如果\(x_i > 0\),则在顶点\(i\)放置\(x_i\)个正电子;如果\(x_i < 0\),则在顶点\(i\)放置\(-x_i\)个电子;如果\(x_i = 0\),则顶点\(i\)不放置任何粒子。已知\(\sum_{i=1}^N x_i = 0\)。
沿边\(j\)移动一个正电子或电子需要消耗能量\(w_j\)。当正电子和电子处于同一顶点时,它们会等量相互湮灭。
请找出使所有正电子和电子湮灭所需的最小能量。
约束条件
- \(2 \leq N \leq 10^5\)
- \(|x_i| \leq 10^4\)
- \(\sum_{i=1}^N x_i = 0\)
- \(1 \leq u_j < v_j \leq N\)
- \(0 \leq w_j \leq 10^4\)
- 给定的图是一棵树。
- 所有输入值均为整数。
这道题按照给出的示例模拟一下,可以发现这个就是一道树上dp的题,所以思路也很简单了,定义\(dp[i]\)表示以\(i\)为根的子树将\(i\)的所有孩子向上移动能够获得的代价,由于正负电子相遇会抵消,所以要用一个\(cnt[i]\)来记录每一个节点的的电子情况。之后就是列状态转移方程以及初始化等问题,可以在代码中看到。时间复杂度为\(O(n)\)。
示例:
5
-2 -8 10 -2 2
3 5 1
1 3 5
2 5 0
3 4 6
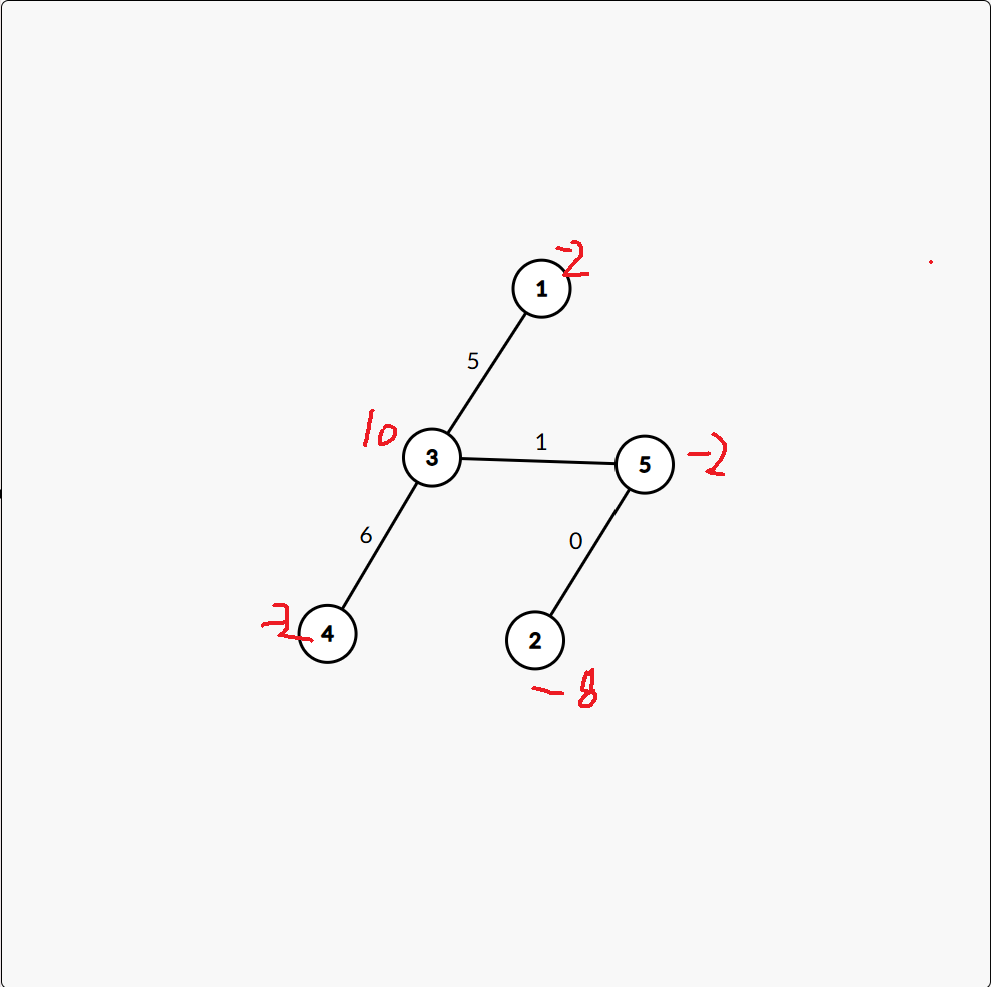
模拟一遍即可。
const int maxn=1e5+9,mod=1e9+7;
//a数组就是每个节点的电子情况,dp[i]表示以i为根的子树的花费,cnt[i]记录节点i的电子情况
int a[maxn],dp[maxn],cnt[maxn];
//tr存树
vector<pair<int,int>> tr[maxn];
void dfs(int u,int p){
//初始化:开始每个节点为dp[u]=0,cnt[u]=a[u]
dp[u]=0;
cnt[u]=a[u];
for(auto[v,w]:tr[u]){
if(v==p) continue;
dfs(v,u);
//注意这里cnt[v]要加绝对值
dp[u]+=dp[v]+w*abs(cnt[v]);
//湮灭电子
cnt[u]+=cnt[v];
}
}
void solve(){
int n;cin >> n;
for(int i=1;i<=n;i++) cin >> a[i];
for(int i=1;i<n;i++){
int u,v,w;
cin >> u >> v >> w;
tr[u].push_back({v,w});
tr[v].push_back({u,w});
}
dfs(1,0);
cout << dp[1] << endl;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号