Seismic Unix 基础使用
目录
基本语法结构
su_command [input] [parameter] [output]
su_command是处理地震数据的核心命令。[input]是输入参数，可以是SU格式的数据文件，也可以是其他命令的输出。[parameter]是可选参数，根据不同命令设置不同处理参数。[output]是指定输出集的名称。
例如使用sfadd命令将两个简单地震数据集相加：
sfadd trace1 = trace1.su trace2 = trace2.su > sum.su
其中，trace1和trace2是输入参数，分别代表两个输入数据集的名称，sum.su是输出结果。
数据格式
SU格式数据包含两类：
- Trace header：包含有关地震道的信息，如采样频率，坐标，时间等。
- Trace data: 实际的地震数据样本序列。
一个SU文件由多个trace组成，每个trace是一个完整的地震数据集，包含从特定检波器获取的连续地震信号。
常见命令中，sfin用来读取trace header信息，sfheader用来修改或显示trace header信息，sfricker用来在trace data中移除地震数据的震相。sfpick 用来在trace data中识别地震数据的初至波。
线性编辑命令与非线性编辑命令
- 线性编辑命令：涉及对地震数据集进行顺序或逆序的组合、切片和增删等操作。SU的线性编辑命令包括
sfadd、sfmul、sfsub等。
sfadd input1 = trace1.su input2 = trace2.su output = sum.su
这个命令将trace1.su和trace2.su这两个数据集的每个trace相加，并将结果存储到sum.su文件中。
- 非线性编辑命令：包括数据筛选、插值和格式转换等，这类操作由sfwindow(时间/空间窗口)、sftransp(数据转置)等命令实现。
例如：使用sfwindow从一个数据集中选取特定时间范围内的数据：
sfwindow window=nt=1000 tr=2.0 dt=0.004 in(trace1.su) out(window_trace.su)
该命令从trace1.su数据集的第二秒开始，选取了1000个样本点，每个样本点的时间间隔是0.004秒，最终生成的window_trace.su数据集就包含了指定时间段的数据。
SU实践经验
Makefile文件
Makefile文件用来对C语言文件进行编译，当项目文件数量过多，手动编译麻烦时，需要手动编写Makefile文件。
使用make命令实现自动化项目构建：
- 检查源文件是否被修改。
- 按顺序编译每个源文件为目标文件
- 将所有目标文件链接为可执行文件
Makefile文件写法：
#!/bin/sh
#shell脚本标识
INC = ${CWPROOT}/include
#定义变量，指向SU库的头文件目录。${CWPROOT}是SU的环境变量，指向SU根目录，/include是SU头文件的标准存放路径。
LIB = ${CWPROOT}/lib
#定义变量，指向SU库的二进制库文件目录，/lib是SU库文件的标准存放路径。
LIK = -lsu -lpar -lcwp -lm
#存储需要链接的库文件参数, 核心库，命令行参数处理库，底层工具库，系统数学库。
main:main.c #编写目标文件与c文件的依赖规则
gcc main.c -o main -I${INC} -L${LIB} ${LIK} #必须用tab缩进，不能是空格，生成目标文件的具体命令。
#-I 指定头文件的搜索路径
#-L${LTB} 指定库文件搜索路径，解决库文件找不到的错误，解决函数未定义的错误。
#${LIK}代入前面定义的库参数。
常用头文件与函数
- par.h : 处理SU程序的命令行参数
- su.h : SU程序核心头文件，定义基础结构和参数
- segy.h : 用于兼容通用地震数据格式
- alloc1float() : SU中安全分配一维浮点数组的工具函数
float *data;
data = alloc1float(5); //定义一个大小为5的一维float数组。记得配一个free1float。
将一个一维浮点数数组中的数据以二进制格式写入名为sin.bin的文件中。
FILE *fp; //定义文件指针
fp = fopen("sin.bin", "wb+"); //对文件以写入方式，以二进制模式打开，若文件不存在则创建，若存在则清空原有内容
for(int i = 0; i < nt; i++) //以二进制循环写入数据
{
fwrite(&data[i], sizeof(float), 1, fp);//第一个参数是指针，第二个参数是单个数据字节大小，第三个数据是每次写入数据个数，第四个参数是目标文件指针。
}
fclose(fp); //关闭文件
安全写法：
FILE *fp;
if((fp = fopen("sin.bin", "wb+")) == NULL){
printf("Can not open \"sin.bin\"");
exit(0);
}else{
fp = fopen("sin.bin", "wb+");
for(int i = 0; i < nt; i++)
{
fwrite(&data[i], nt*sizeof(float), 1, fp);
}
}
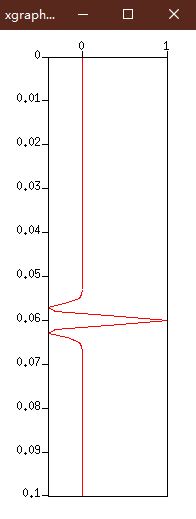
xgraph命令
xgraph n1= [optional parameters] <binaryfile
Required Parameters:
- n1 array containing number of points per plot
Optional Parameters:
- d1=0.0,... x sampling intervals
- d2=0.0,... y sampling intervals
地震信号的正弦函数思路
实际编程中：
\[\sum_{i = 0}^{n}i·dt·1.0 = t
\]
#include <stdio.h>
#include <su.h>
#include <math.h>
#include <par.h>
#include <segy.h>
int main()
{
int nt = 101;
float *data = alloc1float(nt);
float dt = 0.01, fm = 10.0;
for(int i = 0; i < nt; i++)
{
data[i] = sin(i * 1.0 * dt * fm * PI * 2);
}
FILE *fp;
if((fp = fopen("sin.bin", "wb+")) == NULL)
{
printf("Can not open \"sin.bin\". \n");
exit(0);
}else{
fp = fopen("sin.bin", "wb+");
for(int i = 0; i < nt; i++)
{
fwrite(&data[i], sizeof(float), 1, fp);
}
}
free1float(data);
return 0;
}
Ximage命令
ximage n1= [optional parameters] <binaryfile
n1: number of samples in 1st (fast) dimension
d1=1.0: sampling interval in 1st dimension
ximage n1=301 n2=401 d1=1 <velocity.bin \\两层水平介质均匀模型
ximage是地震数据处理中常用的工具，其核心功能是将二进制浮点数据解析为灰度图像，数据中每一个浮点值，一个像素的灰度值。
正演模拟速度模型
#include <stdio.h>
#include <su.h>
#include <par.h>
#include <segy.h>
#include <math.h>
int nz = 301, nx = 401;
float *data;
void Alloc()
{
data = alloc1float(nx * nz);
memset(data, 0, nx * nz * sizeof(float));
}
void Free()
{
free1float(data);
}
void Output_2d_bin(char *filename, float *data, int nx, int nz)
{
FILE *fp;
if((fp = fopen(filename, "wb+")) == NULL){
printf("Cannot open %s\n", filename);
exit(0);
}else{
fp = fopen(filename, "wb+");
for(int ix = 0; ix < nx; ix++)
{
for(int iz = 0; iz < nz; iz++){
fwrite(&data[iz * nx + ix], sizeof(float), 1, fp);
}
}
fclose(fp);
}
}
void Generate_veloc(float *data, int nx, int nz)
{
for(int iz = 0; iz < nz; iz++)
{
for(int ix = 0; ix < nx; ix++){
if(iz <= 150){
data[iz * nx + ix] = 2000;
}else if(iz > 150 && iz <= 200){
data[iz * nx + ix] = 2500;
}else{
data[iz * nx + ix] = 3000;
}
}
}
}
int main()
{
Alloc();
Generate_veloc(data, nx, nz);
Output_2d_bin("velocity.bin", data, nx, nz);
Free();
return 0;
}
命令行：
ximage n1=301 <velocity.bin
制作雷克子波
#include <stdio.h>
#include <su.h>
#include <segy.h>
#include <math.h>
#include <par.h>
int nt = 101;
float dt = 0.005, *wavelet, fm = 30.0;
void Alloc();
void Gen_Wave(float *wavelet, int nt);
void Output(char *filename, float *wavelet, int nt);
void Free();
int main()
{
Alloc();
Gen_Wave(wavelet, nt);
Output("wavelet.bin", wavelet, nt);
Free();
return 0;
}
void Alloc()
{
wavelet = alloc1float(nt);
}
void Free()
{
free1float(wavelet);
}
void Gen_Wave(float *wavelet, int nt)
{
for(int it = 0; it < nt; it++)
{
float t = it * 1.0 * dt - 0.3; \\雷克子波时移
float temp = PI * fm * t;
wavelet[it] = (1.0 - 2.0 * temp * temp) * exp(-temp * temp);
}
}
void Output(char *filename, float *wavelet, int nt)
{
FILE *fp;
if((fp = fopen(filename, "wb+")) == NULL){
printf("Can not open %s", filename);
exit(0);
}else{
fp = fopen(filename, "wb+");
fwrite(wavelet, nt * sizeof(float), 1, fp);
fclose(fp);
}
}
一维数组表达多维数组
可以用一维数组表达多维数组，为后续GPU加速做准备。
一维数组的初始化：
memset(data, 0, nsize * sizeof(float));
- 行优先存储：nz列数，nx行数
for(int iz = 0; iz < nz; iz++)
{
for(int ix = 0; ix < nx; ix++)
{
b[iz * nx + ix] = b[iz][ix];
}
}
- 列优先存储：nz列数，nx行数
for(int iz = 0; iz < nz; iz++)
{
for(int ix = 0; ix < nx; ix++)
{
b[ix * nz + iz] = b[iz][ix];
}
}
- 三维数组一维表达：
data[iy * nx * nz + iz * nx + ix] = data[iy][iz][ix];
正演模拟
正演模拟就是波场模拟，在已知地下构造的情况下，通过正演得到一套地震地震数据，然后假装不知道地下构造，用正演出来的地震数据结合成像方法得到一个地下构造，通过对比成像效果，来判断成像技术是否足够好。
- 速度场设计：
正演模拟的第一步首先是设计速度场，层状构造速度模型本质是一个二维数组，两个维度来表示横纵坐标距离，数值中每个值是它的速度，此外还要定义网格间距dx, dz，即每个网格是多少米。为了高阶有限差分的稳定性，dx, dz通常设定为5或10。 - 制作地震子波：
正演模拟的第二步是设计地震子波，通常是用雷克子波。
雷克子波时移：雷克子波时移是正演模拟时，指雷克子波在时间轴上平移，即改变子波的起始时间和峰值位置，使其在时间维度上整体向前或向后移动。
\[w(t) = (1-2π^2f_0^2t^2)e^{-π^2f_0^2t^2}
\]
其中t为时间变量；f_0为子波的主频，决定子波的宽窄，主频越高，子波越窄。
时移操作本质是对时间变量t进行替换，时移后的雷克子波表达式：
\[w(t-φ) = (1-2π^2f_0^2(t-φ)^2)e^{-π^2f_0^2(t-φ)^2}
\]
左加右减。
时移不改变子波的主频、波形形状和能量，仅改变其在时间轴上的位置。
制作地震子波，即将地震子波作为震源相，相当于作为一块石子扔到水里面，要让雷克子波震源的这个震动状态传递给地震波场。
- 实现声波波场方程：
2D声波波动方程：
\[\frac{1}{v^2(x,z)} \frac{∂^2P(x, z, t)}{∂t^2} = \frac{∂^2P(x, z, t)}{∂x^2} + \frac{∂^2P(x, y, z)}{∂z^2}
\]
3D声波波动方程：
\[\frac{1}{v^2(x, y, z)} \frac{∂^2P(x, y, z, t)}{∂t^2} = \frac{∂^2P(x, y, z, t)}{∂x^2} + \frac{∂^2P(x, y, z, t)}{∂y^2} + \frac{∂^2P(x, y, z, t)}{∂z^2}
\]
为了在代码中实现偏导，通常采用有限差分法：通过引入更多的数据点参与计算。
偶数阶高阶有限差分：差分阶数=参与的数据点数（不算中间点）。
参考文献：刘洋，李承楚. 任意偶数阶精度有限有限差分法数值模拟[J].石油地球物理勘探，1998，33(1):1-10.
高精度波场数值模拟：采用高阶有限差分法离散声波波动方程进行波长数值模拟
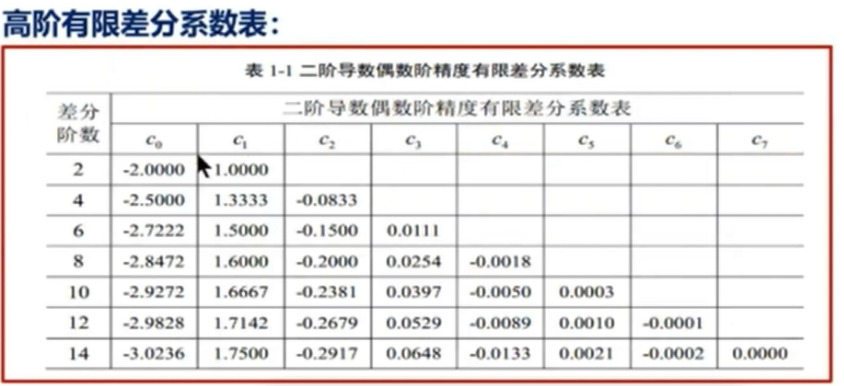
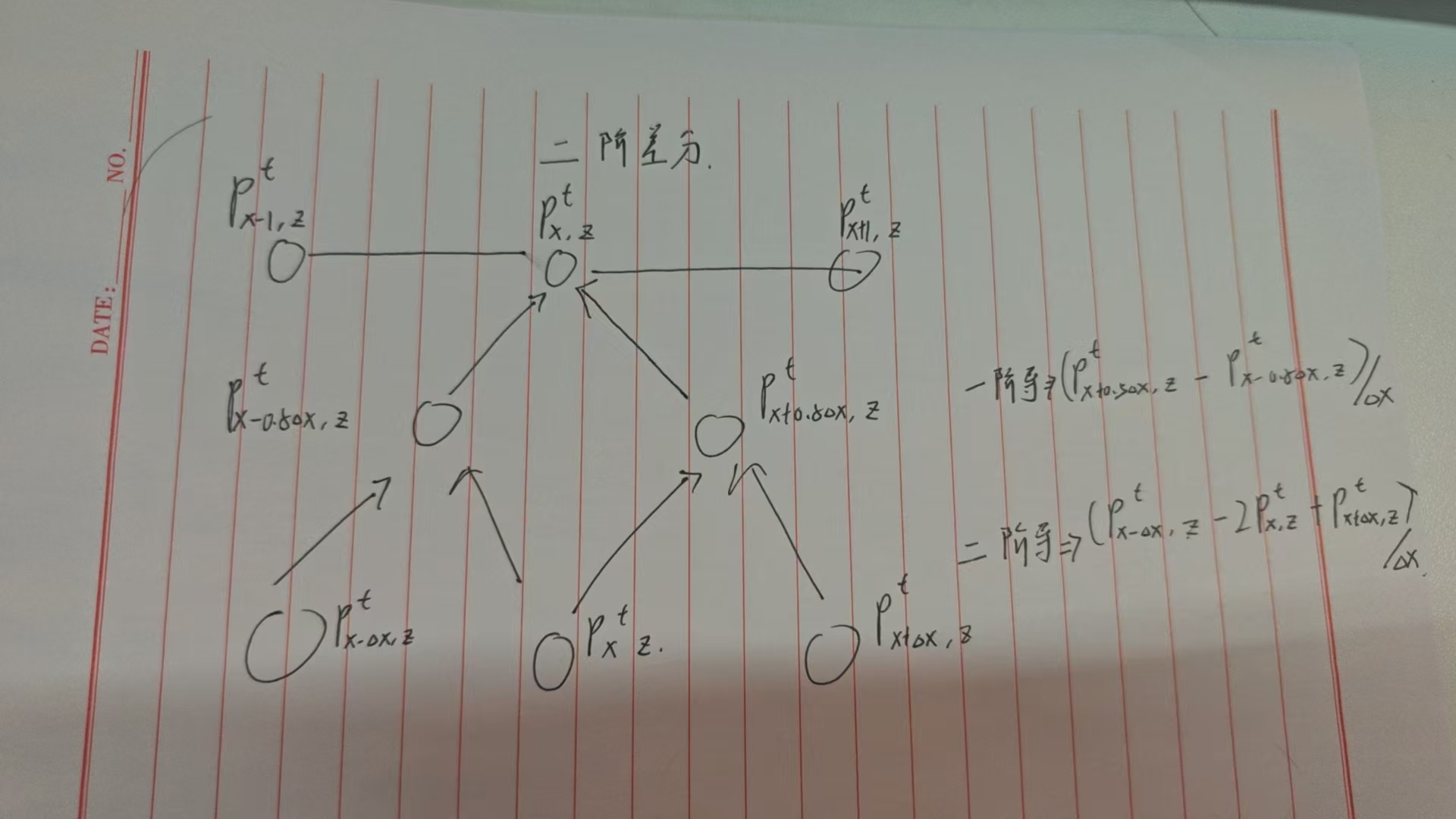
- 正演模拟具体实现代码：
lib.c
void output_1d_bin(char * filename, float *data, int nx)
{
FILE *fp;
if((fp = fopen(filename, "wb+")) == NULL)
{
printf("Can not open this bin\n");
exit(0);
}else{
fwrite(data, nx * sizeof(float), 1, fp);
}
fclose(fp);
}
void output_2d_bin(char * filename, float *data, int nx, int nz)
{
FILE *fp;
if((fp = fopen(filename, "wb+")) == NULL){
printf("Can not open this bin \n");
exit(0);
}else{
fwrite(data, nx * nz * sizeof(float), 1, fp);
}
fclose(fp);
}
void generate_wavelet(float *data, int nt, float fm, float dt)
{
float temp;
int itshift;
for(int it = 0; it < nt; it++){
itshift = it - (int)(1.0/fm/dt);
temp = PI * PI * fm * fm * (itshift * 1.0) * dt * (itshift * 1.0) * dt;
data[it] = (1.0 - 2.0 * temp) * exp(-1.0 * temp);
}
}
void add_wavelet(float *wf, float *wavelet, int nx, int nz, int it, int sx, int sz)
{
wf[sx * nz + sz] = wf[sx * nz + sz] + wavelet[it];
}
void generate_coe(float *coe)
{
coe[0] = -2.0;
coe[1] = 1.0;
}
void extrapolation(float *wf1, float *wf2, float *velocity, int nx, int nz, float dx, float dz, float dt, float*coe, int N)\\更高阶的有限差分主要更改这个代码
{
for(int ix = N / 2; ix < nx - N / 2; ix++)
{
for(int iz = N / 2; iz < nz - N / 2; iz++)
{
wf1[ix * nz + iz] = 2.0 * wf2[ix * nz + iz] - wf1[ix * nz + iz] + velocity[ix * nz + iz] * velocity[ix * nz + iz] * dt * dt / dz / dz *
(coe[1] * wf2[ix * nz + iz - 1] + coe[0] * wf2[ix * nz + iz] + coe[1] * wf2[ix*nz + iz + 1])
+ velocity[ix * nz + iz] * velocity[ix * nz + iz] * dt * dt / dx / dx *
(coe[1] * wf2[(ix-1) * nz + iz] + coe[0] * wf2[ix * nz + iz] + coe[1] * wf2[(ix + 1)*nz + iz]);
}
}
}
void generate_velocity(float *data23, int nx, int nz)
{
for(int ix = 0; ix < nx; ix++){
for(int iz = 0; iz < nz; iz++)
{
if(iz <= 150){
data23[ix * nz + iz] = 2500.0;
}else{
data23[ix * nz + iz] = 3000.0;
}
}
}
}
void replace_wf(float *wf1, float *wf2, int nx, int nz)
{
float temp;
for(int ix = 0; ix < nx; ix++)
{
for(int iz = 0; iz < nz; iz++)
{
temp = wf1[ix * nz + iz];
wf1[ix * nz + iz] = wf2[ix * nz + iz];
wf2[ix * nz + iz] = temp;
}
}
}
void Alloc(){
wavelet = alloc1float(nt);
memset(wavelet, 0, nt * sizeof(float));
velocity = alloc1float(nx * nz);
memset(velocity, 0, nx * nz * sizeof(float));
wf1 = alloc1float(nx * nz);
memset(wf1, 0, nx * nz * sizeof(float));
wf2 = alloc1float(nx * nz);
memset(wf2, 0, nx * nz * sizeof(float));
coe = alloc1float(N/2 + 1);
memset(coe, 0, (N / 2 + 1) * sizeof(float));
}
void Free(){
free1float(velocity);
free1float(wavelet);
free1float(wf1);
free1float(wf2);
free1float(coe);
}
main.c
#include <stdio.h>
#include <par.h>
#include <su.h>
#include <segy.h>
#include <math.h>
int nx = 401, nz = 301, nt = 501, sx = 200, sz = 100, N = 2;
float dx = 5.0, dz = 5.0, dt = 0.001, fm = 30.0;
float *velocity, *wavelet, *wf1, *wf2, *coe;
#include "lib.c"
int main()
{
Alloc();
generate_wavelet(wavelet, nt, fm, dt);
output_1d_bin("ricker.bin", wavelet, nt);
generate_velocity(velocity, nx, nz);
output_2d_bin("velocity.bin", velocity, nx, nz);
generate_coe(coe);
for(int it = 0; it < nt; it++)
{
add_wavelet(wf2, wavelet, nx, nz, it, sx, sz);//添加子波
extrapolation(wf1, wf2, velocity, nx, nz, dx, dz, dt, coe, N);//波场方程
replace_wf(wf1, wf2, nx, nz);//
//wf1 = wf2;
//wf2 = wf3;
if(it == 200){
output_2d_bin("wf.bin", wf2, nx, nz);//这里放时间
}
}
Free();
return 0;
}
实现效果：
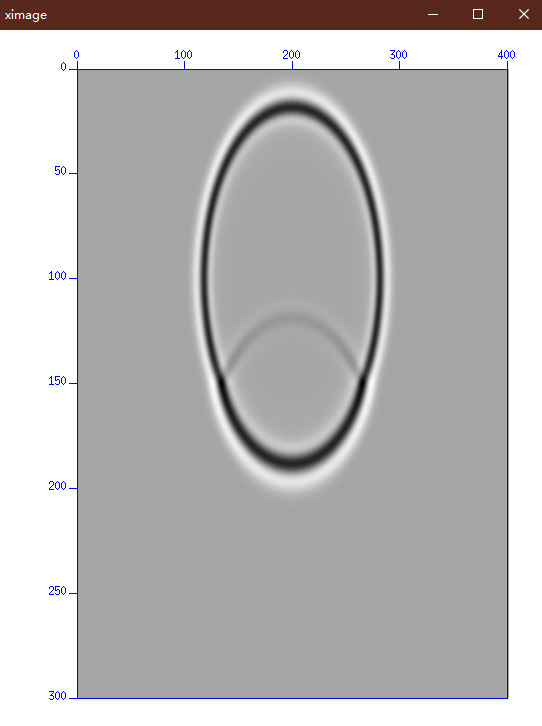
后续改进：
- 思考如何实现高阶差分，使得二阶导更加精确。
- 如何按行优先来设计整个正演模拟。
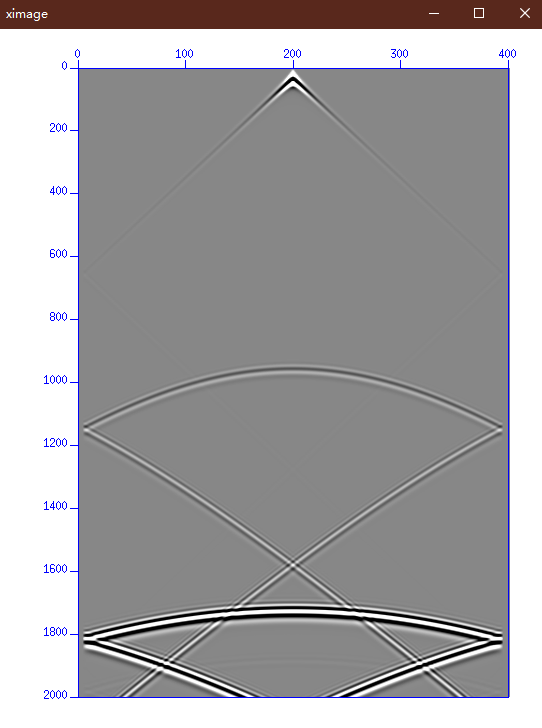
- 正演模拟制作共炮点时距曲线
//main.c
#include <stdio.h>
#include <par.h>
#include <su.h>
#include <segy.h>
#include <math.h>
int nx = 401, nz = 301, nt = 2001, sx = 200, sz = 5, N = 10;//sx sz 炮点, 一般认为sz等于5就算是地表。
float dx = 8.0, dz = 8.0, dt = 0.001, fm = 30.0;
float *velocity, *wavelet, *wf1, *wf2, *coe, *data;
#include "lib.c"
int main()
{
Alloc();
generate_wavelet(wavelet, nt, fm, dt);
output_1d_bin("ricker.bin", wavelet, nt);
generate_velocity(velocity, nx, nz);
output_2d_bin("velocity.bin", velocity, nx, nz);
generate_coe(coe);
for(int it = 0; it < nt; it++)
{
add_wavelet(wf2, wavelet, nx, nz, it, sx, sz);//添加子波
extrapolation(wf1, wf2, velocity, nx, nz, dx, dz, dt, coe, N);//波场方程
replace_wf(wf1, wf2, nx, nz);
if(it == 300){
output_2d_bin("wf.bin", wf2, nx, nz);//这里放时间
}
copydata(data, wf2, nx, it, nt, nz);
}
fileout("csp.bin", data, nt, nx);
Free();
return 0;
}
//lib.c
void output_1d_bin(char * filename, float *data, int nx)
{
FILE *fp;
if((fp = fopen(filename, "wb+")) == NULL)
{
printf("Can not open this bin\n");
exit(0);
}else{
fwrite(data, nx * sizeof(float), 1, fp);
}
fclose(fp);
}
void fileout(char * filename, float *data, int nx, int nt)
{
FILE * fp;
if((fp = fopen(filename, "wb+")) == NULL){
printf("Can not open this bin \n");
exit(0);
}else{
fwrite(data, nx * nt * sizeof(float), 1, fp);
}
fclose(fp);
}
void output_2d_bin(char * filename, float *data, int nx, int nz)
{
FILE *fp;
if((fp = fopen(filename, "wb+")) == NULL){
printf("Can not open this bin \n");
exit(0);
}else{
fwrite(data, nx * nz * sizeof(float), 1, fp);
}
fclose(fp);
}
void generate_wavelet(float *data, int nt, float fm, float dt)
{
float temp;
int itshift;
for(int it = 0; it < nt; it++){
itshift = it - (int)(1.0/fm/dt);
temp = PI * PI * fm * fm * (itshift * 1.0) * dt * (itshift * 1.0) * dt;
data[it] = (1.0 - 2.0 * temp) * exp(-1.0 * temp);
}
}
void add_wavelet(float *wf, float *wavelet, int nx, int nz, int it, int sx, int sz)
{
wf[sx * nz + sz] = wf[sx * nz + sz] + wavelet[it];
}
void generate_coe(float *coe)
{
coe[0] = -2.9272;
coe[1] = 1.6667;
coe[2] =-0.2381;
coe[3] = 0.0397;
coe[4] =-0.0050;
coe[5] =0.0003;
}
void extrapolation(float *wf1, float *wf2, float *velocity, int nx, int nz, float dx, float dz, float dt, float*coe, int N)
{
for(int ix = N / 2; ix < nx - N / 2; ix++)
{
for(int iz = N / 2; iz < nz - N / 2; iz++)
{
wf1[ix * nz + iz] = 2.0 * wf2[ix * nz + iz] - wf1[ix * nz + iz]
+ velocity[ix * nz + iz] * velocity[ix * nz + iz] * dt * dt / dz / dz *
(coe[1] * wf2[ix * nz + iz - 1] + coe[0] * wf2[ix * nz + iz] + coe[1] * wf2[ix*nz + iz + 1]
+ coe[2] * (wf2[ix * nz + iz - 2] + wf2[ix * nz + iz + 2]) + coe[3] * (wf2[ix * nz + iz - 3] + wf2[ix * nz + iz + 3]) + coe[4]
*(wf2[ix * nz + iz - 4] + wf2[ix * nz + iz + 4]) + coe[5] *(wf2[ix * nz + iz - 5] + wf2[ix * nz + iz + 5]))
+ velocity[ix * nz + iz] * velocity[ix * nz + iz] * dt * dt / dx / dx *
(coe[1] * wf2[(ix-1) * nz + iz] + coe[0] * wf2[ix * nz + iz] + coe[1] * wf2[(ix + 1)*nz + iz] + coe[2] * (wf2[(ix - 2) * nz + iz] +
wf2[(ix + 2) * nz + iz] )+coe[3] * (wf2[(ix - 3) * nz + iz] + wf2[(ix + 3) * nz + iz]) + coe[4] * (wf2[(ix - 4) * nz + iz] + wf2[(ix+4
) * nz + iz]) + coe[5] * (wf2[(ix - 5) * nz + iz] + wf2[(ix + 5) * nz + iz]));
}
}
}
void generate_velocity(float *data23, int nx, int nz)
{
for(int ix = 0; ix < nx; ix++){
for(int iz = 0; iz < nz; iz++)
{
if(iz <= 150){
data23[ix * nz + iz] = 2500.0;
}else{
data23[ix * nz + iz] = 3000.0;
}
}
}
}
void replace_wf(float *wf1, float *wf2, int nx, int nz)
{
float temp;
for(int ix = 0; ix < nx; ix++)
{
for(int iz = 0; iz < nz; iz++)
{
temp = wf1[ix * nz + iz];
wf1[ix * nz + iz] = wf2[ix * nz + iz];
wf2[ix * nz + iz] = temp;
}
}
}
void Alloc(){
wavelet = alloc1float(nt);
memset(wavelet, 0, nt * sizeof(float));
velocity = alloc1float(nx * nz);
memset(velocity, 0, nx * nz * sizeof(float));
wf1 = alloc1float(nx * nz);
memset(wf1, 0, nx * nz * sizeof(float));
wf2 = alloc1float(nx * nz);
memset(wf2, 0, nx * nz * sizeof(float));
coe = alloc1float(N/2 + 1);
memset(coe, 0, (N / 2 + 1) * sizeof(float));
data = alloc1float(nx * nt);
memset(data, 0, nx * nt * sizeof(float));
}
void copydata(float *data, float *wf, int nx, int it, int nt, int nz)
{
int iz = N / 2;
for(int ix = 0; ix < nx; ix++)
{
data[ix * nt + it] = wf[ix * nz + iz];
}
}
void Free(){
free1float(velocity);
free1float(wavelet);
free1float(wf1);
free1float(wf2);
free1float(coe);
free1float(data);
}
//命令行：
ximage n1=2001 perc=99 <csp.bin
在 Linux 的 Vim 中粘贴代码时出现缩进错乱:（临时好用方法）
- 在普通模式下输入
:set paste, 进入--INSERT(paste)--模式。 - 粘贴完成后输入
:set nopaste, 退出该模式。
浙公网安备 33010602011771号