算法设计与分析实验
贪心算法
贪心算法总是做出在当前看来事最好的选择。也就是说,贪心算法并不从整体最优上加以考虑,所做的选择只是在某种意义上的局部最优选择。
注:贪心算法不是对所有问题都能得到整体最优解,但对许多问题产生整体最优解,比如最小生成树问题、图的单源最短路径问题等
贪心算法和动态规划的差异
动态规划算法中,每步所做的选择往往依赖于相关子问题的解。因而只有解出相关子问题后,才嫩做出选择。
贪心算法中,仅在当前状态下做出最好的选择,即局部最优选择。再去解做出这个选择后产生的相应的子问题。贪心算法所做的贪心选择可以依赖以往所做过的选择,但决不依赖将来所作的选择,也不依赖子问题的解。
正式上述差别,动态规划算法通常以自底向上的方式解各子问题,贪心算法则通常以自顶向下的方式进行。
具体的差异,通过经典的背包问题阐述,看问题2.
1. 活动安排问题
设有n个活动的集合E={1,2,....,n},其中每个活动都要求使用同一资源,如演讲场会等,而在同一时间内只有一个活动能使用这一资源。每个活动i都有要求使用该资源的起始时间\(s_{i}\)和结束时间\(f_{i}\),且\(s_{i}<f_{i}\)。
活动i和活动j相容=时间错开=当\(s_{i}\ge f_{j}或s_{j}\ge f_{j}\)时
活动安排问题,就要要在所给的活动集合中选出最大的相容活动子集合。
//先对活动按结束时间飞递减排序
void GreedySelector(int n,Type s[],Type f[],bool A[])
{
A[1]=true;
int j=1;
for(int i=2;i<=n;i++)
{
if(s[i]>=f[j])//检查之后的活动与A中活动的相容性。
{//相容,则纳入A中
A[i]=true;
j=i;
}
else//不相容,则不纳入
A[i]=false;
}
}
算法示例:
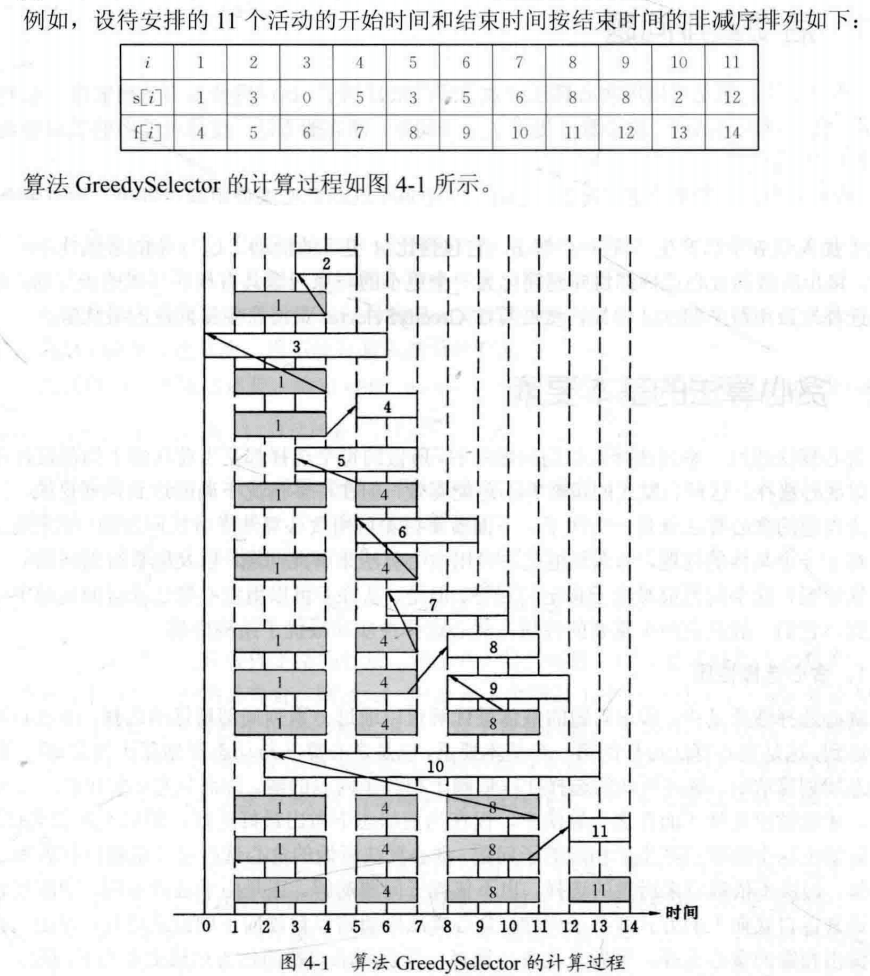
选择贪心算法的意义:使剩余的可安排时间段极大化,以便安排尽可能多的相容活动。
具体实践代码:
#include<iostream>
#define max 101
using namespace std;
/*
11
1 4
3 5
0 6
5 7
3 8
5 9
6 10
8 11
8 12
2 13
12 14
*/
int n;
float s[max],f[max];
bool A[max];
struct T
{
float s;
float f;
};
T* t;
void swap(T* t1,T*t2)
{
T temp=*t1;
*t1=*t2;
*t2=temp;
}
void sorted(T* t,int n)
{
for(int i=0;i<n-1;i++)
for(int j=0;j<n-i-1;j++)
{
if(t[j].f>t[j+1].f)
swap(t[j],t[j+1]);
}
}
void GreedySelector(int n,T* t,bool A[max])
{
A[0]=true;
int j=0;
for(int i=1;i<n;i++)
{
if(t[i].s>=t[j].f)
{
A[i]=true;
j=i;
}
else
A[i]=false;
}
}
int main()
{ t=new T[max];
cin>>n;
for(int i=0;i<n;i++)
{
cin>>t[i].s>>t[i].f;
A[i]=false;
}
sorted(t,n);
cout<<"排序后:"<<endl;
for(int j=0;j<n;j++)
cout<<t[j].s<<" "<<t[j].f<<endl;
GreedySelector(n,t,A);
for(int j=0;j<n;j++)
{
if(A[j])
cout<<"活动:"<<j+1;
}
return 0;
}
2 背包问题与01背包问题
0-1背包问题:给定n种物品和一个背包。物品i的重量是\(w_{i}\),其价值为\(v_{i}\),背包的容量为c。问应如何选择装入背包中的物品,使得装入背包中物品的总价值最大?
在选择装入背包的物品时,对每种物品i只有两种选择,即装入背包或不装入背包。不能将物品i装入背包多次,也能只装入部分的物品i。
形式化表述:\(给定c>0,w_{i}>0,v_{i}>0 (1\leq i\leq n),要求找出一个n元的0-1向量(x_{1},x_{2},...,x_{n}),x_{i}\in \{0,1\},1\leq i\leq n,使得\sum_{i=1}^n w_{i}x_{i}\leq c,而且\sum_{i=1}^n v_{i}x_{i}达到最大\)
背包问题:与0-1背包问题相似,不同的是在选择物品\(i(1\leq i\leq n)\)装入背包式,可以选择物品i的一部分,而不一定要全部装入背包。
形式化表述:\(给定c>0,w_{i}>0,v_{i}>0 (1\leq i\leq n),要求找出一个n元向量(x_{1},x_{2},...,x_{n}),x_{i}\in \{0,1\},0\leq x_{i}\leq 1,1\leq i\leq n,使得\sum_{i=1}^n w_{i}x_{i}\leq c,而且\sum_{i=1}^n v_{i}x_{i}达到最大\)
背包问题可以用贪心算法求解,但0-1背包问题不能用贪心算法求解。
背包问题的贪心算法描述
void Knapsack(int n,float M,float v[],float w[],float x[])
{
Sort(n,v,w);//按单位重量价值降序排列
int i;
for(i=1;i<=n;i++)
x[i]=0;
float c=M;//c为背包容量
for(i=1;i<=n;i++) //如果当前物品重量小于背包容量,则将物品装入,更新背包容量为除去当前物品的重量。
{
if(w[i]>c)
break;
x[i]=1;
c-=w[i];
}
if(i<=n) //当物品没装满,统计背包容量能还能装多少。
x[i]=c/w[i];
}

3. 背包问题:
算法思想:
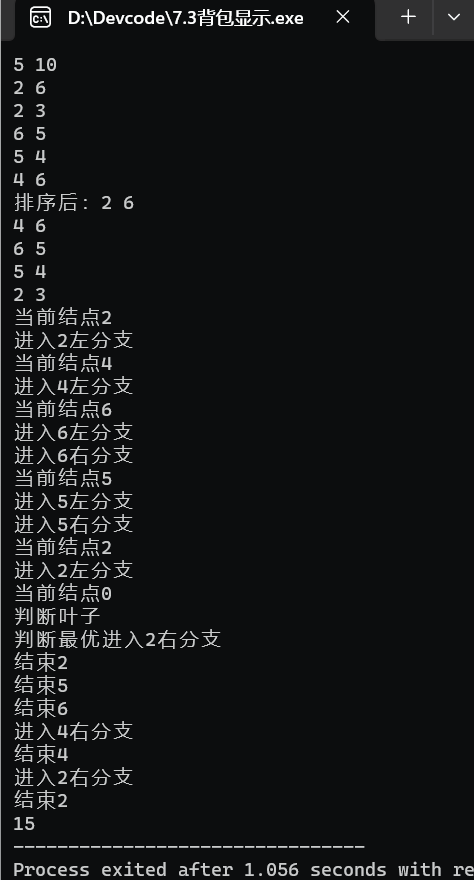
基于贪心算法的背包问题是可以得到最优解的。其算法思想是先按单位价值对物品进行排序,优先选择单位价值最高的物品进行装入,直至背包容量满载。
执行结果:
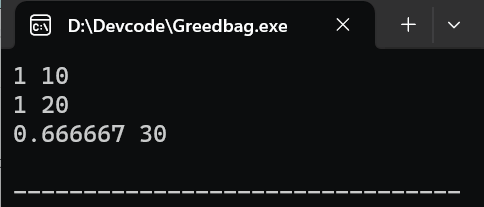
实现代码:
#include <iostream>
#define Max 20
using namespace std;
struct T
{
float v;
float w;
float pval;
};
T* t;
int n;
float W;
float x[Max];
void swap(T* t1,T* t2)
{
T temp=*t1;
*t1=*t2;
*t2=temp;
}
void Sort()
{
for(int i=0;i<n-1;i++)
for(int j=0;j<n-i-1;j++)
{
if(t[i].pval<t[i+1].pval)
{
swap(t[i],t[i+1]);
}
}
}
void knapsack()
{
Sort();
int i;
for(i=0;i<n;i++)
{
x[i]=0;
}
float c=W;
for(i=0;i<n;i++)
{
if(t[i].w>c)
break;
x[i]=1;
c=c-t[i].w;
}
if(i<=n)
x[i]=c/t[i].w;
}
void output()
{
for(int i=0;i<n;i++)
{
cout<<t[i].v<<endl;
cout<<t[i].w<<endl;
cout<<t[i].pval<<endl;
}
}
int main()
{
t=new T[Max];
n=3;
//初始化物品权重和价值
W=50;
t[0].v=60;
t[0].w=10;
t[0].pval=t[0].v/t[0].w;
t[1].v=100;
t[1].w=20;
t[1].pval=t[1].v/t[1].w;
t[2].v=120;
t[2].w=30;
t[2].pval=t[2].v/t[2].w;
// output();
// Sort();
// cout<<"Sorted:"<<endl;
// output();
knapsack();
for(int i=0;i<n;i++)
cout<<x[i]<<" "<<t[i].w<<endl;
}
回溯法
1.子集和问题
问题:

参考:
具体分析:
#include<iostream>
using namespace std;
#define max 1000
int n,c; //元素数,目标和
int csum,r;//当前和,剩余和
int x[max]={0};//元素数组
int w[max];//s数值数组
bool backtrack(int i)
{
//终止:到叶节点
if(i>=n)
{
if(csum==c) return true;
else return false;
}
r-=w[i];//除去i后的剩余和
//约束左分支:当前和大于目标和,左分支可剪
if(csum+w[i]<=c)
{
x[i]=1;
csum+=w[i];
//判断左分支是否有解
if(backtrack(i+1))
return true;
//else return false; 这地方写false就不进入右分支了
csum-=w[i];
}
//约束右分支:当前和加剩余和(不包括w[i])是否大于目标和,
//是,则分支;不是,则剪枝(因为没意义)
if(csum+r>=c)
{
x[i]=0;
if(backtrack(i+1))
return true;
}
r+=w[i];
return false;
}
int main(){
cin>>n>>c;
int i;
for(i=0;i<n;i++){
cin>>w[i];
r+=w[i];
}
if(backtrack(0))
{
int j;
for(j=0;j<n;j++)
if(x[j]==1)
cout<<w[j]<<" ";
}
else
cout<<"No Solution!"<<endl;
return 0;
}
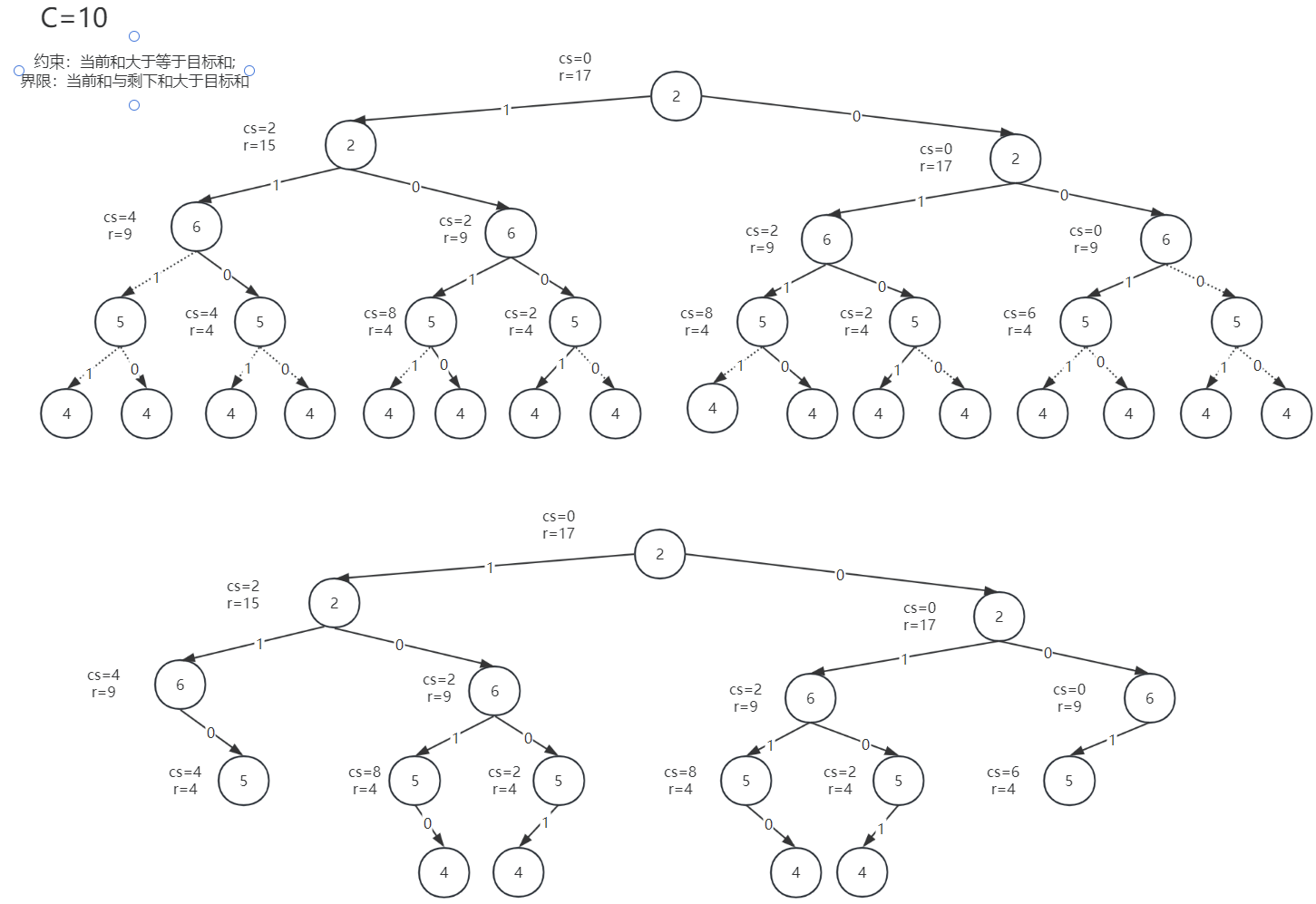
问题:
- r(剩余和)在进入左右分支前后要更新和回复。(模板之一)
- 这是有返回的backtrack,所以跟无返回的有点差别,差别在返回,无返回的遇到某个解后会继续往后探索;
- 还有return false问题,左分支内你想写return false,那你右分支不进行了?。
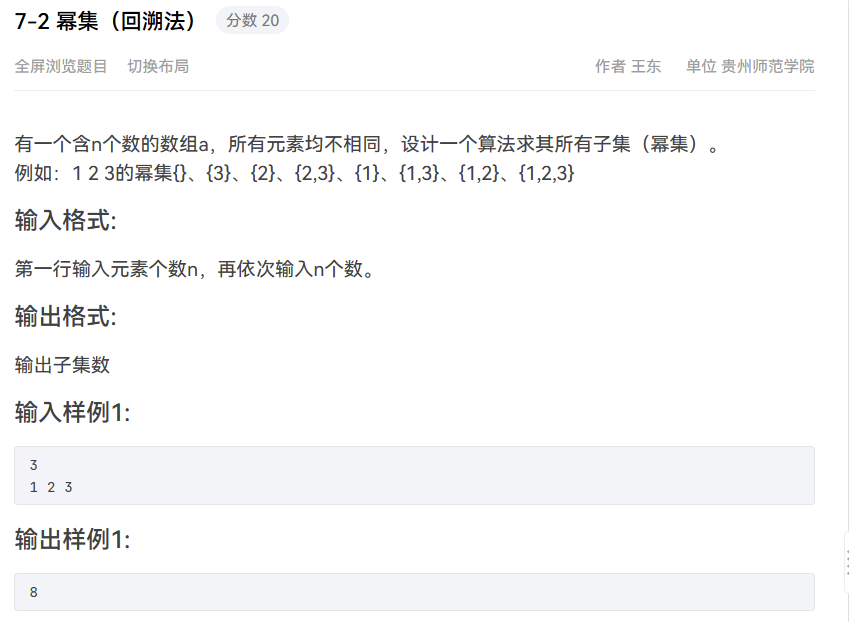
2.幂集问题
问题:
———————————————————————————————————————————
参考:
具体分析:
#include<iostream>
using namespace std;
#define Max 255
int n;//元素个数
int w[Max];
int x[Max];//元素数组
int count=0;//子集个数
void backtrack(int i)
{
//终止
if(i>n)
{
count++;//!!或者加return;就不用写else
}else{//!!这里的else加了,当到叶节点就不往后执行了。
w[i]=1;
backtrack(i+1);
w[i]=0;
backtrack(i+1);
}
}
int main()
{
int i;
cin>>n;
for(i=0;i<n;i++)//输入元素
{
cin>>x[i];
}
backtrack(1);//为什么从1开始,画个图就知道了
cout<<count<<endl;
return 0;
}
问题:
- 想着套子集和的框架,这个只需遍历所有结果就行。不用考虑剪枝。
- 返回的问题(是否用else)
不加else,到叶节点了,也会继续递归,会造成错误。
要么加else,终止了就不执行else代码块;要么不加else,但if里加return;
3. 01背包问题
问题:

———————————————————————————————————————————
参考:
具体分析:
#include <iostream>
#include <algorithm>
using namespace std;
struct T//!结构体!
{
double weight;
double value;
double devide;
};
int n;
double c; //n件物品和背包容量c
double sum = 0, sumval = 0, bestval = 0; //sum:当前重量 sumval:当前价值 bestval:最大价值
T* t; //!结构体!
bool cmp(T t1, T t2)
{
return t1.devide > t2.devide;
}
int Bound(int y) //约束函数
{
int i = y;
double leftv = 0;
double leftw = c - sum;
while (i < n && t[i].weight <= leftw)
{
leftw -= t[i].weight;
leftv += t[i].value;
i++;
}
if (i < n) //背包装满
{
leftv += t[i].devide*leftw;
}
return leftv;
}
void Backtrack(int i)
{
if (i >= n) //递归终止条件
{
if (sumval > bestval)
{
bestval = sumval;
}
return;
}
if (sum + t[i].weight <= c)
{
sum += t[i].weight;
sumval += t[i].value;
Backtrack(i + 1);
sumval -= t[i].value;
sum -= t[i].weight;
}
//通过边界,剪枝
if (sumval + Bound(i + 1) > bestval)
{
Backtrack(i + 1);
}
}
int main()
{
cin >> n >> c;
t = new T[n];
for (int i = 0; i <n; i++)//!结构体!
{
cin >> t[i].weight >> t[i].value;
t[i].devide = t[i].value / t[i].weight;
}
sort(t, t+n, cmp); //剪枝优化,采取价值高的优先
Backtrack(0);
cout << bestval;
return 0;
}
问题:上面代码是最终通过的代码,不是早期错误版本。
- 耗时过多:无结构体版本,套用了子集和的框架,但耗时无法压下来。
想通过:优化剪枝(bound函数);排序(优先选取价值高的);来降低耗时 - 对C++的结构体不太清楚,直接借鉴了参考的代码。
- 注意Backtrack函数的参数从0还是从1开始;通过随便一个案例画图就可得知
从0开始,则终止条件为:i>=n
从1开始,则终止条件为:i>n
3.1 输出分析版
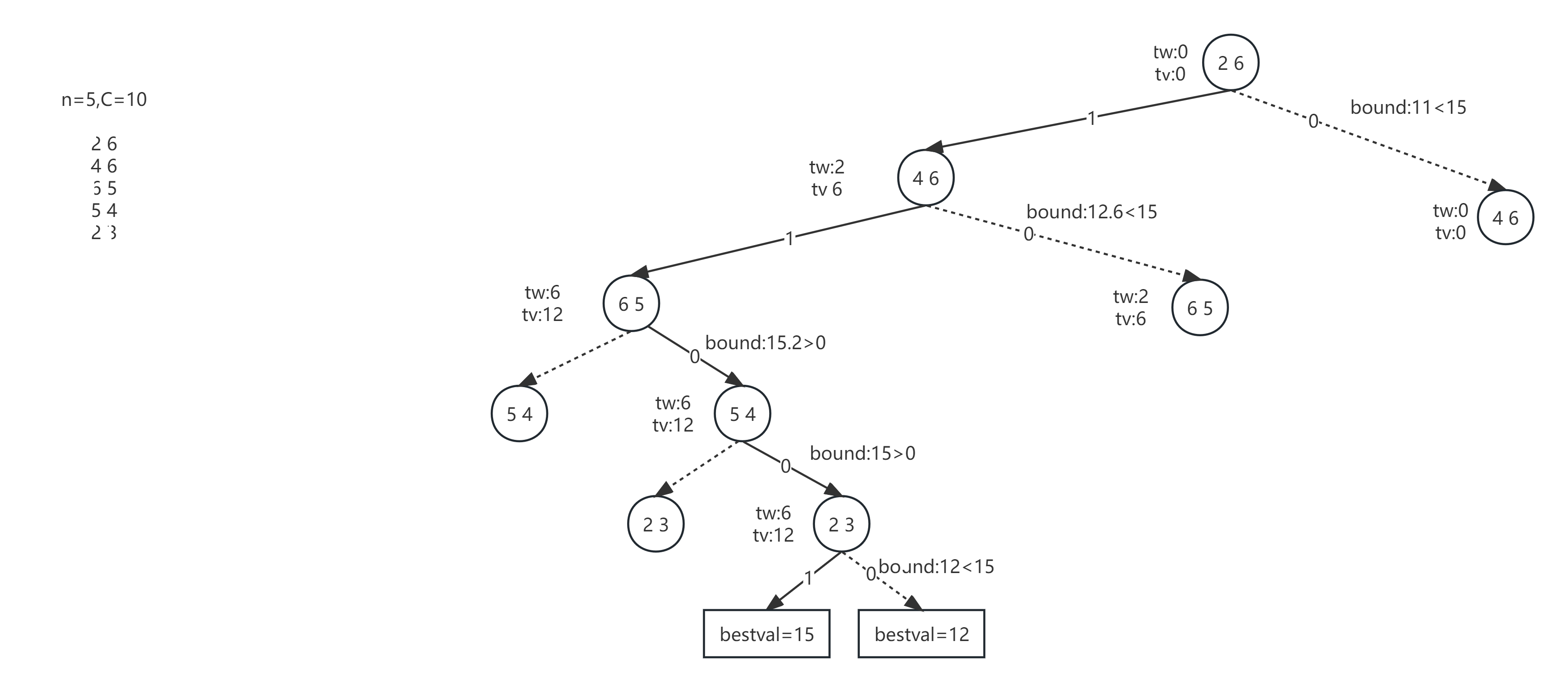
具体策略:
利用回溯=递归+剪枝,有选择的遍历解,从而获取特定解。
递归每个解的时候,利用剪枝策略:
左剪枝策略是当前和(不包括当前节点重量)+当前节点重量是否大于背包容量,当大于背包容量时,则说明左分支之后的解都是大于背包容量,可以不遍历;当小于或等于背包容量时,则说明左分支存在解。
右剪枝策略是计算,右分支能达到的最大背包价值是否大于当前最优背包价值,如果大于则说明右分支有解,如果小于则剪枝。
————————————————————
#include <iostream>
#include <algorithm>
using namespace std;
struct T
{
double weight;
double value;
double devide;
};
int n;
double c; //n件物品和背包容量c
double sum = 0, sumval = 0, bestval = 0; //sum:当前重量 sumval:当前价值 bestval:最大价值
T* t;
void swap(T *i,T *j){
T temp=*i;
*i=*j;
*j=temp;
}
void sort(T *t)
{
int i;
for (i = 0; i < n-1; i++) //
{
for (int j = 0; j < n-i-1; j++) //从0开始一直到len-i-1的是这次需要确认最大值数量
if (t[j].value < t[j+1].value)
{
swap(t[j],t[j+1]);
}
}
}
int Bound(int y) //约束函数
{
int i = y;
double leftv = 0;
double leftw = c - sum;
while (i < n && t[i].weight <= leftw)
{
leftw -= t[i].weight;
leftv += t[i].value;
i++;
}
if (i < n) //背包装满
{
leftv += t[i].devide*leftw;
}
return leftv;
}
void Backtrack(int i)
{ cout<<"当前结点"<<t[i].weight<<"\n";
if (i >= n) //递归终止条件
{ cout<<"判断叶子"<<endl;
if (sumval > bestval)
{ cout<<"判断最优"<<endl;
bestval = sumval;
}
return;
}
cout<<"进入"<<t[i].weight<<"左分支"<<endl;
if (sum + t[i].weight <= c)
{
sum += t[i].weight;
sumval += t[i].value;
Backtrack(i + 1);
sumval -= t[i].value;
sum -= t[i].weight;
}
cout<<"进入"<<t[i].weight<<"右分支"<<endl;
//通过边界,剪枝
double bound=Bound(i+1);
// cout<<"bound="<<sumval+bound<<" bestval="<<bestval<<"\n";
if (sumval + bound > bestval)
{
Backtrack(i + 1);
}
cout<<"结束"<<t[i].weight<<endl;
}
int main()
{
cin >> n >> c;
t = new T[n+1];
for (int i = 0; i <n; i++)
{
cin >> t[i].weight >> t[i].value;
t[i].devide = t[i].value / t[i].weight;
}
sort(t); //剪枝优化,采取价值高的优先
cout<<"排序后:";
for(int i=0;i<n;i++)
{
cout<<t[i].weight<<" "<<t[i].value<<"\n";
}
Backtrack(0);
cout << bestval;
return 0;
}
4 最优装载问题
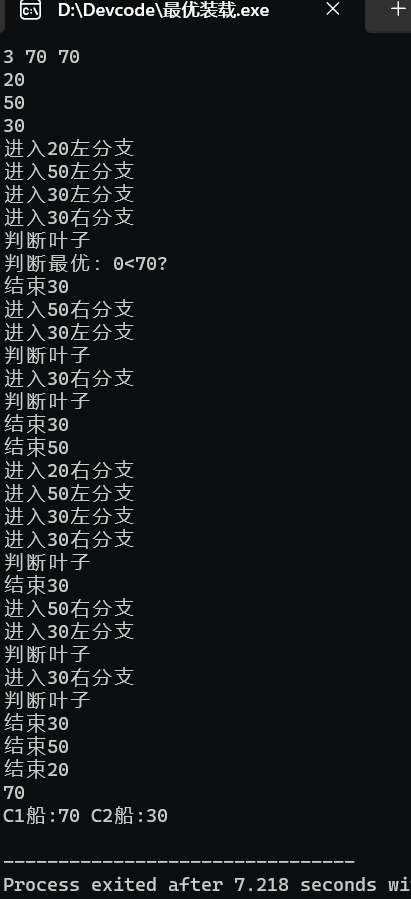
问题:
使用回溯法求解最优装载问题:集装箱数量n=3,两艘轮船的载重量C1=C2=70, 每个集装箱的重量W={20,50,30},其解空间由长度为3的0-1向量组成。请:(1)画出解空间树;(2)说明其搜索策略;(3) 给出详细求解过程;(4)给出最终的装载方案
——————————————————————————
参考
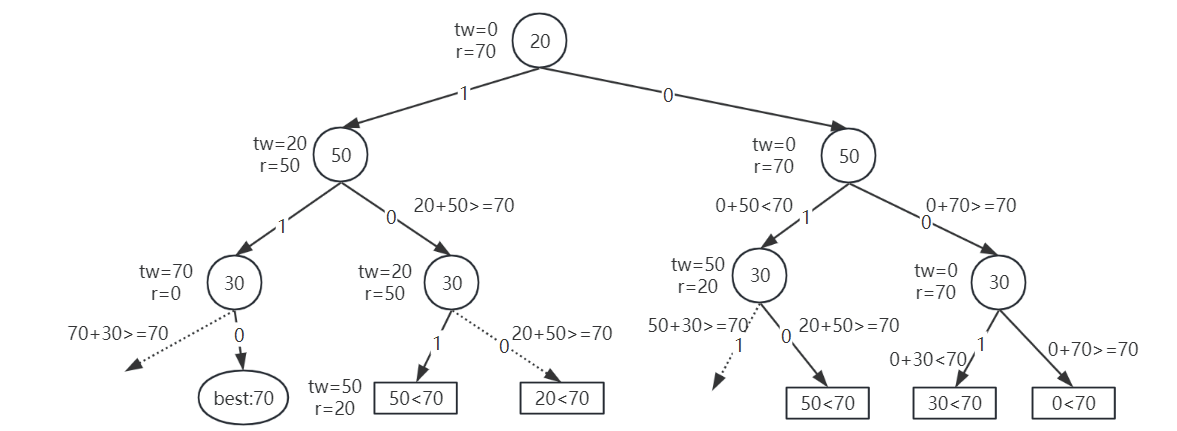
递归+剪枝策略;
左剪枝:当前节点重量+之前节点总重量是否大于C1,大于则剪枝;右剪枝:之前节点总重量加剩余节点重量(针对C1)是否小于C1最优重量,小于则剪枝;
#include <iostream>
using namespace std;
#define Max 101
int n,c1,c2;//集装箱数量,最大重量
int w[Max]={0};//重量数组
int a[Max];//方向数组
int tw=0;//当前重量和
int bestw=0;// 第一个集装箱最优承重
int r=0;//货物总重
void Backtrack(int i)
{ //终止条件
if(i>=n)
{ cout<<"判断叶子"<<endl;
if(tw>bestw)
{
cout<<"判断最优:"<<bestw<<"<"<<tw<<"?"<<endl;
bestw=tw;
}
return;
}
cout<<"进入"<<w[i]<<"左分支"<<endl;
//左剪枝,当前总重量+当前节点重量是否小于等于C1船容量,是则进入,不是则剪枝
if(tw+w[i]<=c1)
{
a[i]=1;
tw+=w[i];
Backtrack(i+1);
tw-=w[i];
}
cout<<"进入"<<w[i]<<"右分支" <<endl;
//右剪枝:当前总重量+剩余总重量是否大于最优总重量,大于等于则说明可能有解,小于等于则剪枝;
if(tw+(c1-tw)>=bestw) //最大容量是C1,得考虑这个问题
{
a[i]=0;
Backtrack(i+1);
}
cout<<"结束"<<w[i]<<endl;
}
int main()
{ cin>>n>>c1>>c2;
for(int i=0;i<n;i++)
{
cin>>w[i];
r+=w[i];
}
Backtrack(0);
cout<<bestw<<endl;
cout<<"C1船:"<<bestw<<" C2船:"<<r-bestw<<endl;
return 0;
}
分支限界法
1.背包问题
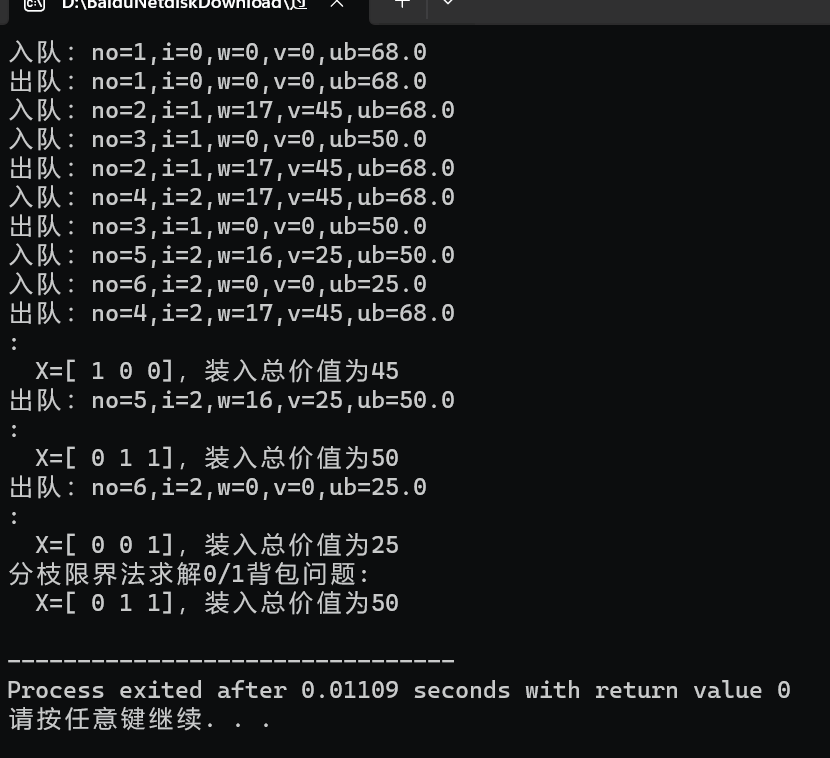
FIFO队列求解背包问题
解空间:
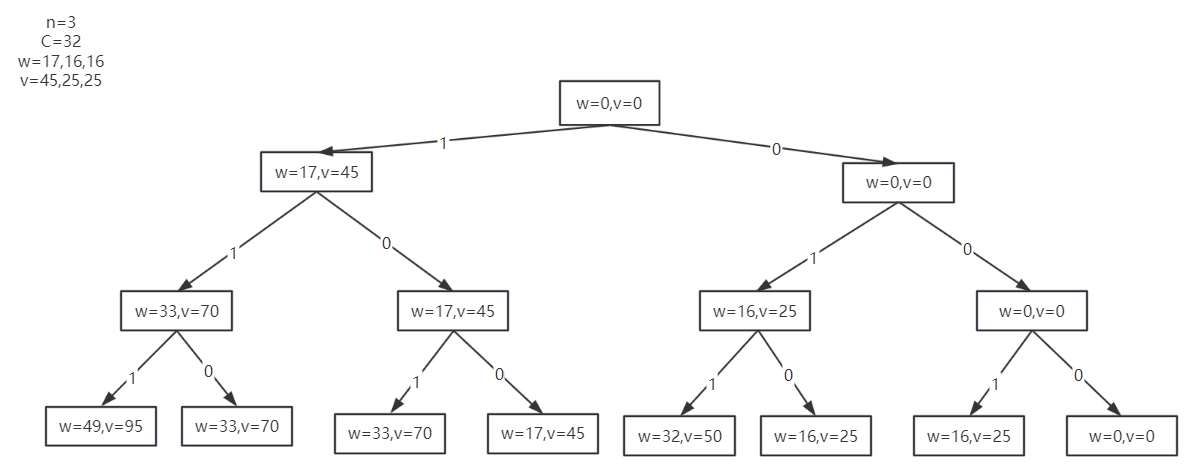
解空间(剪枝):
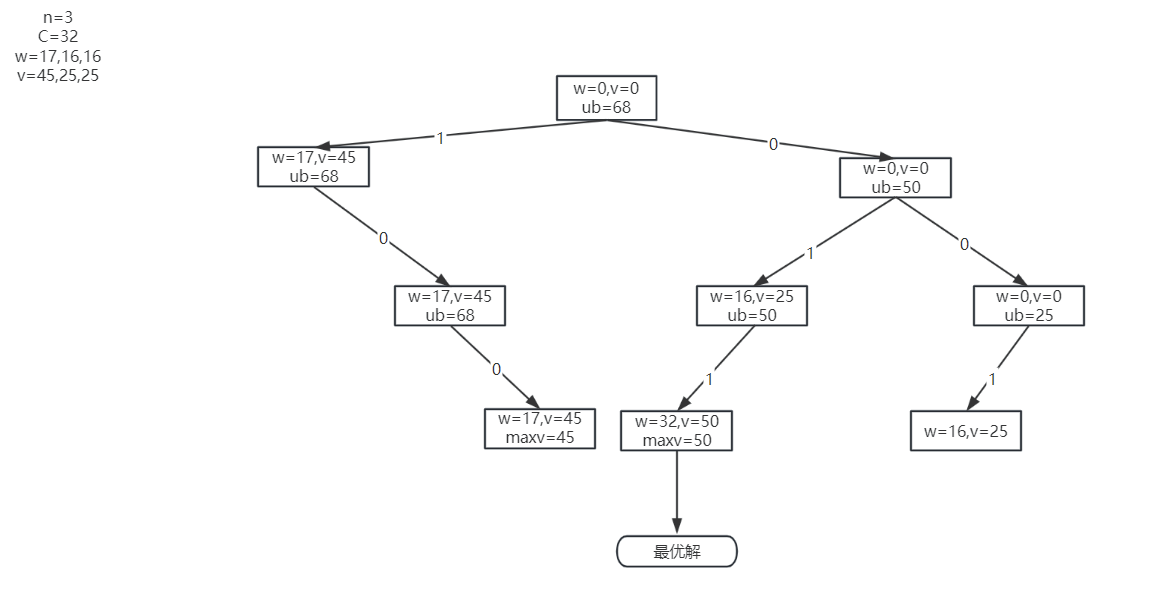
运行结果:
//采用队列式分枝限界法求解0/1背包问题的算法
#include <stdio.h>
#include <queue>
using namespace std;
#define MAXN 20 //最多可能物品数
//问题表示
int n=3,W=32;
int w[]={0,17,16,16}; //重量,下标0不用
int v[]={0,45,25,25}; //价值,下标0不用
//求解结果表示
int maxv=-9999; //存放最大价值,初始为最小值
int bestx[MAXN]; //存放最优解,全局变量
int total=1; //解空间中结点数累计,全局变量
struct NodeType //队列中的结点类型
{ int no; //结点编号
int i; //当前结点在搜索空间中的层次
int w; //当前结点的总重量
int v; //当前结点的总价值
int x[MAXN]; //当前结点包含的解向量
double ub; //上界
};
void bound(NodeType &e) //计算分枝结点e的上界
{
int i=e.i+1;
int sumw=e.w;
double sumv=e.v;
while ((sumw+w[i]<=W) && i<=n) //超重结束 || 遍历到头
{ sumw+=w[i]; //计算背包已装入载重
sumv+=v[i]; //计算背包已装入价值
i++;
}
if (i<=n)
e.ub=sumv+(W-sumw)*v[i]/w[i];
else
e.ub=sumv;
}
void output(NodeType e)
{
printf("no=%d,i=%d,w=%d,v=%d,ub=%.1f \n",e.no,e.i,e.w,e.v,e.ub);
}
void EnQueue(NodeType e,queue<NodeType> &qu) //结点e进队qu
{
if (e.i==n) //到达叶子结点
{
if (e.v>maxv) //找到更大价值的解
{
maxv=e.v;
for (int j=1;j<=n;j++) //更新最优解向量
bestx[j]=e.x[j];
}
printf(":\n X=["); //输出最优解
for(int i=1;i<=n;i++)
printf("%2d",e.x[i]); //输出所求X[n]数组
printf("],装入总价值为%d\n",e.v);
}
else {
printf("入队:");
output(e);
qu.push(e);
} //非叶子结点进队
}
void bfs() //求0/1背包的最优解
{
int j;
NodeType e,e1,e2; //定义3个结点
queue<NodeType> qu; //定义一个队列
e.i=0; //根结点置初值,其层次计为0
e.w=0;
e.v=0;
e.no=total++;
for (j=1;j<=n;j++) //当前节点的解向量初始化
e.x[j]=0;
bound(e); //求根结点的上界
//
printf("入队:");
output(e); //输出节点的状态
qu.push(e); //根结点进队
while (!qu.empty()) //队不空循环
{
e=qu.front(); //保留首节点
qu.pop(); //出队结点e
printf("出队:");
output(e);//输出节点状态
if (e.w+w[e.i+1]<=W) //剪枝:检查左孩子结点
{
e1.no=total++;
e1.i=e.i+1; //建立左孩子结点
e1.w=e.w+w[e1.i];
e1.v=e.v+v[e1.i];
for (j=1;j<=n;j++) //复制解向量
e1.x[j]=e.x[j];
e1.x[e1.i]=1;
bound(e1); //求左孩子结点的上界
EnQueue(e1,qu); //左孩子结点进队操作
}
e2.no=total++; //建立右孩子结点
e2.i=e.i+1;
e2.w=e.w;
e2.v=e.v;
for (j=1;j<=n;j++) //复制解向量
e2.x[j]=e.x[j];
e2.x[e2.i]=0;
bound(e2); //求右孩子结点的上界
if (e2.ub>maxv)
{//若右孩子结点可行,则进队,否则被剪枝
// printf("maxv=%d \n",maxv);
EnQueue(e2,qu);
}
}
}
int main()
{
bfs(); //调用队列式分枝限界法求0/1背包问题
printf("分枝限界法求解0/1背包问题:\n X=["); //输出最优解
for(int i=1;i<=n;i++)
printf("%2d",bestx[i]); //输出所求X[n]数组
printf("],装入总价值为%d\n",maxv);
return 0;
}
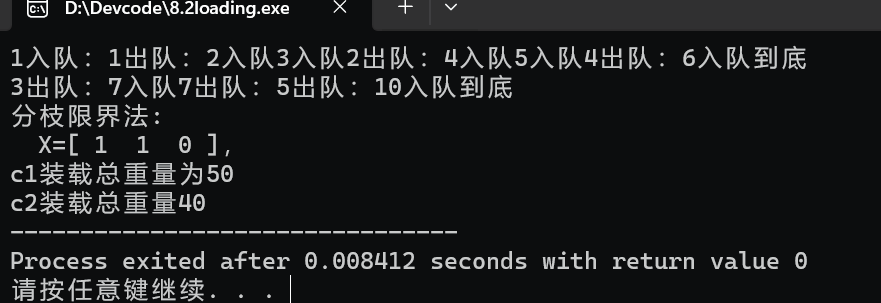
最优装载
优先队列求解最优装载
#include <stdio.h>
#include <queue>
#include <iostream>
using namespace std;
#define Max 20
int n=3,c1=50,c2=50;
int sumw=90;
int w[]={0,10,40,40};
int bestw=-1;
int bestx[Max];
int total=1;
struct NodeType
{
int no;
int i;
int w;
int x[Max];
double ub;
bool operator<(const NodeType &s) const //重载<关系函数
{
return ub<s.ub; //ub越大越优先出队
}
};
void bound(NodeType &e)
{
int i=e.i+1;
int sumw=e.w;
while((sumw+w[i]<=c1)&&i<=n)
{
sumw+=w[i];
i++;
}
e.ub=sumw;
}
void EnQueue(NodeType e,priority_queue<NodeType> &qu)
{
if(e.i==n)
{
if(e.w>bestw)
{
bestw=e.w;
for(int i=1;i<=n;i++)
bestx[i]=e.x[i];
}
cout<<"到底"<<endl;
// for(int i=1;i<=n;i++)
// {
// cout<<e.x[i]<<endl;
// }
}
else
{
qu.push(e);
}
}
void bfs()
{
int j;
NodeType e,e1,e2;
priority_queue<NodeType> qu;
e.i=0;
e.w=0;
e.no=total++;
for(j=1;j<=n;j++)
e.x[j]=0;
bound(e);
cout<<e.no<<"入队:";
qu.push(e);
while(!qu.empty())
{
e=qu.top();
qu.pop();
cout<<e.no<<"出队:";
if(e.w+w[e.i+1]<=c1)
{
e1.no=total++;
e1.i=e.i+1;
e1.w=e.w+w[e1.i];
for(j=1;j<=n;j++)
{
e1.x[j]=e.x[j];
}
e1.x[e1.i]=1;
bound(e1);
cout<<e1.no<<"入队";
EnQueue(e1,qu);
}
e2.no=total++;
e2.i=e.i+1;
e2.w=e.w;
for(j=1;j<=n;j++)
e2.x[j]=e.x[j];
e2.x[e2.i]=0;
if(e2.ub>bestw)
{
cout<<e2.no<<"入队";
EnQueue(e2,qu);
}
}
}
int main()
{
bfs();
printf("分枝限界法求解最优装载:\n X=[");
for(int i=1;i<=n;i++) //输出最优解
printf("%2d ",bestx[i]); //输出所求X[n]数组
printf("],\nc1装载总重量为%d\nc2装载总重量%d",bestw,(sumw-bestw));
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号