[algorithm] 如何计算一个树的最远点.
Description
有一颗 n个点的树，根节点序号是 1，其他节点的序号按照由上而下，由左往右的顺序排列。知道树中 n-1条边的长度。如何计算一个点到树中最远点的距离？
输入：第1行为节点数n，以下n-1行，每行两个整数，分别给出节点2到节点n的父节点和边权。
输出：n行，其中第i行为节点i到树中最远点的距离。
来自德问的一个题目，看到了就想了一下，其实就是一个dp，下面简要写一下算法思路，给出一个实例的分析过程。这里只针对二叉树做分析，多叉的情况处理方法类似。把树放平了看，可能好理解一点，求节点i到树中最远点的距离。
推导:
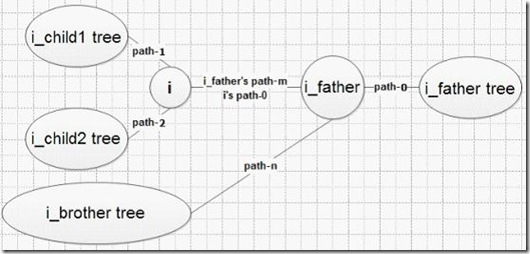
1: 从图中看，从i出发的路径有三条，分别是path-0,path-1,path-2，假设path-0是朝向父亲节点的(右边)，path-1和path-2朝向孩子节点的(左边)，方便叙述。顺着三个方向到“该方向上最远点”的距离假设为dis(i,0),dis(i,1),dis(i,2)，那么到最远点的距离是max(dis(i,0),dis(i,1),path(i,2))；
2: dis(i,1),dis(i,2)总是有一个是比较大的(后面会看到，在算法中可以很简单的通过比较得到)，我们将长度较大的路径命名为path-1路径，那么到i节点到最远点的距离变为: max(dis(i,0),dis(i,1))，因为dis(i,1)总是大于dis(i,2)，不在参与比较。
3: 简单推导几个方程式:
(1) i节点沿着path-1方向的最远距离是i与i_child1之间的距离 + i_child1沿着path-1方向的最远距离
得到：dis(i,1) = distance(i,i_child1) + dis(i_child1,1);
(2) i节点沿着path-2方向的最远距离是i与i_child2之间的距离 + i_child2沿着path-1(# 03/25/2012修正)方向的最远距离
得到：dis(i,2) = distance(i,i_child2) + dis(i_child2,1);
(3) i节点沿着path-0方向的最远距离是i与i_father之间的距离 + max ( i_father沿着path-0的最远距离，i_father沿着path-n的距离)；
这里的n暂时不确定是1还是2，因为我们并不知道i是在i_father的path-1方向还是path-2方向，信息可通过记录dis(i,1)通过的直接孩子节点获取。
得到：dis(i,0) = distance(i,i_father) + max(dis(i_father，0)，dis(i_father,n));如果i在path-1上，则n=2，如果i在path-2上，则n=1。
算法流程:
1: 左到右(对树而言由下至上)，针对每一个节点计算: dis(i,1)和dis(i,2)
2: 右到左(对树而言由上至下)，针对每一个节点计算: dis(i,0)
3: 最后max(dis(i,0),dis(i,1))得到结果
实例:
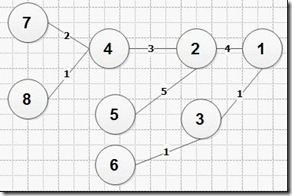
1: dis(i,1)和dis(i,2)
dis(7,1) = 0; dis(7,2) = 0; dis(8,1) = 0; dis(8,2) = 0;
dis(4,1) = 2;dis(4,2) = 1;dis(5,1) = 0;dis(5,2) = 0;dis(6,1) = 0;dis(6,2) = 0;
dis(2,1) = 5;dis(2,2) = 5;dis(3,1) = 1;dis(3,2) = 0;
dis(1,1) = 9;dis(1,2) = 2;
2: dis(0)
dis(1,0) =0;
2节点位于father的path-1上,n=2:
dis(2,0) = distance(2,1)+max(dis(1,0),dis(1,2)) = 4+max(0,2)=6;
3节点位于father的path-2上，n=1:
dis(3,0) = distance(3,1)+max(dis(1,0),dis(1,1))=1+max(0,9) =10;
4节点位于father的path-1上，n=2:
dis(4,0) = distance(4,2)+max(dis(2,0),dis(2,2)) = 3+max(6,5)=9;
5节点位于father的path-2上，n=1:
dis(5,0) = distance(5,2)+max(dis(2,0),dis(2,1)) = 5+max(6,5)=11;
6节点位于father的path-1上,n=2;
dis(6,0)=distance(6,3)+max(dis(3,0),dis(3,2))=1+max(10,0)=11;
7节点位于father的path-1上,n=2;
dis(7,0)=distance(7,4)+max(dis(4,0),dis(4,2))=2+max(9,1)=11;
8节点位于father的path-2上,n=1;
dis(8,0)=distance(8,4)+max(dis(4,0),dis(4,1))=1+max(9,2)=10;
3: max(dis(i,0),dis(i,1))得到: 节点-最远距离
1-9;2-6;3-10;4-9;5-11;6-11;7-11;8-10
