线性表的顺序存储和实现

1.线性表的顺序存储表示

• 顺序存储：逻辑相邻，物理也相邻的存储结构。用一组地址连续的存储单元依次存放线性表中的数据元素。可通过静态数组V[n]或动态数组来实现。
• 地址计算公式：LOC(ai) = LOC(a0)基地址 + i×C相同数据类型占用相同大小的空间。
• 顺序表的特点：

       （1）存储密度高：存储密度=数据元素的值所需的存储空间/该元素实际所需的存储空间。但是需要预先分配“足够多”的空间，这可能会造成存储空间的浪费。

       （2）便于随机存取。

       （3）不便于插入和删除操作，因为会引起大量结点的移动。

2.顺序表类的描述

• 数组空间应根据实际需要定义为“足够大”，设为maxSize。考虑到线性表的长度是可变的，故还需要用一个变量curLen来纪录线性表当前的实际长度。
• Java代码实现：

点击查看代码

package LinearList;

public class SqList implements IList{
	
	private Object[] listElem;
	private int curLen;
	
	public SqList(int maxSize) {
		curLen = 0;
		listElem = new Object[maxSize];
	}
}

3.顺序表上基本操作的实现

• Java代码实现：

点击查看代码

package LinearList;

public class SqList implements IList{
	
	private Object[] listElem;
	private int curLen;
	
	public SqList(int maxSize) {
		curLen = 0;
		listElem = new Object[maxSize];
	}
	
	public void clear() {
		curLen = 0;
	}
	
	public boolean isEmpty() {
		return curLen == 0;
	}
	
	public int getLength() {
		return curLen;
	}
	
	public Object getValue(int i) throws Exception{
		if(i<0 || i>curLen-1)
			throw new Exception("第"+i+"个元素不存在");
		return listElem[i];		
	}
	
	public void display() {
		for(int j=0;j<curLen;j++) 
			System.out.println(listElem[j]);
	}
	
	public void expandSpace(int newMaxSize) {
		Object[] newArr = new Object[newMaxSize];
		for(int i=0;i<listElem.length;i++)
			newArr[i]=listElem[i];
		listElem = newArr;
	}
	
	public void insert(int i,Object x) throws Exception{
		if(curLen == listElem.length)
			throw new Exception("顺序表已满");
		if(i<0 || i>curLen)
			throw new Exception("插入位置不合法");
		for(int j=0;j>i;j--)
			listElem[j]=listElem[j-1];
		listElem[i]=x;
		curLen++;
	}
	
	public void remove(int i)throws Exception{
		if(i<0 || i>curLen-1)
			throw new Exception("删除位置不合法");
		for(int j=i;j<curLen-1;j++)
			listElem[j]=listElem[j+1];
		curLen--;
	}
	
	public int indexOf(Object x) {
		int j=0;
		while(j<curLen && !listElem[j].equals(x))
			j++;
		if(j<curLen)
			return j;
		else
			return -1;
	}

}

4.其中几个重要方法介绍与算法的性能分析

1.插入操作：在第i个元素ai之前插入一个值为x的元素，其中0≤i≤curLen。当i=0时，在表头插入；当i=curLen时，在表尾插入。

算法步骤：

（1）检测空间是否已满，若已满则抛出异常或调用扩容方法。

（2）判断参数i的合法性，当0≤i≤curLen时合法。

（3）插入位置及之后的所有元素后移一个位置。注意：必须先从最后一个数据元素开始逐个后移。

（4）插入元素，表长加1。

性能分析：在第i个数据元素之前插入，会引起n-i个数据元素向后移动。假设在第 i 个元素之前插入的概率为Pi ,则在等概率的情况下，移动元素的平均次数为：

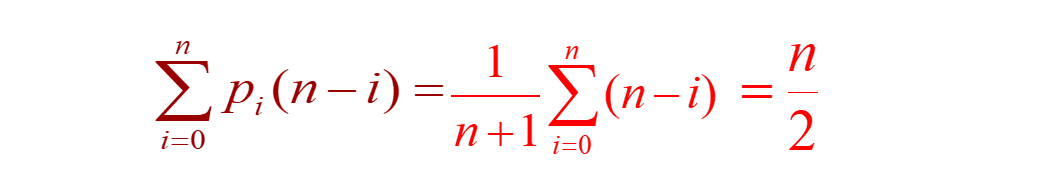
所以时间复杂度为O(n)。

2.删除操作：将第i个位置上的数据元素从顺序表中删除。

算法步骤：

（1）判断参数i的合法性，若i < 0 || i >curLen-1时不合法，抛出异常。

（2）将第i个元素之后的所有元素前移一个位置。

（3）表长减1。

性能分析：删除第i个数据元素会引起n-1-i个数据元素前移。假设删除第i个元素的概率为 p_i ，则在等概率的情况下，移动元素的平均次数为：

                      

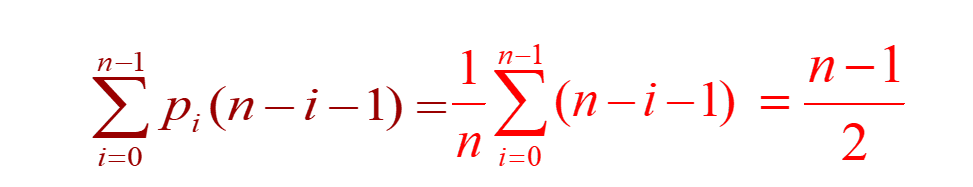
所以时间复杂度为O(n)。

3.按值查找操作：查找数据元素x在顺序表中是否存在,若存在则返回x初次出现的位置,否则返回-1。  

          算法步骤：将每一个元素从头依次进行比较，有相等则返回该元素的位序号，否则返回-1。

          性能分析：如果待查找的数据元素x在顺序表中第 i  个位置上，则需比较i+1次，所以在等概率条件下，数据元素的平均比较次数为：

     

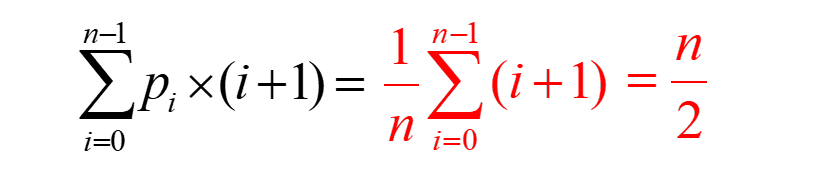
          所以时间复杂度为O(n)。

5.本节小结

数组的实现可以使得随机存取操作仅花费常数时间，遍历线性表会以线性时间被执行。不过插入和删除的花费却过于昂贵，平均要移动一半元素，因此需要线性时间。另一方面，如果所有的操作都发生在表的高端，那就没有元素需要移动，插入与删除仅需要花费O(1)的时间。

存在许多实际情形（如花名册），表通常是在高端进行插入操作而建成，其后只发生对数组的访问。在这种情况下，数组顺序表是一种恰当的实现。然而，如果经常对表的进行插入与删除操作（特别是在前端），这就不是一种好的选择。