kalman滤波
kalman滤波原理(通俗易懂)
1. 在学习卡尔曼滤波器之前,首先看看为什么叫“卡尔曼”。跟其他著名的理论(例如傅立叶变换,泰勒级数等等)一样,卡尔曼也是一个人的名字,而跟他们不同的是,他是个现代人!
卡尔曼全名Rudolf Emil Kalman,匈牙利数学家,1930年出生于匈牙利首都布达佩斯。1953,1954年于麻省理工学院分别获得电机工程学士及硕士学位。1957年于哥伦比亚大学获得博士学位。我们现在要学习的卡尔曼滤波器,正是源于他的博士论文和1960年发表的论文《A New Approach to Linear Filtering and Prediction Problems》(线性滤波与预测问题的新方法)。如果对这编论文有兴趣,可以到这里的地址下载:http://www.cs.unc.edu/~welch/kalman/media/pdf/Kalman1960.pdf
简单来说,卡尔曼滤波器是一个“optimal recursive data processing
algorithm(最优化自回归数据处理算法)”。对于解决很大部分的问题,他是最优,效率最高甚至是最有用的。他的广泛应用已经超过30年,包括机器人导航,控制,传感器数据融合甚至在军事方面的雷达系统以及导弹追踪等等。近年来更被应用于计算机图像处理,例如头脸识别,图像分割,图像边缘检测等等。
2.卡尔曼滤波器的介绍
(Introduction to the Kalman Filter)
为了可以更加容易的理解卡尔曼滤波器,这里会应用形象的描述方法来讲解,而不是像大多数参考书那样罗列一大堆的数学公式和数学符号。但是,他的5条公式是其核心内容。结合现代的计算机,其实卡尔曼的程序相当的简单,只要你理解了他的那5条公式。
在介绍他的5条公式之前,先让我们来根据下面的例子一步一步的探索。
假设我们要研究的对象是一个房间的温度。根据你的经验判断,这个房间的温度是恒定的,也就是下一分钟的温度等于现在这一分钟的温度(假设我们用一分钟来做时间单位)。假设你对你的经验不是100%的相信,可能会有上下偏差几度。我们把这些偏差看成是高斯白噪声(White
Gaussian Noise),也就是这些偏差跟前后时间是没有关系的而且符合高斯分配(Gaussian
Distribution)。另外,我们在房间里放一个温度计,但是这个温度计也不准确的,测量值会比实际值偏差。我们也把这些偏差看成是高斯白噪声。
好了,现在对于某一分钟我们有两个有关于该房间的温度值:你根据经验的预测值(系统的预测值)和温度计的值(测量值)。下面我们要用这两个值结合他们各自的噪声来估算出房间的实际温度值。
假如我们要估算k时刻的是实际温度值。首先你要根据k-1时刻的温度值,来预测k时刻的温度。因为你相信温度是恒定的,所以你会得到k时刻的温度预测值是跟k-1时刻一样的,假设是23度,同时该值的高斯噪声的偏差是5度(5是这样得到的:如果k-1时刻估算出的最优温度值的偏差是3,你对自己预测的不确定度是4度,他们平方相加再开方,就是5)。然后,你从温度计那里得到了k时刻的温度值,假设是25度,同时该值的偏差是4度。
由于我们用于估算k时刻的实际温度有两个温度值,分别是23度和25度。究竟实际温度是多少呢?相信自己还是相信温度计呢?究竟相信谁多一点,我们可以用他们的covariance来判断。因为Kg^2=5^2/(5^2+4^2),所以Kg=0.78,我们可以估算出k时刻的实际温度值是:23+0.78*(25-23)=24.56度。可以看出,因为温度计的covariance比较小(比较相信温度计),所以估算出的最优温度值偏向温度计的值。
现在我们已经得到k时刻的最优温度值了,下一步就是要进入k+1时刻,进行新的最优估算。到现在为止,好像还没看到什么自回归的东西出现。对了,在进入k+1时刻之前,我们还要算出k时刻那个最优值(24.56度)的偏差。算法如下:((1-Kg)*5^2)^0.5=2.35。这里的5就是上面的k时刻你预测的那个23度温度值的偏差,得出的2.35就是进入k+1时刻以后k时刻估算出的最优温度值的偏差(对应于上面的3)。
就是这样,卡尔曼滤波器就不断的把covariance递归,从而估算出最优的温度值。他运行的很快,而且它只保留了上一时刻的covariance。上面的Kg,就是卡尔曼增益(Kalman Gain)。他可以随不同的时刻而改变他自己的值,是不是很神奇!
下面就要言归正传,讨论真正工程系统上的卡尔曼。
3. 卡尔曼滤波器算法
(The Kalman Filter Algorithm)
在这一部分,我们就来描述源于Dr Kalman
的卡尔曼滤波器。下面的描述,会涉及一些基本的概念知识,包括概率(Probability),随即变量(Random
Variable),高斯或正态分配(Gaussian Distribution)还有State-space
Model等等。但对于卡尔曼滤波器的详细证明,这里不能一一描述。
首先,我们先要引入一个离散控制过程的系统。该系统可用一个线性随机微分方程(Linear Stochastic Difference equation)来描述:
X(k)=A X(k-1)+B U(k)+W(k)
再加上系统的测量值:
Z(k)=H X(k)+V(k)
上两式子中,X(k)是k时刻的系统状态,U(k)是k时刻对系统的控制量。A和B是系统参数,对于多模型系统,他们为矩阵。Z(k)是k时刻的测量值,H是测量系统的参数,对于多测量系统,H为矩阵。W(k)和V(k)分别表示过程和测量的噪声。他们被假设成高斯白噪声(White
Gaussian Noise),他们的covariance 分别是Q,R(这里我们假设他们不随系统状态变化而变化)。
对于满足上面的条件(线性随机微分系统,过程和测量都是高斯白噪声),卡尔曼滤波器是最优的信息处理器。下面我们来用他们结合他们的covariances 来估算系统的最优化输出(类似上一节那个温度的例子)。
首先我们要利用系统的过程模型,来预测下一状态的系统。假设现在的系统状态是k,根据系统的模型,可以基于系统的上一状态而预测出现在状态:
X(k|k-1)=A X(k-1|k-1)+B U(k) ……….. (1)
式(1)中,X(k|k-1)是利用上一状态预测的结果,X(k-1|k-1)是上一状态最优的结果,U(k)为现在状态的控制量,如果没有控制量,它可以为0。
到现在为止,我们的系统结果已经更新了,可是,对应于X(k|k-1)的covariance还没更新。我们用P表示covariance:
P(k|k-1)=A P(k-1|k-1) A’+Q ……… (2)
式(2)中,P(k|k-1)是X(k|k-1)对应的covariance,P(k-1|k-1)是X(k-1|k-1)对应的covariance,A’表示A的转置矩阵,Q是系统过程的covariance。式子1,2就是卡尔曼滤波器5个公式当中的前两个,也就是对系统的预测。
现在我们有了现在状态的预测结果,然后我们再收集现在状态的测量值。结合预测值和测量值,我们可以得到现在状态(k)的最优化估算值X(k|k):
X(k|k)= X(k|k-1)+Kg(k) (Z(k)-H X(k|k-1)) ……… (3)
其中Kg为卡尔曼增益(Kalman Gain):
Kg(k)= P(k|k-1) H’ / (H P(k|k-1) H’ + R) ……… (4)
到现在为止,我们已经得到了k状态下最优的估算值X(k|k)。但是为了要另卡尔曼滤波器不断的运行下去直到系统过程结束,我们还要更新k状态下X(k|k)的covariance:
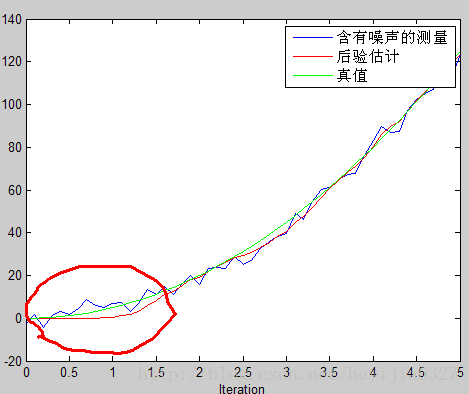
P(k|k)=(I-Kg(k) H)P(k|k-1) ……… (5)
其中I 为1的矩阵,对于单模型单测量,I=1。当系统进入k+1状态时,P(k|k)就是式子(2)的P(k-1|k-1)。这样,算法就可以自回归的运算下去。
卡尔曼滤波器的原理基本描述了,式子1,2,3,4和5就是他的5 个基本公式。根据这5个公式,可以很容易的实现计算机的程序。
下面,我会用程序举一个实际运行的例子。。。
4. 简单例子
(A Simple Example)
这里我们结合第二第三节,举一个非常简单的例子来说明卡尔曼滤波器的工作过程。所举的例子是进一步描述第二节的例子,而且还会配以程序模拟结果。
根据第二节的描述,把房间看成一个系统,然后对这个系统建模。当然,我们见的模型不需要非常地精确。我们所知道的这个房间的温度是跟前一时刻的温度相同的,所以A=1。没有控制量,所以U(k)=0。因此得出:
X(k|k-1)=X(k-1|k-1) ……….. (6)
式子(2)可以改成:
P(k|k-1)=P(k-1|k-1) +Q ……… (7)
因为测量的值是温度计的,跟温度直接对应,所以H=1。式子3,4,5可以改成以下:
X(k|k)= X(k|k-1)+Kg(k) (Z(k)-X(k|k-1)) ……… (8)
Kg(k)= P(k|k-1) / (P(k|k-1) + R) ……… (9)
P(k|k)=(1-Kg(k))P(k|k-1) ……… (10)
现在我们模拟一组测量值作为输入。假设房间的真实温度为25度,我模拟了200个测量值,这些测量值的平均值为25度,但是加入了标准偏差为几度的高斯白噪声(在图中为蓝线)。
为了令卡尔曼滤波器开始工作,我们需要告诉卡尔曼两个零时刻的初始值,是X(0|0)和P(0|0)。他们的值不用太在意,随便给一个就可以了,因为随着卡尔曼的工作,X会逐渐的收敛。但是对于P,一般不要取0,因为这样可能会令卡尔曼完全相信你给定的X(0|0)是系统最优的,从而使算法不能收敛。我选了X(0|0)=1度,P(0|0)=10。
该系统的真实温度为25度,图中用黑线表示。图中红线是卡尔曼滤波器输出的最优化结果(该结果在算法中设置了Q=1e-6,R=1e-1)。
附matlab下面的kalman滤波程序:
clear
N=200;
w(1)=0;
w=randn(1,N)
x(1)=0;
a=1;
for k=2:N;
x(k)=a*x(k-1)+w(k-1);
end
V=randn(1,N);
q1=std(V);
Rvv=q1.^2;
q2=std(x);
Rxx=q2.^2;
q3=std(w);
Rww=q3.^2;
c=0.2;
Y=c*x+V;
p(1)=0;
s(1)=0;
for t=2:N;
p1(t)=a.^2*p(t-1)+Rww;
b(t)=c*p1(t)/(c.^2*p1(t)+Rvv);
s(t)=a*s(t-1)+b(t)*(Y(t)-a*c*s(t-1));
p(t)=p1(t)-c*b(t)*p1(t);
end
t=1:N;
plot(t,s,'r',t,Y,'g',t,x,'b');
卡尔曼滤波 -- 从推导到应用(一)
前言
卡尔曼滤波器是在估计线性系统状态的过程中,以最小均方误差为目的而推导出的几个递推数学等式,也可以从贝叶斯推断的角度来推导。
本文将分为两部分:
第一部分,结合例子,从最小均方误差的角度,直观地介绍卡尔曼滤波的原理,并给出较为详细的数学推导。
第二部分,通过两个例子给出卡尔曼滤波的实际应用。其中将详细介绍一个匀加速模型,并直观的对比系统状态模型的建立对滤波的影响。
第一部分
先看一个对理解卡尔曼滤波能起到作用的的笑话:
一片绿油油的草地上有一条曲折的小径,通向一棵大树.一个要求被提出:从起点沿着小径走到树下.
“很简单.” A说,于是他丝毫不差地沿着小径走到了树下.
现在,难度被增加了:蒙上眼。
“也不难,我当过特种兵。” B说,于是他歪歪扭扭地走到了树旁。“唉,好久不练,生疏了。” (只凭自己的预测能力)
“看我的,我有 DIY 的 GPS!” C说,于是他像个醉汉似地歪歪扭扭的走到了树旁。“唉,这个 GPS 没做好,漂移太大。”(只依靠外界有很大噪声的测量)
“我来试试。” 旁边一也当过特种兵的拿过 GPS, 蒙上眼,居然沿着小径很顺滑的走到了树下。(自己能预测+测量结果的反馈)
“这么厉害!你是什么人?”“卡尔曼 ! ”
“卡尔曼?!你就是卡尔曼?”众人大吃一惊。
“我是说这个 GPS 卡而慢。”
此段引用自 highgear 的 《授之以渔:卡尔曼滤波器...大泄蜜...》 (点击可跳转到该网页)
这个小笑话很有意思的指出了卡尔曼滤波的核心,预测+测量反馈,记住这种思想。
-----------------------------------------------------------分割线-----------------------------------------------------------------------
在介绍卡尔曼滤波前,简单说明几个在学卡尔曼过程中要用到的概念。即什么是协方差,它有什么含义,以及什么叫最小均方误差估计,什么是多元高斯分布。如果对这些有了了解,可以跳过,直接到下面的分割线。
均方误差:它是"误差"的平方的期望值(误差就是每个估计值与真实值的差),也就是多个样本的时候,均方误差等于每个样本的误差平方再乘以该样本出现的概率的和。
方差:方差是描述随机变量的离散程度,是变量离期望值的距离。
注意两者概念上稍有差别,当你的样本期望值就是真实值时,两者又完全相同。最小均方误差估计就是指估计参数时要使得估计出来的模型和真实值之间的误差平方期望值最小。
两个实变量之间的协方差:
它表示的两个变量之间的总体误差,当Y=X的时候就是方差。下面说说我对协方差的通俗理解,先抛去公式中的期望不谈,即假设样本X,Y发生的概率就是1,那么协方差的公式就变成了:
这就是两个东西相乘,马上联想到数值图像里的相关计算。如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。协方差矩阵只不过就是元素多了组成了矩阵,其中协方差矩阵的对角线就是方差,具体公式形式请见wiki。
其实,这种相乘的形式也有点类似于向量投影,即两个向量的内积。再远一点,联想到傅里叶变换里频谱系数的确定,要确定一个函数f(x)在某个频率w上的频谱,就是<f(x),cos(wt)>,< ,>表示向量内积,通俗的讲是将f(x)投影到cos(wt)上,要讲清傅里叶的本质需要另写一篇博文,这里提到这些只是觉得有益于对知识的相互理解。
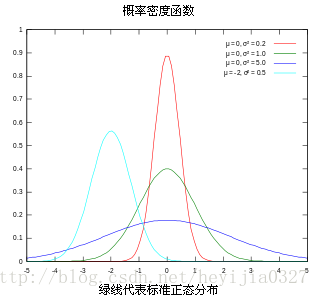
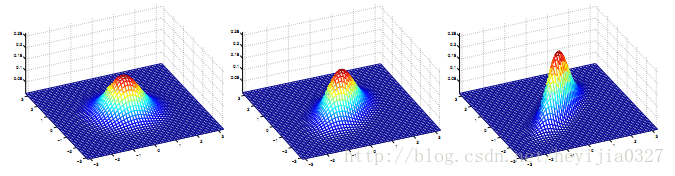
高斯分布:概率密度函数图像如下图,四条曲线的方差各不相同,方差决定了曲线的胖瘦高矮。(图片来源:维基百科)
多元高斯分布:就是高斯分布的低维向高维的扩展,图像如下。
对应多元高斯分布的公式也请自行谷歌,以前高斯公式中的方差也变成了协方差,对应上面三张图的协方差矩阵分别如下:
注意协方差矩阵的主对角线就是方差,反对角线上的就是两个变量间的协方差。就上面的二元高斯分布而言,协方差越大,图像越扁,也就是说两个维度之间越有联系。
-----------------------------------------------------------分割线---------------------------------------------------------------------
这部分每讲一个数学性的东西,接着就会有相应的例子和直观的分析帮助理解。
首先假设我们知道一个线性系统的状态差分方程为
其中x是系统的状态向量,大小为n*1列。A为转换矩阵,大小为n*n。u为系统输入,大小为k*1。B是将输入转换为状态的矩阵,大小为n*k。随机变量w为系统噪声。注意这些矩阵的大小,它们与你实际编程密切相关。
看一个具体的匀加速运动的实例。
有一个匀加速运动的小车,它受到的合力为 ft , 由匀加速运动的位移和速度公式,能得到由 t-1 到 t 时刻的位移和速度变化公式:
该系统系统的状态向量包括位移和速度,分别用 xt 和 xt的导数 表示。控制输入变量为u,也就是加速度,于是有如下形式:
所以这个系统的状态的方程为:
这里对应的的矩阵A大小为 2*2 ,矩阵B大小为 2*1。
貌似有了这个模型就能完全估计系统状态了,速度能计算出,位移也能计算出。那还要卡尔曼干嘛,问题是很多实际系统复杂到根本就建不了模。并且,即使你建立了较为准确的模型,只要你在某一步有误差,由递推公式,很可能不断将你的误差放大A倍(A就是那个状态转换矩阵),以至于最后得到的估计结果完全不能用了。回到最开始的那个笑话,如果那个完全凭预测的特种兵在某一步偏离了正确的路径,当他站在错误的路径上(而他自己以为是正确的)做下一步预测时,肯定走的路径也会错了,到最后越走越偏。
既然如此,我们就引进反馈。从概率论贝叶斯模型的观点来看前面预测的结果就是先验,测量出的结果就是后验。
测量值当然是由系统状态变量映射出来的,方程形式如下:
注意Z是测量值,大小为m*1(不是n*1,也不是1*1,后面将说明),H也是状态变量到测量的转换矩阵。大小为m*n。随机变量v是测量噪声。
同时对于匀加速模型,假设下车是匀加速远离我们,我们站在原点用超声波仪器测量小车离我们的距离。
也就是测量值直接等于位移。可能又会问,为什么不直接用测量值呢?测量值噪声太大了,根本不能直接用它来进行计算。试想一个本来是朝着一个方向做匀加速运动的小车,你测出来的位移确是前后移动(噪声影响),只根据测量的结果,你就以为车子一会往前开一会往后开。
对于状态方程中的系统噪声w和测量噪声v,假设服从如下多元高斯分布,并且w,v是相互独立的。其中Q,R为噪声变量的协方差矩阵。
看到这里自然要提个问题,为什么噪声模型就得服从高斯分布呢?请继续往下看。
对于小车匀加速运动的的模型,假设系统的噪声向量只存在速度分量上,且速度噪声的方差是一个常量0.01,位移分量上的系统噪声为0。测量值只有位移,它的协方差矩阵大小是1*1,就是测量噪声的方差本身。
那么:
Q中,叠加在速度上系统噪声方差为0.01,位移上的为0,它们间协方差为0,即噪声间没有关联。
理论预测(先验)有了,测量值(后验)也有了,那怎么根据这两者得到最优的估计值呢?首先想到的就是加权,或者称之为反馈。
我们认定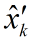
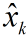
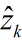
其中,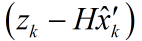
现在的关键就是求取这个K。这时最小均方误差就起到了作用,顺便在这里回答为什么噪声必须服从高斯分布,在进行参数估计的时候,估计的一种标准叫最大似然估计,它的核心思想就是你手里的这些相互间独立的样本既然出现了,那就说明这些样本概率的乘积应该最大(概率大才出现嘛)。如果样本服从概率高斯分布,对他们的概率乘积取对数ln后,你会发现函数形式将会变成一个常数加上样本最小均方误差的形式。因此,看似直观上很容易理解的最小均方误差理论上来源就出于那里(详细过程还请自行谷歌,请原谅,什么都讲的话就显得这边文章没有主次了)。
先看估计值和真实值间误差的协方差矩阵,提醒一下协方差矩阵的对角线元素就是方差,求这个协方差矩阵,就是为了利用他的对角线元素的和计算得到均方差.
这里请注意ek是向量,它由各个系统状态变量的误差组成。如匀加速运动模型里,ek便是由位移误差和速度误差,他们组成的协方差矩阵。表示如下:
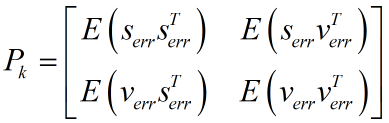
其中,Serr代表位移误差,Verr代表速度误差,对角线上就是各自的方差。
把前面得到的估计值代入这里能够化简得:
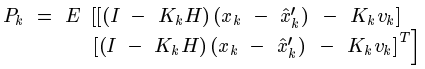
同理,能够得到预测值和真实值之间误差的协方差矩阵:
注意到系统状态x变量和测量噪声之间是相互独立的。于是展开(1)式可得:
最后得到:
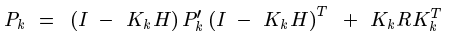
继续展开:
接下来最小均方差开始正式登场了,回忆之前提到的,协方差矩阵的对角线元素就是方差。这样一来,把矩阵P的对角线元素求和,用字母T来表示这种算子,他的学名叫矩阵的迹。
最小均方差就是使得上式最小,对未知量K求导,令导函数等于0,就能找到K的值。
注意这个计算式K,转换矩阵H式常数,测量噪声协方差R也是常数。因此K的大小将与预测值的误差协方差有关。不妨进一步假设,上面式子中的矩阵维数都是1*1大小的,并假设H=1,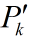
所以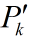
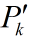
将计算出的这个K反代入Pk中,就能简化Pk,估计协方差矩阵Pk的:
因此递推公式中每一步的K就计算出来了,同时每一步的估计协方差也能计算出来。但K的公式中好像又多了一个我们还未曾计算出来的东西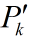
请先注意到预测值的递推形式是:
由于系统状态变量和噪声之间是独立,故可以写成:
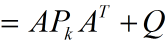
由此也得到了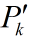
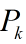
这里总结下递推的过程,理一下思路:
首先要计算预测值、预测值和真实值之间误差协方差矩阵。
有了这两个就能计算卡尔曼增益K,再然后得到估计值,
最后还要计算估计值和真实值之间的误差协方差矩阵,为下次递推做准备。
至此,卡尔曼滤波的理论推导到此结束。还有一些如实际应用中状态方程建立不正确,预测结果会怎样等这样的细节问题,以及一些总结留到第二部分讨论。
(转载请注明作者和出处:http://blog.csdn.net/heyijia0327 未经允许请勿用于商业用途)
reference:
1.Greg Welch & Gary Bishop. << An Introduction to the Kalman Filter >>
2.Tony Lacey. << Tutorial:The Kalman Filter >>.
3.Ramsey Faragher. << Understanding the Basis of the Kalman Filter Via a Simple and Intuitive Derivation >>
4.highgear . 《授之以渔:卡尔曼滤波器...大泄蜜...》
5.很多概念定义来自维基百科
卡尔曼滤波 -- 从推导到应用(二)
这部分主要是通过对第一部分中提到的匀加速小车模型进行位移预测。
先来看看状态方程能建立准确的时候,状态方程见第一部分分割线以后内容,小车做匀加速运动的位移的预测仿真如下。
得到的仿真图像:
绿线为真实值,蓝色的为噪声很大的测量值,红线为估计值。由此可以看出卡尔曼滤波确实相当犀利,提供了一个顺滑的最优的估计。并请注意代码中,特地使得估计是从第9个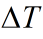
但这里请注意图像中画红圈部分,由于一开始你预测值为0,而实际上不是(它已经运动9个时间间隔了),所以估计出的效果不好。在这里回忆前面讨论过的K值大小和估计的关系,既然预测不准,那么一开始我就先相信测量呗。这就涉及估计值误差协方差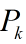
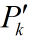
它又和估计误差协方差矩阵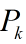
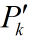
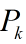
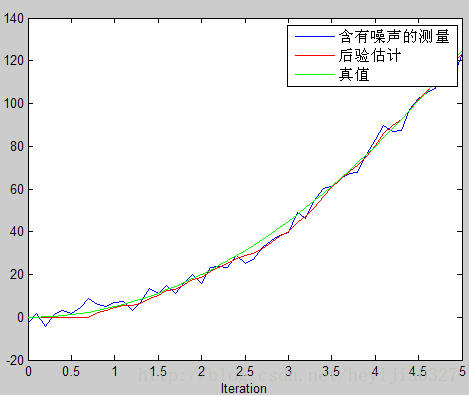
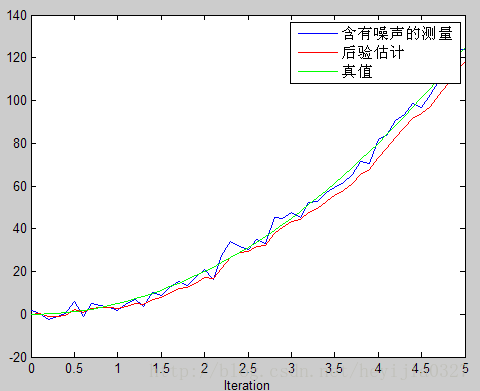
修改初值P=[2 0;0 2],估计图像如下,可以看到初始估计明显改进了。(两幅图中,测量值相同,只改变了P)。这幅图中红色水平线那部分是前9个时间段,你还没开始雷达追踪,所以是水平的为0。
好了,到第二个问题,当状态方程建立不正确的又会怎样呢?实际应用中很多时候我们不能建立正确的状态方程。
我们假设建立的状态方程如下:
转换矩阵A,B,H都等于1.这个模型明显是不正确的。
注意这个时候的系统噪声,就不单单只是系统内部产生的,还包括你建立状态方程的不正确性。你建立的越不正确,根据你模型进行的预测就不正确,从这个角度来说,相当于你的噪声增大了。所以这个时候系统噪声W的方差应该增大。理解这一点,对改进实际估计效果有好处。接下来通过对比不同的W方差值设定给出对比,贴出这部分仿真如下。
最开始假设系统噪声方差和前面状态建立正确的时候一样为0.9,估计图像如图(a)。效果不理想,我们知道状态方程建立错误了,系统噪声方差应该比之前大。于是增大系统噪声方差再预测,如图(b)
图(a)
图(b)
两个图中测量值是一样的,只是第二图中将系统噪声方差Q增大到2。对比可以看出,特别是图像后半段,图(b)比图(a)效果更接近真实值。
至此,从推导到应用接近尾声了,但我在这里还有一个问题就是,你随便给的x的预测初值,模型建立也不正确,kalman filter 竟然依然这么犀利,那么他收敛性怎么证明呢?写这文章的时候,笔者没有看详细的数学证明,但是由前面说到的kalman filter和数值分析里递推求解方程组时用的Gauss-Seidel 迭代法,两者真的很相近,于是我直观的认为卡尔曼的收敛性和Gauss-Seidel 一样。Gauss-Seidel迭代法里权重的选取能使得递推收敛真实值,因此卡尔曼滤波里增益K的每次计算就是卡尔曼收敛的重要保证。
最后再说一句个人可能不正确观点,抛砖迎玉,卡尔曼滤波最后收敛得到的方程就是维纳滤波,卡尔曼滤波是一步一步递推然后收敛到真实值,维纳滤波是直接计算出估计值,不是一步一步的结果,但两者都是最小均方差的思想在里面。因此,我在学卡尔曼的时候,想到数字图像里的维纳滤波,直观的想到,维纳滤波能做到的,卡尔曼应该也能做到。但这我也没去验证,倒是确实有这方面的论文。


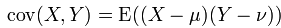
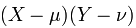
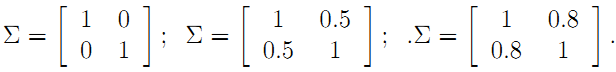
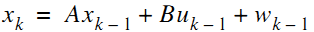
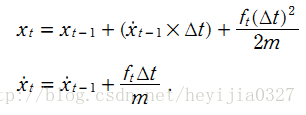

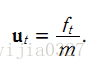
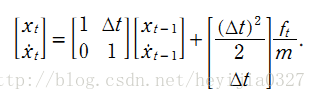
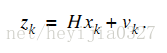
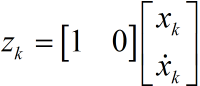
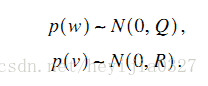
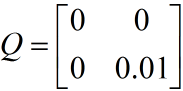
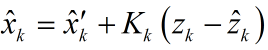
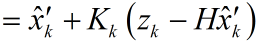
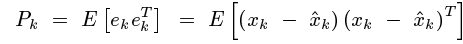
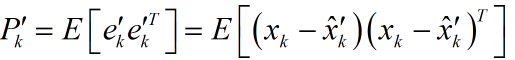
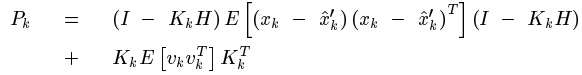
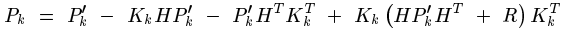
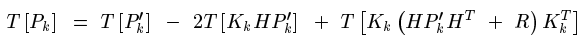
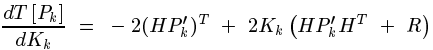
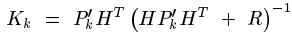
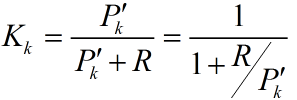
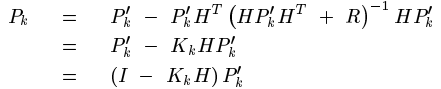
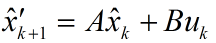
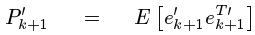
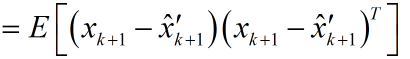
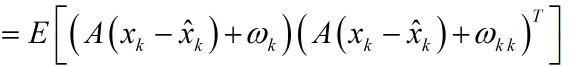
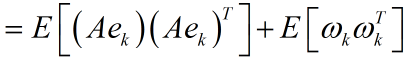
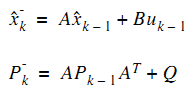
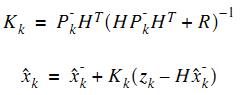
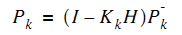
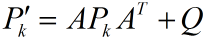
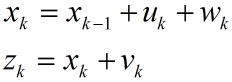


 浙公网安备 33010602011771号
浙公网安备 33010602011771号