【刷题记录】BZOJ2154 crash的数字表格 莫比乌斯反演
治好了我多年的公式恐惧症
https://www.luogu.org/problemnew/show/P1829
(放洛谷题号的原因是BZOJ上很多内容是限制级的(雾))
题目大意:已知M,N,求
(我采用数论教材上的方法表示最大公因数,即(i,j)表示i,j的最大公约数)
那么,我们开始吧。
不妨设n<m
令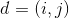
即
接下来是莫比乌斯函数的性质: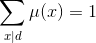
转化为枚举x
枚举t=dx
中间两个和式为等差数列求和,可以O(1)得到结果
经过完全归纳法证明,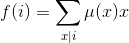
证明如下:
当i为质数时,显然
记p为任意质数
当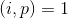
有
证完
接下来考虑线性筛的实现
考虑当
有
所以线性筛完成
依靠线性筛预处理后,可以O(n)时间预处理,再用O(n)时间得出结果
然而此题还可以再次优化
考虑到![[\frac nt]](https://img-blog.csdnimg.cn/20181223185105829)
![[\frac mt]](https://img-blog.csdnimg.cn/20181223185105919)
时间复杂度可以优化至O(n+sqrt(n))
这样可以解决多组数据的情况
代码
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cstring>
using namespace std;
int n,m;
#define ll long long
#define mod 20101009
#define inv2 10050505
#define N 10000000
int prime[N+9],mu[N+9];
bool notprime[N+8];
ll sum(int x)
{
return (((((ll)x*(x+1))%mod)*inv2)%mod);
}
int main()
{
scanf("%d%d",&n,&m);
if(n>m)swap(n,m);
notprime[1]=mu[1]=1;int tot = 0;
for(int i = 2; i <= n; i ++)
{
if(!notprime[i])
{
prime[++tot]=i;
mu[i]=(1-i+mod)%mod;
}
for(int j = 1; j <= tot &&prime[j]*i<=n; j ++)
{
notprime[prime[j]*i]=1;
if(i%prime[j]==0)
{
mu[i*prime[j]]=mu[i];
break;
}
else
{
mu[i*prime[j]]=(((ll)mu[i]*(1-prime[j])%mod)+mod)%mod;
}
}
mu[i]=((((ll)i*mu[i])%mod+mu[i-1])%mod+mod)%mod;
}
int ans = 0;
for(int i = 1,last; i <= n; i =last +1)
{
last = min(n/(n/i),m/(m/i));
ans = (((((sum(n/i)*sum(m/i))%mod)*(mu[last]-mu[i-1]))%mod+mod)%mod+ans)%mod;
}
printf("%d",ans);
}


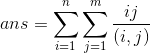
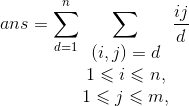
![ans = \sum _{d=1}^{n} d\sum_{(i,j)=1}^{1\leq i\leq [\frac nd],1\leq j\leq [\frac md]}{ij}](https://img-blog.csdnimg.cn/20181223185105655)
![ans = \sum _{d=1}^{n} d\sum_{i=1}^{[\frac nd]}\sum_{j=1}^{[\frac md]}\sum_{x|(i,j)}\mu (x){ij}](https://img-blog.csdnimg.cn/20181223185105686)
![ans = \sum_{d=1}^{ n}d\sum_{x=1}^{[\frac nd]}\mu(x)x^2\sum_{j=1}^{[\frac n {dx}]}\sum_{i=1}^{[\frac m {dx}]}ij](https://img-blog.csdnimg.cn/20181223185105700)
![ans = \sum_{t=1}^{ n}t\sum_{i=1}^{[\frac nt]}\sum_{j=1}^{[\frac mt]}ij\sum_{x|t}\mu(x)x=\sum_{t=1}^{ n}t(\sum_{i=1}^{[\frac nt]}i)(\sum_{j=1}^{[\frac mt]}j)\sum_{x|t}\mu(x)x](https://img-blog.csdnimg.cn/20181223185105720)
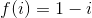
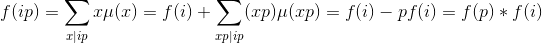
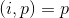
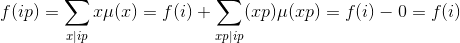

 浙公网安备 33010602011771号
浙公网安备 33010602011771号