浅谈树上分治算法[国集2019]
1.点分治 && 边分治
这两种算法都是用于处理这样一类问题:
给定一棵树,求有多少条路径满足xxx性质?/ 最xxx的路径是什么?
例题:给定一棵树,求有多少条路径长度小于等于k?
使用点/边分治就可以将暴力枚举两点的\(O(n^2)\)优化到\(O(n\log n)\)
点分治
我们改一下这道题 改成求有多少条经过1的路径长度小于等于k
这个就比较好求了 我们把所有点到1的距离全部装进一个数组\(q\)里,然后只需要计算\(q\)数组里有多少对数字相加小于等于即可,这个可以排序后维护双指针计算
但是这样做是错的。。。
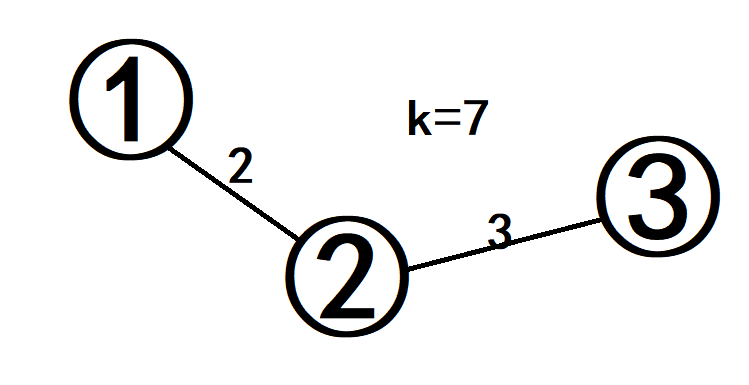
\(q\)数组里有\(0,2,5\),那么\(0+2,0+5,2+5\)都小于等于\(k\),求得答案有三个,但是实际上合法的经过\(1\)的路径只有\(1\)到\(2\),\(1\)到\(3\)两条
我们注意到\(2+5\)是不合法的 你不能这么走:2->1->3 所以只有 不在\(1\)的同一个儿子的子树中 的两个点才能相加配对
怎么处理?也很简单 按上面的方法计算完后 显然是有些不合法的情况 于是再用同样的方法计算\(1\)的每一个儿子的子树 把儿子的子树里的所有点进行配对 这些配对都是不合法的 减去这些配对的贡献即可
然后看点分治
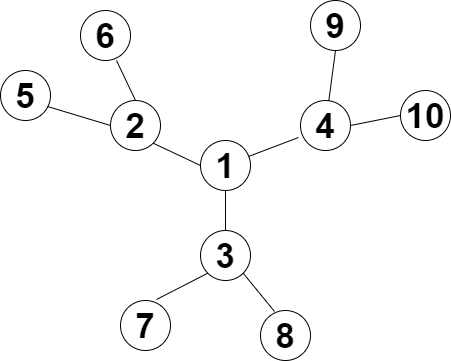
看这个分叉的菊花图 找到它的重心是\(1\)
我们可以用上面的方法计算出有多少经过1的路径长度小于等于k,然后我们删除点1
现在图上还剩下三棵子树 再如法炮制分别找到这三棵子树的重心,然后分别统计过这三个重心的合法路径条数,然后再分别删除这三个重心......
树的重心有个性质:它每个儿子的子树大小都不会超过\(\frac{n}{2}\)
所以最多会往下递归\(\log n\)层,此题的总复杂度\(O(n\log^2 n)\)
核心步骤:找到当前子树重心 -> 统计经过重心的路径的贡献 -> 删除重心,递归进入子树
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
inline int read() {
int x = 0, f = 1; char ch = getchar();
for (; ch > '9' || ch < '0'; ch = getchar()) if (ch == '-') f = -1;
for (; ch <= '9' && ch >= '0'; ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ '0');
return x * f;
}
const int inf = 0x7fffffff;
int n, k, rt, nowsz, mx;
int head[40005], pre[80005], to[80005], val[80005], sz;
int siz[40005], dis[40005];
ll ans;
bool vis[40005];
void init() {
memset(head, 0, sizeof(head));
memset(vis, 0, sizeof(vis));
sz = 0; ans = 0;
}
inline void addedge(int u, int v, int w) {
pre[++sz] = head[u]; head[u] = sz; to[sz] = v; val[sz] = w;
pre[++sz] = head[v]; head[v] = sz; to[sz] = u; val[sz] = w;
}
void getsiz(int x, int fa) {
siz[x] = 1;
for (int i = head[x]; i; i = pre[i]) {
int y = to[i];
if (y == fa || vis[y]) continue;
getsiz(y, x);
siz[x] += siz[y];
}
}
void getrt(int x, int fa, int tot) {
int nowmx = 0;
for (int i = head[x]; i; i = pre[i]) {
int y = to[i];
if (y == fa || vis[y]) continue;
getrt(y, x, tot);
nowmx = max(nowmx, siz[y]);
}
nowmx = max(nowmx, tot - siz[x]);
if (nowmx < mx) {
mx = nowmx, rt = x;
}
}
int l, r, q[40005];
void getdis(int x, int fa) {
q[++r] = dis[x];
for (int i = head[x]; i; i = pre[i]) {
int y = to[i];
if (y == fa || vis[y]) continue;
dis[y] = dis[x] + val[i];
getdis(y, x);
}
}
ll calc(int x, int d) {
l = 1, r = 0;
dis[x] = d;
getdis(x, 0);
sort(q + 1, q + r + 1);
ll ret = 0;
while (l < r) {
if (q[l] + q[r] <= k) {
ret += r - l, l++;
} else r--;
}
return ret;
}
void divide(int x) {
ans += calc(x, 0);
vis[x] = 1;
getsiz(x, 0);
for (int i = head[x]; i; i = pre[i]) {
int y = to[i];
if (vis[y]) continue;
ans -= calc(y, val[i]);
mx = inf;
getrt(y, 0, siz[y]);
divide(rt);
}
}
int main() {
n = read();
init();
for (int i = 1; i < n; i++) {
int u = read(), v = read(), w = read();
addedge(u, v, w);
}
k = read();
mx = inf;
getsiz(1, 0);
getrt(1, 0, n);
divide(rt);
printf("%lld\n", ans);
return 0;
}
边分治
上面那道题还有第二种做法,即边分治
点分治是每次选出中间的重心点,边分治则是选出一条比较靠近中间的边,使得这条边连接的两棵子树中,较大的那棵子树尽可能小
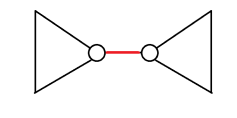
然后统计完所有经过这条边的路径后把这条边删除,再递归进入左右两棵子树
这里统计贡献时就不用向上面一样去重了,因为一定是把这条边左边的点和右边的点进行配对,就不存在不合法的情况
时间复杂度是和点的度数有关的 当度数均为常数时,时间复杂度约为\(O(n\log n)\)
菊花图怎么办?这里有一个优化 我们想让每个点的度数尽可能小,可以通过新加入一些点和边来减小每个点的度数
具体地说,如果一个点\(x\)有多于两个儿子,我们就新建两个点\(a,b\),把这两个点的父亲都设为\(x\),然后把\(x\)的儿子一半给\(a\),一半给\(b\)
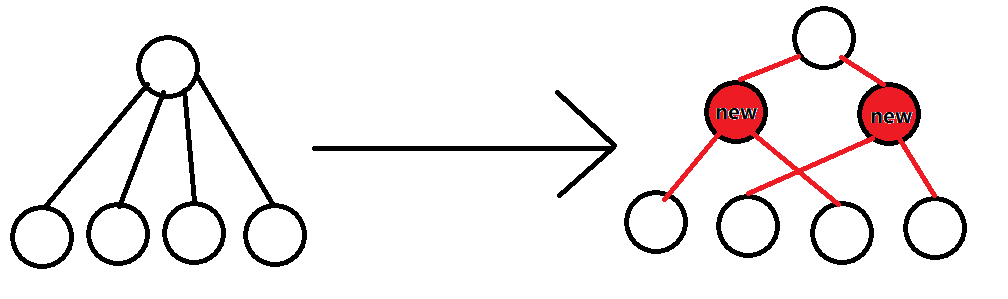
如果此时\(a,b\)的儿子多于两个了,过一会还可以在\(a,b\)的下面继续建虚点
这样实际上最后会得到一棵二叉树 总点数依然是\(2n\)左右的 不过每个点的度数都不会超过3
统计答案时要注意虚点不能被计入答案
int siz[400005], ct, mx, sum;
void findct(int x, int fa) {
siz[x] = 1;
for (int i = head[x]; i; i = pre[i]) {
int y = to[i];
if (y == fa || vis[i>>1]) continue;
findct(y, x);
siz[x] += siz[y];
int now = max(siz[y], sum - siz[y]);
if (now < mx) {
mx = now;
ct = i;
}
}
}
int q[2][400005], top[2];
void getdis(int x, int fa, int dis, int o) {
if (x <= nn) q[o][++top[o]] = dis;
for (int i = head[x]; i; i = pre[i]) {
int y = to[i];
if (y == fa || vis[i>>1]) continue;
getdis(y, x, dis + val[i], o);
}
}
ll calc(int v) {
sort(q[0] + 1, q[0] + top[0] + 1);
sort(q[1] + 1, q[1] + top[1] + 1);
int l = 1, r = top[1];
ll ret = 0;
while (l <= top[0] && r >= 1) {
if (q[0][l] + q[1][r] + v <= k) {
ret += r;
l++;
} else r--;
}
return ret;
}
void divide(int x, int _siz) {
ct = 0, mx = 0x7fffffff, sum = _siz;
findct(x, 0);
if (!ct) return;
int l = to[ct], r = to[ct^1];
vis[ct>>1] = 1;
top[0] = top[1] = 0;
getdis(l, 0, 0, 0); getdis(r, 0, 0, 1);
ans += calc(val[ct]);
divide(l, siz[to[ct]]); divide(r, _siz - siz[to[ct]]);
}
例题1:[CTSC2018]暴力写挂
边分治的例题
注意到题目给的这个
似乎不太好算
我们把前3项转换一下 发现上面这个式子实际上等于
这样一来,前三项可以通过边分治处理出来,然后最后一项则需要在第二棵树上来计算
具体地说,我们对第一棵树进行边分治,然后将当前分治边左边的点标为黑点,右边标为白点
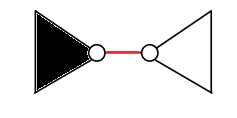
假设一个点\(x\)到分治边的距离为\(\mathrm{d}(x)\),分治边的长度是\(v\),那么上面式子的前3项实际上就等于\(\mathrm{depth}(x) + \mathrm{depth}(y) + (\mathrm{d}(x) + \mathrm{d}(y) + v)\)
所以把每个点的点权\(\mathrm{val}(x)\)设为\(\mathrm{depth}(x) + \mathrm{d}(x)\),然后就可以去处理第二棵树了
在第二棵树中枚举每个点作为lca,那么现在目标就是找到两个颜色不同,且在两个不同儿子子树里的点使得它们的\(\mathrm{val}\)之和最大
设\(f[x][0]\)表示\(x\)子树中最大的黑点权值,\(f[x][1]\)表示最大白点权值;然后就可以在第二棵树上进行dp来得到最大值 具体dp转移见代码
但是dp一次是\(O(n)\)的 所以我们还需要在dp之前对第二棵树建虚树 在虚树上dp
这样总时间复杂度就是\(O(n\log^2 n)\)的 依然会被卡掉。。。
如果想要\(O(n\log n)\)可以加上欧拉序+ST表求LCA以及基数排序建虚树来强行降低复杂度 这里我只写了个\(O(1)\)求LCA 吸氧后勉强卡过 基数排序什么的表示不懂
代码实在太长太长了。。。所以放个链接吧 https://www.luogu.com.cn/paste/4qxuvhi5
思考题:给定两个树,找出两个点x,y,使得第一棵树上x,y的距离和第二棵树上x,y的距离之和最小
没有找到原题 所以自己造了一下数据
首先进行点分治,然后对于一个分治中心,考虑所有包含它的连通块
我们先以分治中心为根,处理出当前子树的dfs序;
然后再进行dfs,对于一个非根的点 \(x\) 有两种选择:
-
将 \(x\) 加入连通块,在新图中从
dfn[x]向dfn[x]+1连边权为 \(v_x\) 的边 -
连通块中不包含 \(x\) 的子树,在新图中从
dfn[x]向ed[x]+1连边权为 \(0\) 的边
如果一条边的终点超过当前的总dfs序了,就把这条边连向汇点
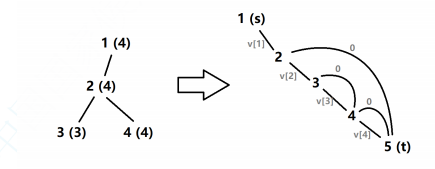
然后这样做一定能建出若干个这样的图 建立超级源点向每个源点连边权为 \(0\) 的边,建立超级汇点,从每个汇点向超级汇点连边
此时这个新图应该是一个有 \(n\log n\) 个点和 \(n\log n\) 条边的图,其中每条从超级源点到超级汇点的路径都代表原树的一个连通块
最后在这张新图上跑k短路求出答案
#include <bits/stdc++.h>
#define N 100005
#define M 2000005
using namespace std;
template<typename T>
inline void read(T &num) {
T x = 0, f = 1; char ch = getchar();
for (; ch > '9' || ch < '0'; ch = getchar()) if (ch == '-') f = -1;
for (; ch <= '9' && ch >= '0'; ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ '0');
num = x * f;
}
const int inf = 0x3f3f3f3f;
int n, k, a[N], siz[N], mn, rt;
int head[M], pre[M<<1], to[M<<1], val[M<<1], sz;
int head2[M], pre2[M<<1], to2[M<<1], val2[M<<1], sz2;
vector<int> e[N];
bool vis[M];
inline void addedge(int u, int v, int w) {
pre[++sz] = head[u]; head[u] = sz; to[sz] = v; val[sz] = w;
}
inline void addedge2(int u, int v, int w) {
pre2[++sz2] = head2[u]; head2[u] = sz2; to2[sz2] = v; val2[sz2] = w;
}
void getsiz(int x, int fa) {
siz[x] = 1;
for (auto y : e[x]) {
if (y == fa || vis[y]) continue;
getsiz(y, x);
siz[x] += siz[y];
}
}
void getrt(int x, int fa, int S) {
int now = 0;
for (auto y : e[x]) {
if (y == fa || vis[y]) continue;
getrt(y, x, S);
now = max(now, siz[y]);
}
now = max(now, S - siz[x]);
if (now < mn) {
mn = now;
rt = x;
}
}
int st[N], ed[N], rnk[M], tme = 1, s = 0, t = 1;
void calc(int x, int fa) {
st[x] = ++tme; rnk[tme] = x;
for (auto y : e[x]) {
if (y == fa || vis[y]) continue;
calc(y, x);
}
ed[x] = tme;
}
void calc2(int x, int fa, int R) {
if (x != R) {
addedge(st[x], ed[x] + 1 > tme ? t : ed[x] + 1, 0);
addedge2(ed[x] + 1 > tme ? t : ed[x] + 1, st[x], 0);
}
addedge(st[x], st[x] + 1 > tme ? t : st[x] + 1, a[x]);
addedge2(st[x] + 1 > tme ? t : st[x] + 1, st[x], a[x]);
for (auto y : e[x]) {
if (y == fa || vis[y]) continue;
calc2(y, x, R);
}
}
void divide(int x) {
calc(x, 0);
calc2(x, 0, x);
addedge(s, st[x], 0);
addedge2(st[x], s, 0);
getsiz(x, 0);
vis[x] = 1;
for (auto y : e[x]) {
if (vis[y]) continue;
mn = inf;
getrt(y, 0, siz[y]);
divide(rt);
}
}
int h[M];
priority_queue<pair<int, int> > qq;
void dijkstra() {
memset(vis, 0, sizeof(vis));
memset(h, 0x3f, sizeof(h));
qq.push(make_pair(0, 1));
h[1] = 0;
while (!qq.empty()) {
int x = qq.top().second; qq.pop();
if (vis[x]) continue;
vis[x] = 1;
for (int i = head2[x]; i; i = pre2[i]) {
int y = to2[i];
if (h[y] > h[x] + val2[i]) {
h[y] = h[x] + val2[i];
qq.push(make_pair(-h[y], y));
}
}
}
}
struct node{
int x, f, g;
node(int xx = 0, int ff = 0, int gg = 0): x(xx), f(ff), g(gg) {}
bool operator < (const node b) const {
return f > b.f;
}
};
priority_queue<node> q;
int cnt[M];
int A_star() {
q.push(node(0, 0, 0));
while (!q.empty()) {
node now = q.top(); q.pop();
int x = now.x; cnt[x]++;
if (x == 1 && cnt[x] == k) {
return now.f;
}
if (cnt[x] > k) continue;
for (int i = head[x]; i; i = pre[i]) {
int y = to[i];
q.push(node(y, now.g + val[i] + h[y], now.g + val[i]));
}
}
}
int main() {
read(n); read(k);
for (int i = 1; i <= n; i++) read(a[i]);
for (int i = 1, u, v; i < n; i++) {
read(u); read(v);
e[u].push_back(v); e[v].push_back(u);
}
mn = inf;
getsiz(1, 0);
getrt(1, 0, n);
divide(rt);
dijkstra();
printf("%d\n", A_star());
return 0;
}
2. 全局平衡二叉树
一般在这样一些问题里可以用于优化LCT:树的结构不会发生变化(加边或删边),询问整颗树或子树的答案(询问路径好像也可以做,但是很难写,不如用LCT)
由此可见,这个"全局平衡二叉树"的可应用区间是很小的
不过对于一些动态DP问题,显然是满足上面的两个可应用条件的,这时候它的优势就显现出来了:
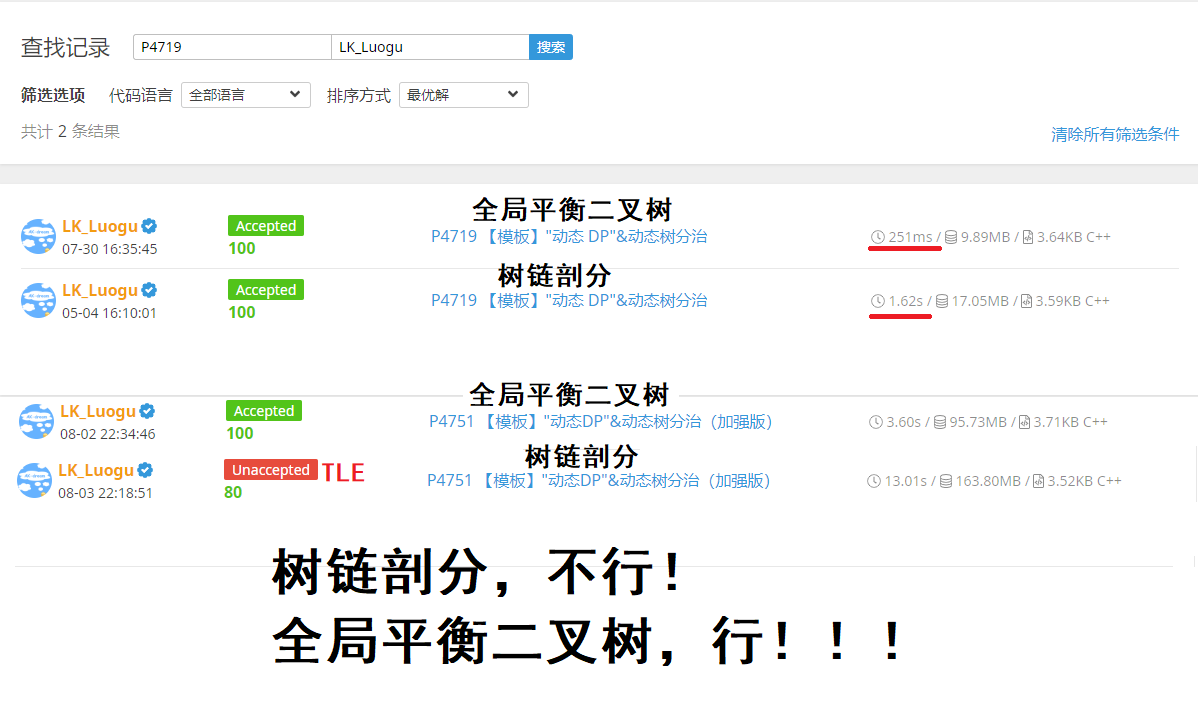
例题一 Luogu P4751
动态DP的模板题 使用大众写法树链剖分时间复杂度为 \(O(n\log^2 n)\)
使用LCT虽然时间复杂度为 \(O(n\log n)\),但是常数较大
注意到每次询问都是询问根节点信息,而且树的形态不会改变,所以可以用全局平衡二叉树,时间复杂度 \(O(n\log n)\),常数小,行!
全局平衡二叉树在解决动态DP问题时与LCT和树剖各有相似之处:
和树剖一样,都是将轻儿子和重链的信息分开维护(LCT是不是也是啊),然后在重链上合并
和LCT一样,建出来的新树也是由若干棵二叉树通过轻边相连,每棵二叉树代表一条重链
和LCT不一样的地方则是:全局平衡二叉树不再需要Splay那样的旋转 而是一棵静态的树
既然它是静态的 那我们自然希望它的高度越小越好 所以建树时我们就希望把它的高度控制在 \(\log n\) 左右
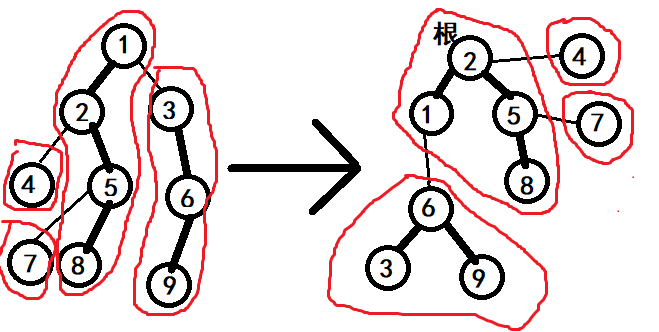
这是一棵树对应的全局平衡二叉树的例子 粗边代表重边 可以发现它和LCT长得很像
如何建树?我们设 \(siz[x]\) 表示 \(x\) 的子树大小,\(son[x]\) 为 \(x\) 的重儿子
设 \(lsiz[x]=siz[x]-siz[son[x]]\) 表示 \(x\) 和它所有轻子树的大小之和,令 \(lsiz[x]\) 为每个点的点权
那么对于每条重链对应的二叉树,我们找出这段重链中的一个点,使得它左边的点权和与它右边的点权和之间的差距较小,把它作为二叉树的根,然后向左右儿子递归
可以证明,这样建出的全局平衡二叉树树高是 \(\log n\) 的
建树代码如下:
int build2(int l, int r) {
if (l > r) return 0;
int sum = 0;
for (int i = l; i <= r; i++) sum += lsiz[stk[i]];
for (int i = l, now = lsiz[stk[l]]; i <= r; i++, now += lsiz[stk[i]]) {
//将每个点的点权设为lsiz[x],找到位于中间的点,作为当前二叉树的根
if (now * 2 >= sum) {
int lc = build2(l, i - 1), rc = build2(i + 1, r); //递归建出左右儿子
ch[stk[i]][0] = lc; ch[stk[i]][1] = rc;
fa[lc] = fa[rc] = stk[i];
pushup(stk[i]); //pushup在后面讲
return stk[i];
}
}
}
int build(int x) { //建出x的全局平衡二叉树 (x是一条重链的开头)
for (int y = x; y; y = son[y]) {
vis[y] = 1; //将当前重链上的点打上标记
}
for (int y = x; y; y = son[y]) {
for (int i = head[y]; i; i = pre[i]) {
int z = to[i]; //遍历每个和当前重链上任意一点相连的轻儿子
if (!vis[z]) { //z为轻儿子,一定是另外一条重链的开头
int rtz = build(z);
fa[rtz] = y;
//将下面那棵树的根节点的父亲设为y
}
}
}
top = 0;
for (int y = x; y; y = son[y]) {
stk[++top] = y; //提取出以x开头的重链
}
int ret = build2(1, top); //建出这棵重链的二叉树
return ret;
}
众所周知,动态DP是用矩阵乘法来维护的,这里我们一样通过矩阵乘法来维护DP值
这道题具体的转移矩阵就不写了,可以自行去看题解
类似LCT维护子树信息的思路,我们对每个点维护两个矩阵 \(now\) 和 \(now2\)
其中 \(now\) 存储的是自己和所有轻子树的信息,而 \(now2\) 则是 \(now\) 乘上左右儿子的信息
pushup操作:
inline void pushup(int x) {
now2[x] = now[x];
if (ch[x][0]) {
now2[x] = now2[ch[x][0]] * now2[x];
}
if (ch[x][1]) {
now2[x] = now2[x] * now2[ch[x][1]];
}
}
每次进行修改操作x v时,先修改 \(x\) 的 \(now\) 矩阵中对应的信息,然后暴力向上跳父亲
如果父亲连向自己的边是重边,就可以直接pushup,否则是轻边,需要修改父亲的 \(now\) 矩阵信息
修改也很简单 先将 \(fa[x]\) 的矩阵减去原先 \(x\) 的贡献,再加上 \(x\) 修改后的贡献即可
以此题为例:
void update(int x, int v) {
now[x].m[1][0] += v - a[x];
a[x] = v;
for (int y = x; y; y = fa[y]) {
if (fa[y] && ch[fa[y]][0] != y && ch[fa[y]][1] != y) { //轻边
now[fa[y]].m[0][0] -= max(now2[y].m[0][0], now2[y].m[1][0]);
now[fa[y]].m[0][1] = now[fa[y]].m[0][0];
now[fa[y]].m[1][0] -= now2[y].m[0][0];
//减去旧的信息
pushup(y);
now[fa[y]].m[0][0] += max(now2[y].m[0][0], now2[y].m[1][0]);
now[fa[y]].m[0][1] = now[fa[y]].m[0][0];
now[fa[y]].m[1][0] += now2[y].m[0][0];
//加上新的信息
} else pushup(y); //重边
}
}
修改完后,根节点的 \(now2\) 矩阵就是最终答案
由于全局平衡二叉树的树高是 \(\log n\) 的,所以一次修改操作的时间复杂度即为 \(O(\log n)\)
主要的难点在于如何建树,修改操作与树剖及LCT区别不大
只要学会建树,代码难度其实远小于树剖或LCT
#include <bits/stdc++.h>
#define N 100005
using namespace std;
template<typename T>
inline void read(T &num) {
T x = 0, f = 1; char ch = getchar();
for (; ch > '9' || ch < '0'; ch = getchar()) if (ch == '-') f = -1;
for (; ch <= '9' && ch >= '0'; ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ '0');
num = x * f;
}
int n, m, rt, a[N], head[N], pre[N<<1], to[N<<1], sz;
int siz[N], lsiz[N], son[N], fa[N], ch[N][2];
int f[N][2], g[N][2];
struct matrix{
int m[2][2];
matrix() {
m[0][0] = m[1][1] = m[0][1] = m[1][0] = 0;
}
matrix operator * (const matrix b) const {
matrix c;
c.m[0][0] = max(m[0][0] + b.m[0][0], m[0][1] + b.m[1][0]);
c.m[0][1] = max(m[0][0] + b.m[0][1], m[0][1] + b.m[1][1]);
c.m[1][0] = max(m[1][0] + b.m[0][0], m[1][1] + b.m[1][0]);
c.m[1][1] = max(m[1][0] + b.m[0][1], m[1][1] + b.m[1][1]);
return c;
}
} now[N], now2[N];
inline void addedge(int u, int v) {
pre[++sz] = head[u]; head[u] = sz; to[sz] = v;
pre[++sz] = head[v]; head[v] = sz; to[sz] = u;
}
void dfs(int x, int fa) {
siz[x] = 1;
for (int i = head[x]; i; i = pre[i]) {
int y = to[i];
if (y == fa) continue;
dfs(y, x);
siz[x] += siz[y];
if (!son[x] || siz[son[x]] < siz[y]) son[x] = y;
}
lsiz[x] = siz[x] - siz[son[x]];
}
void dfs2(int x, int fa) {
f[x][0] = g[x][0] = 0;
f[x][1] = g[x][1] = a[x];
if (son[x]) {
dfs2(son[x], x);
f[x][0] += max(f[son[x]][0], f[son[x]][1]);
f[x][1] += f[son[x]][0];
}
for (int i = head[x]; i; i = pre[i]) {
int y = to[i];
if (y == fa || y == son[x]) continue;
dfs2(y, x);
f[x][0] += max(f[y][0], f[y][1]);
f[x][1] += f[y][0];
g[x][0] += max(f[y][0], f[y][1]);
g[x][1] += f[y][0];
}
}
int stk[N], top;
bool vis[N];
inline void pushup(int x) {
now2[x] = now[x];
if (ch[x][0]) {
now2[x] = now2[ch[x][0]] * now2[x];
}
if (ch[x][1]) {
now2[x] = now2[x] * now2[ch[x][1]];
}
}
int build2(int l, int r) {
if (l > r) return 0;
int sum = 0;
for (int i = l; i <= r; i++) sum += lsiz[stk[i]];
for (int i = l, now = lsiz[stk[l]]; i <= r; i++, now += lsiz[stk[i]]) {
if (now * 2 >= sum) {
int lc = build2(l, i - 1), rc = build2(i + 1, r);
ch[stk[i]][0] = lc; ch[stk[i]][1] = rc;
fa[lc] = fa[rc] = stk[i];
pushup(stk[i]);
return stk[i];
}
}
}
int build(int x) {
for (int y = x; y; y = son[y]) {
vis[y] = 1;
}
for (int y = x; y; y = son[y]) {
for (int i = head[y]; i; i = pre[i]) {
int z = to[i];
if (!vis[z]) { //z为轻儿子
int rtz = build(z);
fa[rtz] = y;
}
}
}
top = 0;
for (int y = x; y; y = son[y]) {
stk[++top] = y;
}
int ret = build2(1, top);
return ret;
}
void update(int x, int v) {
now[x].m[1][0] += v - a[x];
a[x] = v;
for (int y = x; y; y = fa[y]) {
if (fa[y] && ch[fa[y]][0] != y && ch[fa[y]][1] != y) {
now[fa[y]].m[0][0] -= max(now2[y].m[0][0], now2[y].m[1][0]);
now[fa[y]].m[0][1] = now[fa[y]].m[0][0];
now[fa[y]].m[1][0] -= now2[y].m[0][0];
pushup(y);
now[fa[y]].m[0][0] += max(now2[y].m[0][0], now2[y].m[1][0]);
now[fa[y]].m[0][1] = now[fa[y]].m[0][0];
now[fa[y]].m[1][0] += now2[y].m[0][0];
} else pushup(y);
}
}
int main() {
read(n); read(m);
for (int i = 1; i <= n; i++) read(a[i]);
for (int i = 1, u, v; i < n; i++) {
read(u); read(v);
addedge(u, v);
}
dfs(1, 0); dfs2(1, 0);
for (int i = 1; i <= n; i++) {
now[i].m[0][0] = now[i].m[0][1] = g[i][0];
now[i].m[1][0] = g[i][1]; now[i].m[1][1] = -0x3f3f3f3f;
}
rt = build(1);
for (int i = 1, x, y; i <= m; i++) {
read(x); read(y);
update(x, y);
printf("%d\n", max(now2[rt].m[0][0], now2[rt].m[1][0]));
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号