数据结构(八)高级搜索树
AVL树是典型的适度平衡的二叉搜索树,为每个节点定义引入平衡因子的指标,平衡银子绝对值小于等于1,虽然和理想平衡相比,已经放松了限制,但条件仍显苛刻,还要在动态调整中保持这种特性。
一、伸展树
局部性
Locality:刚被访问的数据,极有可能很快地再次被访问,这一现象在信息处理过程中屡见不鲜。
BST就是这样的一个例子
BST:刚刚被访问过的节点,极有可能很快地再次被访问,下一将要访问的节点,极有可能就在刚被访问过节点的附近。

利用局部性,能否更快?
列表

将访问的元素放到列表前端
BST的顶部元素访问的效率更高
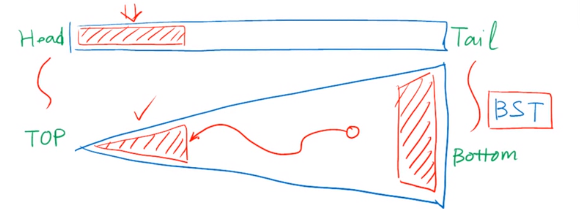
将经常访问的元素移送到更加靠近树根的位置,即降低深度
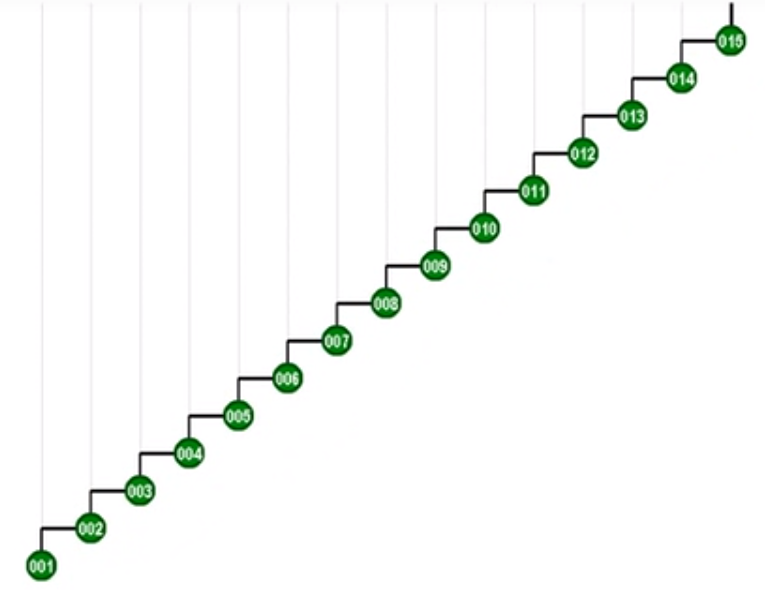
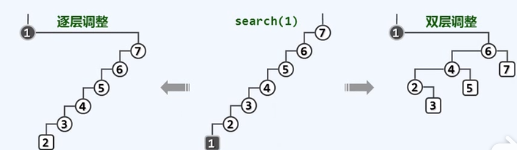
逐层伸展
节点v一旦被访问,随机被转移到树根
访问333
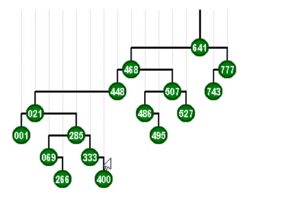

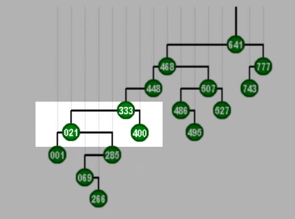
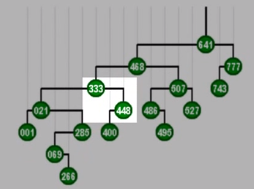


经过若干次zigzag的组合,最终到达了树根,对333的访问几乎只需要常数时间
该节点上升的过程是左右摇摆不断伸展的过程
一步一步往上爬
自上而下,逐层单旋

直到v最终被推送至树根
最坏的情况下效率不佳
双层伸展


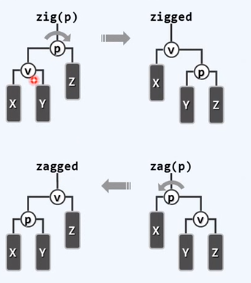
构思的精髓:向上追溯两层,而非一层
反复考察祖孙三代:g=parent(p), p=parent(v), v
根据它们的相对位置,经两次旋转使得v上升两层,成为(子)树根
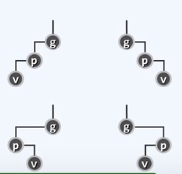
zig-zag/zag-zig
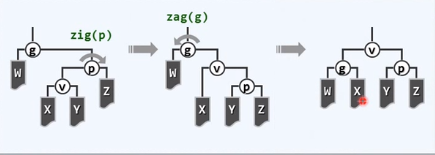
与AVL树双旋完全等效
与逐层伸展别无二致
zig-zig/zag-zag
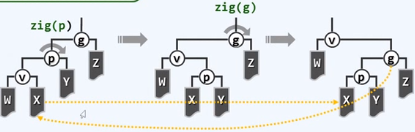
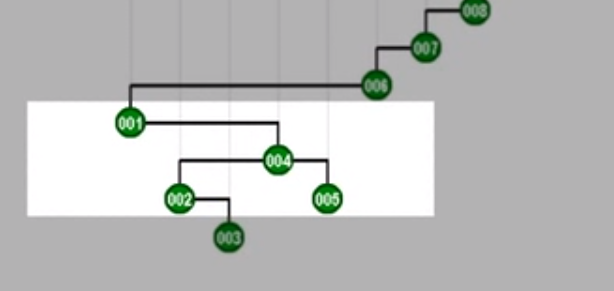
对祖父g进行zig
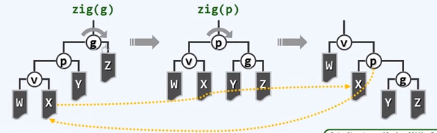
对祖父旋转

对父亲旋转
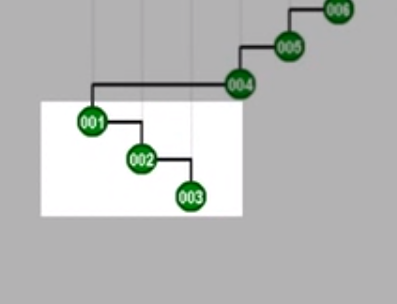
再对新祖父005zig旋转
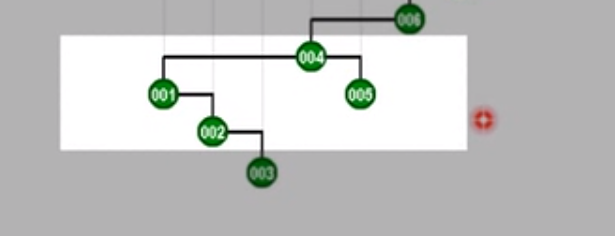
对父亲004zig旋转
继续上面的过程
最终
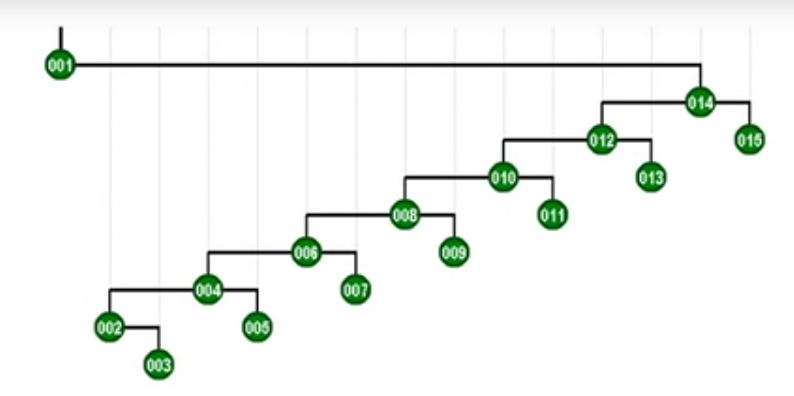
树的高度变为原来的一半
继续访问最低点,会继续优化调整
树的高度又缩减了一半
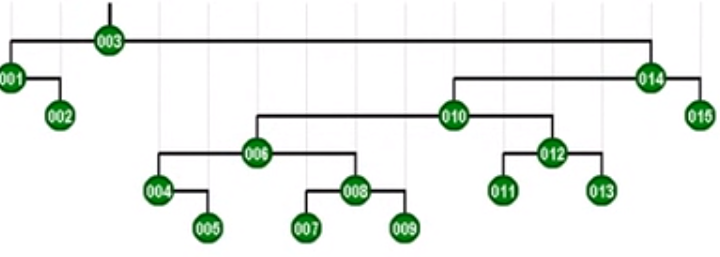
具有路径折叠效果
折叠效果:一旦访问坏节点,对应路径的长度将随即减半
最坏情况不致持续发生
单趟伸展操作,分摊O(logn)时间
实现


zig-zig情况

查找算法
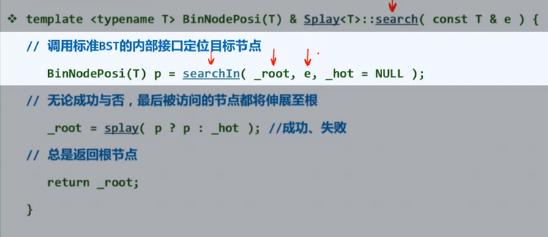
伸展树的查找操作,与常规BST::search()不同,很可能会改变树的拓扑结构,不再属于静态操作
插入算法
直观方法:调用BST标准的插入算法,再将新节点伸展至根,其中,首先需要调用BST::search()
重写后的splay::search()已集成了splay()操作,查找(失败)之后,_hot即是根节点

首先调用重写之后的search接口,不失一般性,查找是失败的,记失败之前最终的节点为t,即此前所说的_hot
集成在search接口内部的splay操作,自然会将_hot推送到树根的位置
在逻辑上将t这棵树一分为二,比如将t与其右子树分离开
引入节点v,并将t及其后代作为左子树,原先从t分离出的右子树作为树的右子树重写接入树中、
删除算法
直观方法:调用BST标准的删除算法,再将_hot伸展至根
同样的,Splay::search()查找(成功)之后,目标节点即是树根
既然如此,何不随即就在树根附近完成目标节点的摘除
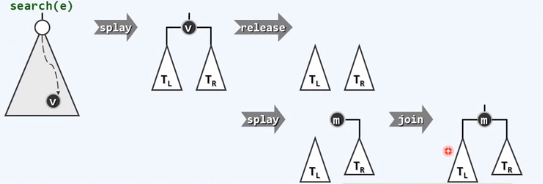
首先进行查找,对待删除的节点进行定位,定位成功v
紧随其后,集成在search接口内的伸展操作之后,待删除节点v被推送到树根
将该节点释放,从逻辑上,左右节点彼此分离
有很多方法重新合并它们,比如
在右子树中找到最小的节点,相对于左子树则是最大的
将原来的左子树作为左子树连接上去即可
二、B-树
严格讲,B-树并发BST,在物理上B-树的每个节点都可能包含多个分支,但逻辑上等价BST。
1.动机
高效I/O

越来越小的内存
事实上,系统存储容量的增长速度,远远小于问题规模的增长速度。

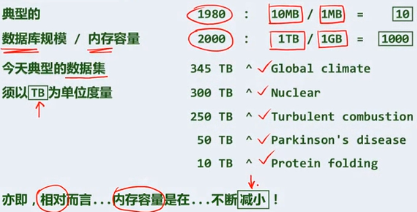
为什么不把内存做的更大?
物理上,存储器的容量越大/小,访问速度就越慢/快
高速缓存
事实1:不同容量的存储器,访问速度差异悬殊
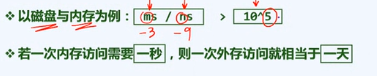
为避免1次外存访问,宁愿访问内存10次、100次,甚至更多
多数存储系统,都是分级组织的---Caching
最常用的数据尽可能放在更高层、更小的存储器中,实在找不到,才向更低层、更大的存储器索取

在该系统中,相对于任何一个存储级别,如果希望向更低的存储级别写入,或反过来从更低的存储级别读入数据,都称为输入和输出,简称I/O。
对于更上层的存储级别而言,对更低层的访问都可以叫做外存访问。
应尽可能减少I/O
事实2:从磁盘中读写1B,与读写1KB几乎一样快
批量式访问:以页(page)或快(block)为单位,使用缓冲区 // <stdio.h>...

B-Tree
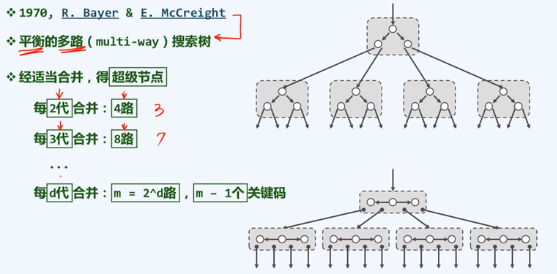

所谓m阶B-树,即m路平衡搜索树(m>=2)
外部节点的深度统一相等,等效于,所有叶节点的深度统一相等
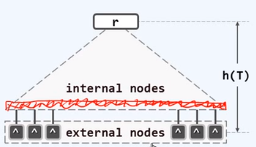
B-Tree的外部节点是叶节点数值为空,其实并不存在的孩子
与通常的BST不同,B-Tree的高度是相对于外部节点,而非叶子节点而言的
内部节点各有
不超过m-1个关键码:
不超过m个分支:
以n表示节点中所含的关键码数,因此拥有n个关键码的节点对应于n+1个分支
内部节点的分支数n+1也不能太少,具体的
树根:2<=n+1
其余: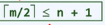
故亦称作![]()
m=5,称作(3, 5)-树
m=6,称作(3, 6)-树
(2, 4)树
紧凑表示
BTNode

3.B-树:查找
B树中容纳的词条极多,甚至不能完全容纳在内存中,相对的只能放在速度更慢的外存之中
B树查找的诀窍在于只载入必须的节点,尽可能减少I/O操作
对于一棵处于活跃状态的B树而言,不妨假设根节点已经常驻于内存
假设需要查找特定的关键字key
首先会在常驻于内存的根节点进行查找
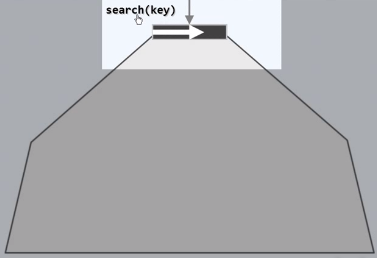
每个节点中的关键码都已经存成了一个向量,因此实施的无非是一个顺序查找,如果能在某个位置命中,查找随即以成功告终
查找失败于特定位置,在特定位置应该预先已经记录了引用,该引用将会指向B树中的下一层的某一个节点,可以沿着该引用找到下层的节点,并将其载入到内存之中
查找深入一层,代价是做了一次读入性的IO操作
既然已经搜索到这样一个节点,就可以断定,如果目标关键码的确存在这棵树中,就必然存在于这个节点所对应的子树中
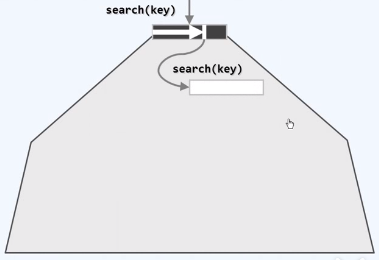
继续在新载入的节点中进行查找,只需顺序查找
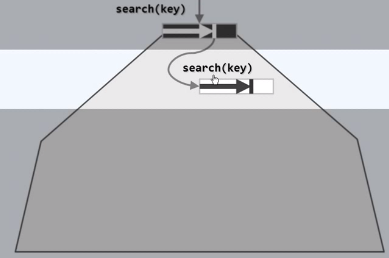
同样,如果查找以失败告终,此时,也会停止于某个位置,该位置预先记录了引用,可以据此找到B树的下一个节点
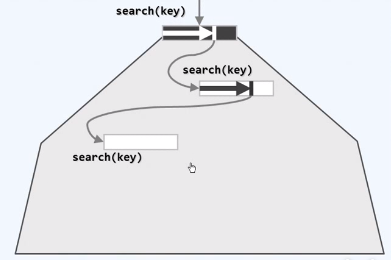
同样可以断定,如果目标关键码的确存在这棵B树中,就必然存在于这个节点所对应的子树中
因此,再次IO,将下层节点载入内存,在新载入的节点中做顺序查找

反复上述步骤,可能最终会到达叶节点

依然需要对目标关键码进行顺序查找,失败,会根据引用查找到下一层的节点,即外部节点

此时,会宣告查找以失败告终
当然,还有另一种情况,外部引用实际上指向的是相对而言更低层此的B树,借助外部节点可以将存放于不同级别上的B树串接起来,构成更大的B树
假设查找确实以失败告终
所谓B树查找不过是一系列在内存中顺序查找和一系列IO操作相间隔组成的操作序列
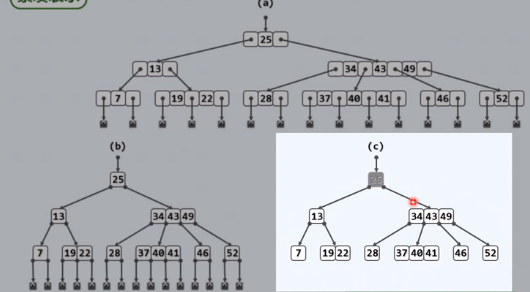
5阶B树,(3, 5)树

查找69,先查找内存中的根节点
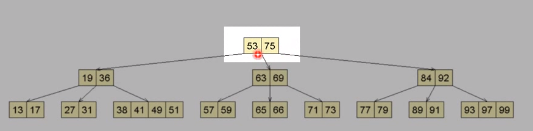
将下层的节点读入内存

在其中进行顺序查找,找到69
实现

复杂度
最大树高
含N个关键码的m阶B-树,最大高度=



最小树高


分裂
设上溢节点中的关键码依次为k0,...,km-1


关键码ks上升一层,并分裂split:以所得的两个节点作为左、右孩子
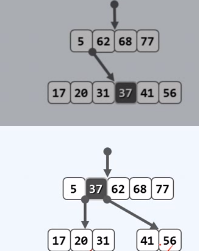
再分裂

插入555
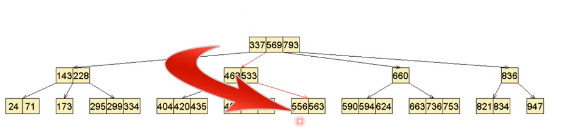
插入到紧邻556的左侧
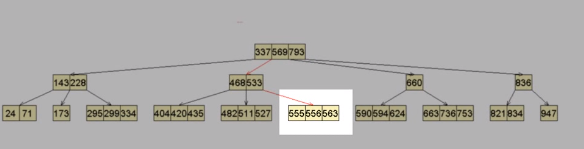
顺利结束
插入444

插到435的右侧

发生上溢
修复上溢,以中位数关键码为界,一分为二
中位数关键码提升一层,纳入到父节点的适当位置
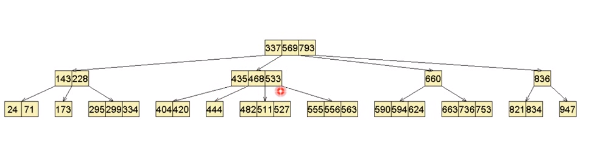
插入500

插入到482右侧
上溢
修复

仍上溢
再修复

再分裂
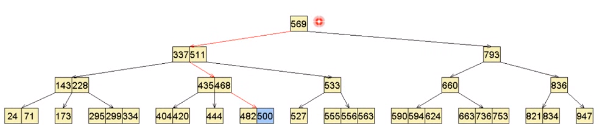
树长高了一层
5.B-树:删除
算法
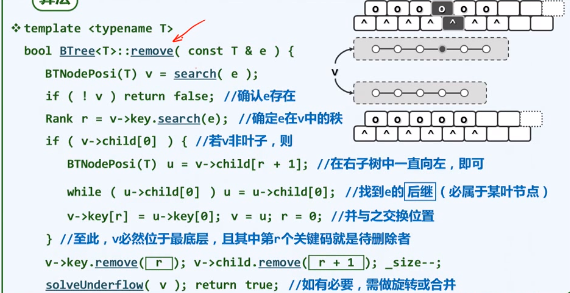
旋转

删除249
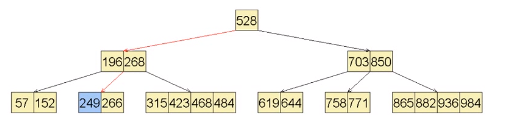
发生下溢
左顾右盼,有兄弟有四个关键码,可以借出一个
先向父亲借268,右兄弟给父亲315用来填补

删除619
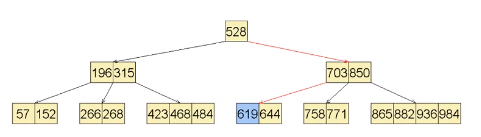
发生了下溢
左顾右盼,没有左兄弟,右兄弟没有足够的关键码
无法旋转,只能合并
从父节点中找到介于该节点和右兄弟的关键码,也就是703
取出下溢,作为粘合剂将该节点和右兄弟合并
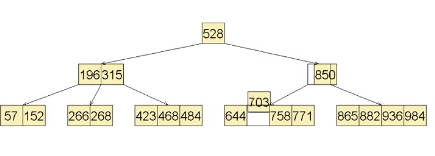
但是父亲发生了下溢
在父亲处左顾右盼,没有右兄弟,而左兄弟处于下溢的临界状态,无法借出关键码
合并
从父节点也就是树根中,找到下溢节点和兄弟之间的关键码
根节点只有一个关键码528
将该关键码取出并下溢,作为粘合剂将下溢节点和兄弟结合起来
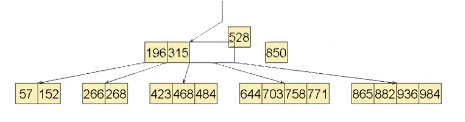
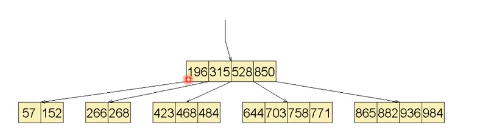
包含唯一节点的根节点成为空的,删除,用新的节点做根节点即可

B树高度降低了一层
三、红黑树
1.动机


这些结构每当经过一次动态操作,使得其中的逻辑结果发生变化后,会随机完全转入新的状态,同时将此前的状态完全遗忘,因此称作ephemeral structure

除了目标关键码,还要同时指定版本号ver
蛮力实现:每个版本独立保存,个版本入口自成一个搜索结构

空间上不可接受

利用相邻版本之间的关联性
O(1)重构
大量共享,少量更新:每个版本的新增复杂度,仅为O(logn)

为此,就树形结构的拓扑而言,相邻版本之间的差异不能超过O(1)
AVL树的删除操作不满足
需要一种BST:

红黑树是具有该特性的变种
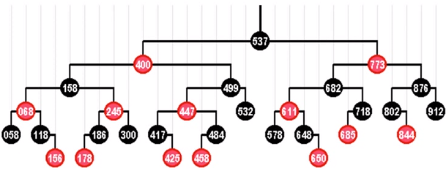

由红、黑两类节点组成的BST // 亦可给边染色
(统一增设外部节点NULL,使之成为真二叉树)
(1)树根:必为黑色
(2)外部节点:均为黑色
(3)其余节点:若为红,则只能有黑孩子 // 红之子、之父必黑
(4)外部节点到根:途中黑节点数目相等 // 黑深度
lifting变换
变换之前

变换之后

(2, 4)树==红黑树
提升各红节点,使之于其(黑)父亲等高--于是每棵红黑树,都对应于一棵(2, 4)-树
将黑节点与其红孩子视作(关键码并合并为)超级节点...
无法四种组合,分别对应于4阶B-树的一类内部节点 //反过来呢?
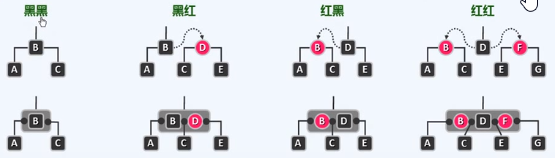
接口

3.红黑树:插入

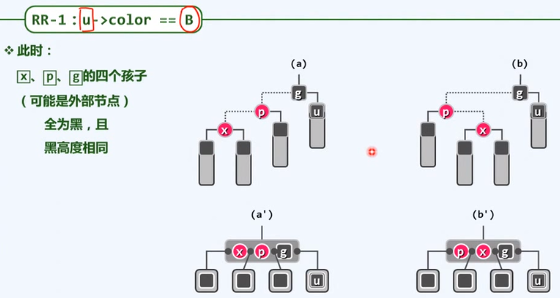
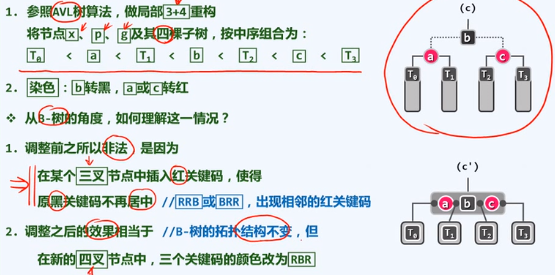
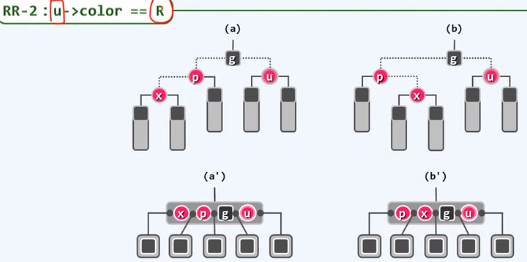
提升变换,所有指向红色节点的虚边收缩起来,从B树来看,局部的四个节点,合并为包含四个关键码的超级节点,对应于五个分支,非法的

红黑树中修复双红缺陷,不如说是在B树中修复上溢缺陷
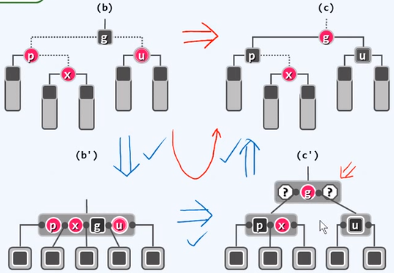
b -> b' -> c' -> c

g左右至少有一个黑色的关键码,也可能有红色,导致双红缺陷,根据上述方法再进行解决,问题所发生的位置会逐渐上升
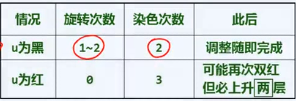
双红修正:复杂度
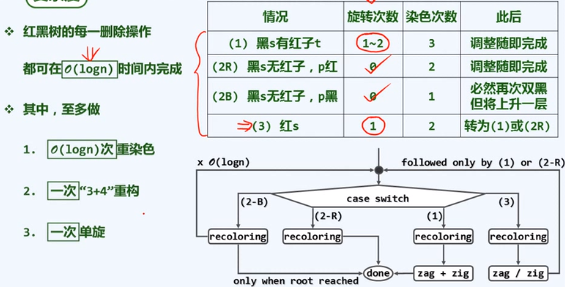
重构、染色均属常数时间的局部操作,故只需统计其总次数
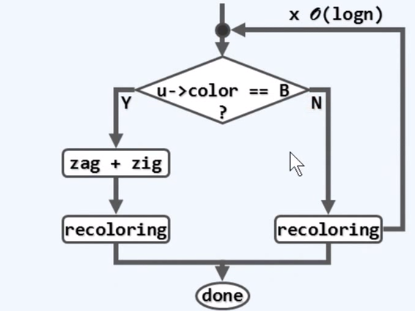
修正算法流程图

4.红黑树:删除
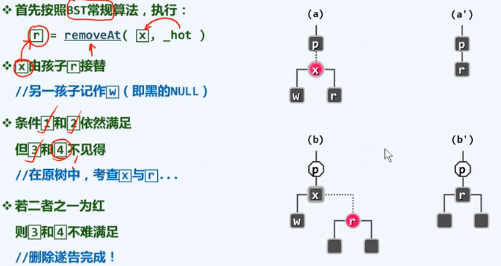
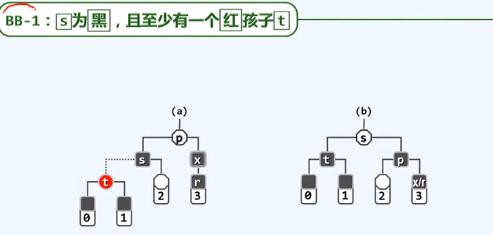

如此,红黑树性质在全局得以恢复--删除完成 //zig-zag等类似
在对应的B树中,以上操作等效于...


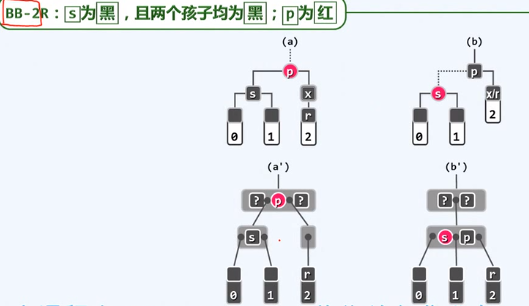




复杂度


 浙公网安备 33010602011771号
浙公网安备 33010602011771号