预备知识
1、矩阵运算
如果矩阵${{\mathop{\rm A}\nolimits} = {\left( {{a_{ij}}} \right)_{m \times n}}}$,其转置矩阵${{\mathop{\rm B}\nolimits} = {\left( {{b_{ji}}} \right)_{n \times m}} = {{\mathop{\rm A}\nolimits} ^T}}$的所有元素定义为
${{b_{ji}} = {a_{ij}}{,}\forall {1} \le i \le m{,1} \le j \le n}$
如果矩阵${{\mathop{\rm A}\nolimits} = {\left( {{a_{ij}}} \right)_{m \times n}}}$,其旋转${180^\circ }$为
${rot{\rm{ }}180\left( {\mathop{\rm A}\nolimits} \right) = {\left( {{a_{m - i + 1{,n - }j + 1}}} \right)_{m \times n}}}$
给定两个矩阵${{\mathop{\rm A}\nolimits} = {\left( {{a_{ij}}} \right)_{m \times n}}}$和${{\mathop{\rm B}\nolimits} = {\left( {{b_{ij}}} \right)_{n \times p}}}$,其乘积${{\mathop{\rm C}\nolimits} = {\left( {{c_{ij}}} \right)_{m \times p}} = {\mathop{\rm A}\nolimits} \cdot {\mathop{\rm B}\nolimits} = {\mathop{\rm A}\nolimits} {\mathop{\rm B}\nolimits} }$的所有元素定义为
${{c_{ij}}{\rm{ = }}\sum\limits_{k = 1}^n {{a_{ik}}{b_{kj}}} {,}\forall {1} \le i \le m{,1} \le j \le p}$
给定两个矩阵${{\mathop{\rm A}\nolimits} = {\left( {{a_{ij}}} \right)_{m \times n}}}$和${{\mathop{\rm B}\nolimits} = {\left( {{b_{ij}}} \right)_{m \times n}}}$,其加法和减法为
${{\mathop{\rm A}\nolimits} \pm {\mathop{\rm B}\nolimits} = {\left( {{a_{ij}} \pm {b_{ij}}} \right)_{m \times n}}}$
其阿达玛积(Hadamard product),又称为逐元素积定义为
${{\mathop{\rm A}\nolimits} \circ {\mathop{\rm B}\nolimits} = {\left( {{a_{ij}} \times {b_{ij}}} \right)_{m \times n}}}$
给定两个矩阵${{\mathop{\rm A}\nolimits} = {\left( {{a_{ij}}} \right)_{m \times n}}}$和${{\mathop{\rm B}\nolimits} = {\left( {{b_{ij}}} \right)_{p \times q}}}$,其克罗内克积为
${{\mathop{\rm A}\nolimits} \otimes {\mathop{\rm B}\nolimits} = \left( {\begin{array}{*{20}{c}}
{{a_{11}}{\mathop{\rm B}\nolimits} }& \cdots &{{a_{1n}}{\mathop{\rm B}\nolimits} }\\
\vdots & \ddots & \vdots \\
{{a_{m1}}{\mathop{\rm B}\nolimits} }& \cdots &{{a_{mn}}{\mathop{\rm B}\nolimits} }
\end{array}} \right)}$
如果${{\mathop{\rm x}\nolimits} = {\left( {{x_1}{,}{x_2}{,} \cdots{,}{x_n}} \right)^T}}$是向量,那么一元函数${f\left( x \right)}$的逐元向量函数定义为
${f\left( {\mathop{\rm x}\nolimits} \right) = {\left( {f\left( {{x_1}} \right){,}f\left( {{x_2}} \right){,} \cdots{,}f\left( {{x_n}} \right)} \right)^T}}$
如果${{\mathop{\rm X}\nolimits} = {\left( {{x_{ij}}} \right)_{m \times n}}}$是矩阵,那么一元函数${f\left( x \right)}$的逐元矩阵函数定义为
${f\left( {\mathop{\rm X}\nolimits} \right) = {\left( {f\left( {{x_{ij}}} \right)} \right)_{m \times n}}}$
2、导数公式
如果${{\mathop{\rm x}\nolimits} = {\left( {{x_1}{,}{x_2}{,} \cdots{,}{x_n}} \right)^T}}$,那么逐元向量函数的导数为
${f'\left( {\mathop{\rm x}\nolimits} \right) = {\left( {f'\left( {{x_1}} \right){,}f'\left( {{x_2}} \right){,} \cdots {,}f'\left( {{x_n}} \right)} \right)^T}}$
如果${{\mathop{\rm X}\nolimits} = {\left( {{x_{ij}}} \right)_{m \times n}}}$,那么逐元矩阵函数的导数为
${f'\left( {\mathop{\rm X}\nolimits} \right) = {\left( {f'\left( {{x_{ij}}} \right)} \right)_{m \times n}}}$
如果a、b、c和x是n维向量,A、B、C和X是n阶矩阵,那么
${\frac{{\partial \left( {{{\mathop{\rm a}\nolimits} ^T}{\mathop{\rm x}\nolimits} } \right)}}{{\partial {\mathop{\rm x}\nolimits} }} = \frac{{\partial \left( {{{\mathop{\rm x}\nolimits} ^T}{\mathop{\rm a}\nolimits} } \right)}}{{\partial {\mathop{\rm x}\nolimits} }} = {\mathop{\rm a}\nolimits} }$
${\frac{{\partial \left( {{{\mathop{\rm a}\nolimits} ^T}{\mathop{\rm X}\nolimits} {\mathop{\rm b}\nolimits} } \right)}}{{\partial {\mathop{\rm X}\nolimits} }} = {\mathop{\rm a}\nolimits} {{\mathop{\rm b}\nolimits} ^T}}$
${\frac{{\partial \left( {{{\mathop{\rm a}\nolimits} ^T}{\mathop{\rm X}\nolimits} {\mathop{\rm a}\nolimits} } \right)}}{{\partial {\mathop{\rm X}\nolimits} }} = \frac{{\partial \left( {{{\mathop{\rm a}\nolimits} ^T}{{\mathop{\rm X}\nolimits} ^T}{\mathop{\rm a}\nolimits} } \right)}}{{\partial {\mathop{\rm X}\nolimits} }} = {\mathop{\rm a}\nolimits} {{\mathop{\rm a}\nolimits} ^T}}$
${\frac{{\partial \left( {{{\mathop{\rm a}\nolimits} ^T}{{\mathop{\rm X}\nolimits} ^T}{\mathop{\rm X}\nolimits} {\mathop{\rm b}\nolimits} } \right)}}{{\partial {\mathop{\rm X}\nolimits} }} = {\mathop{\rm X}\nolimits} \left( {{\mathop{\rm a}\nolimits} {{\mathop{\rm b}\nolimits} ^T} + {{\mathop{\rm a}\nolimits} ^T}{\mathop{\rm b}\nolimits} } \right)}$
${\frac{{\partial \left( {{{\left( {{\mathop{\rm A}\nolimits} {\mathop{\rm x}\nolimits} + {\mathop{\rm a}\nolimits} } \right)}^T}{\mathop{\rm C}\nolimits} \left( {{\mathop{\rm B}\nolimits} {\mathop{\rm x}\nolimits} + {\mathop{\rm b}\nolimits} } \right)} \right)}}{{\partial {\mathop{\rm x}\nolimits} }} = {{\mathop{\rm A}\nolimits} ^T}{\mathop{\rm C}\nolimits} \left( {{\mathop{\rm B}\nolimits} {\mathop{\rm x}\nolimits} + {\mathop{\rm b}\nolimits} } \right) + {{\mathop{\rm B}\nolimits} ^T}{\mathop{\rm C}\nolimits} \left( {{\mathop{\rm A}\nolimits} {\mathop{\rm x}\nolimits} + {\mathop{\rm a}\nolimits} } \right)}$
${\frac{{\partial \left( {{{\mathop{\rm x}\nolimits} ^T}{\mathop{\rm A}\nolimits} {\mathop{\rm x}\nolimits} } \right)}}{{\partial {\mathop{\rm x}\nolimits} }} = \left( {{\mathop{\rm A}\nolimits} + {{\mathop{\rm A}\nolimits} ^T}} \right){\mathop{\rm x}\nolimits}}$
${\frac{{\partial \left( {{{\left( {{\mathop{\rm X}\nolimits} {\mathop{\rm b}\nolimits} + {\mathop{\rm c}\nolimits} } \right)}^T}{\mathop{\rm A}\nolimits} \left( {{\mathop{\rm X}\nolimits} {\mathop{\rm b}\nolimits} + {\mathop{\rm c}\nolimits} } \right)} \right)}}{{\partial {\mathop{\rm X}\nolimits} }} = \left( {{\mathop{\rm A}\nolimits} + {{\mathop{\rm A}\nolimits} ^T}} \right)\left( {{\mathop{\rm X}\nolimits} {\mathop{\rm b}\nolimits} + {\mathop{\rm c}\nolimits} } \right){{\mathop{\rm b}\nolimits} ^T}}$
${\frac{{\partial \left( {{{\mathop{\rm b}\nolimits} ^T}{{\mathop{\rm X}\nolimits} ^T}{\mathop{\rm A}\nolimits} {\mathop{\rm X}\nolimits} {\mathop{\rm c}\nolimits} } \right)}}{{\partial {\mathop{\rm X}\nolimits} }} = {{\mathop{\rm A}\nolimits} ^T}{\mathop{\rm X}\nolimits} {\mathop{\rm b}\nolimits} {{\mathop{\rm c}\nolimits} ^T} + {\mathop{\rm A}\nolimits} {\mathop{\rm X}\nolimits} {\mathop{\rm c}\nolimits} {{\mathop{\rm b}\nolimits} ^T}}$
3、激活函数
sigmoid函数:
${\sigma \left( x \right) = sigm\left( x \right) = \frac{1}{{1 + {e^{ - x}}}}}$
导数:
${\sigma '\left( x \right) = \left( {sigm\left( x \right)} \right)' = \sigma \left( x \right)\left( {1 - \sigma \left( x \right)} \right) = - \frac{{{e^{ - x}}}}{{{{\left( {1 + {e^{ - x}}} \right)}^2}}}}$
双曲正切函数tanh:
${tanh\left( x \right) = \frac{{{e^x} - {e^{ - x}}}}{{{e^x} + {e^{ - x}}}}}$
导数:
${\left( {tanh\left( x \right)} \right)' = 1 - {\left( {tanh\left( x \right)} \right)^2} = \frac{{{{\left( {{e^x} + {e^{ - x}}} \right)}^2} - {{\left( {{e^x} - {e^{ - x}}} \right)}^2}}}{{{{\left( {{e^x} + {e^{ - x}}} \right)}^2}}}}$
修正线性单元ReLU:
${ReLU\left( x \right) = max\left( {0{,}x} \right)}$
渗漏修正线性单元LReLU:
${LReLU\left( x \right) = \left\{ {\begin{array}{*{20}{c}}
{1{,}x \ge 0}\\
{ax{,}x < 0}
\end{array}} \right.}$
软最大输出函数softmax:
${softmax\left( {{x_1}{,}{x_2}{,} \cdots{,}{x_n}} \right) = \frac{1}{{\sum\limits_{i = 1}^n {exp\left( {{x_i}} \right)} }}{\left( {exp\left( {{x_i}} \right)} \right)_{n \times 1}}}$
4、梯度下降算法
梯度下降算法,是在无约束条件下计算连续可微函数极小值的基本方法。这种方法的核心思想是用
负梯度方向作为下降方向,在1874年由法国科学家Cauchy提出。
输入:${f\left( x \right)}$的表达式
输出:极小值点${{x^ * }}$
1. 选初始点${{x_0}}$,收敛误差${\varepsilon > 0}$,迭代次数为N,令k=0。
2. 若${\left| {\nabla f\left( {{x_k}} \right)} \right| \le \varepsilon }$,则${{x^ * } = {x_k}}$,停止迭代;否则计算${{\nabla f\left( {{x_k}} \right)}}$。
3. 选择和计算步长因子${{\alpha _k}}$。
4. 计算${{x_{k + 1}} = {x_k} - {\alpha _k}\nabla f\left( {{x_k}} \right)}$。
5. 令k=k+1,若${k \ge N}$,则${{x^ * } = {x_k}}$,停止迭代;否则转至步骤2。
随机梯度下降算法 (SGD)
采用严格的反向传播算法训练神经网络,需要同时考虑所有样本对梯度的贡献。如果样本的数量很大,那么梯度下降的每一次迭代都可能花费很长时间,从而可能导致整个过程收敛得非常缓慢。
随机梯度下降(Stochastic Gradient Descent,SGD)是一种对梯度下降优化方法的随机近似。其应用条件是目标函数能够表示成一组可微函数之和。
1)在线模式
在线模式是先把所有样本随机洗牌,再逐一计算每个样本对梯度的贡献去更新权值,即
${{w} = {w} - \eta \frac{{\partial {e_i}}}{{\partial {w}}}{,}l = 1{,}2{,} \cdots {,}L}$
其中,${{e_i}}$表示网络计算样本${{{x}^l}}$的实际输出与期望输出之间的误差。注意,这个按样本逐一更新权值的过程可能需要循环多次。
2) mini-batch 模式
在线模式的缺点是梯度下降的过程不太稳定、波动较大。一种折中的方法是采用“迷你块”mini-batch模式,实际上就是把所有样本随机洗牌后分为若干大小为m的块,再逐一计算每块对梯度的贡献去更新权值,即
${{w} = {w} - \eta \left[ {\frac{1}{m}\sum\limits_{l = \left( {i - 1} \right) \cdot m + 1}^{i \cdot m} {\frac{{\partial {e_l}}}{{\partial {w}}}} } \right]{,}i = 1{,}2{,} \cdots {,}\left\lfloor {L/m} \right\rfloor}$
为了改善随机梯度下降的训练效果,还常常使用权值衰减(weight decay)系数${\lambda}$,可得到
${{w} = \left( {1 - \lambda } \right){w} - \eta \left[ {\frac{1}{m}\sum\limits_{l = \left( {i - 1} \right) \cdot m + 1}^{i \cdot m} {\frac{{\partial {e_l}}}{{\partial {w}}}} } \right]{,}i = 1{,}2{,} \cdots {,}\left\lfloor {L/m} \right\rfloor}$
为了进一步提高稳定性,可以再引入一个动量项d及其加权系数${v}$,得到SGD的基本动量模式:
${{{d}_{l + 1}} = v{{d}_l} - \eta \left[ {\frac{1}{m}\sum\limits_{l = \left( {i - 1} \right) \cdot m + 1}^{i \cdot m} {\frac{{\partial {e_l}}}{{\partial {{w}_l}}}} } \right]{,}i = 1{,}2{,} \cdots {,}\left\lfloor {L/m} \right\rfloor {,}v > 0}$
${{{w}_{l + 1}} = \left( {1 - \lambda } \right){{w}_l}{ } + {{d}_{l + 1}} = \left( {1 - \lambda } \right){{w}_l} + v{{d}_l} - \eta \left[ {\frac{1}{m}\sum\limits_{l = \left( {i - 1} \right) \cdot m + 1}^{i \cdot m} {\frac{{\partial {e_l}}}{{\partial {{w}_l}}}} } \right]{,}i = 1{,}2{,} \cdots {,}\left\lfloor {L/m} \right\rfloor}$
注
随机梯度下降还有很多其他变种,重要包络Nesterov动量模式、Adagrad、Adadelta、RMSProp和Adam等。其中,Adam是目前最好的算法。
5、反向传播算法
深度神经网络的基本学习训练方法是反向传播算法,反向传播算法在本质上是一种具有递归结构的梯度下降算法,往往需要给定足够多的训练样本,才能获得满意的效果。
1)逐层反向传播算法
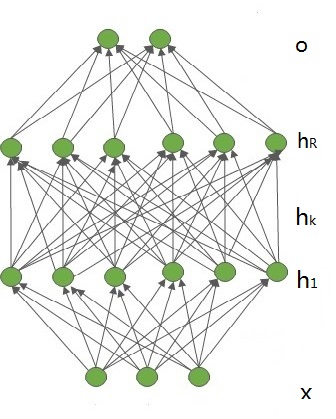
多层感知器由一个输入层、若干隐含层和一个输出层组成,如图所示。不妨设输入层的维数是m,输入向量表示为${x = {\left( {{x_1}{,}{x_2}{,} \cdots{,}{x_m}} \right)^T} \in {R^m}}$。第k个隐含层包含${{n_k}}$个神经元${\left( {k = 1{,}2{,} \cdots {,}R} \right)}$,相应的隐含层向量表示为${{{h}_k} = {\left( {{h_{k,1}}{,}{h_{k,2}}{,} \cdots{,}{h_{k,{n_k}}}} \right)^T} \in {R^{{n_k}}}}$。输出层包含c个神经元,输出向量表示为${{o} = {\left( {{o_1}{,}{o_2}{,} \cdots {,}{o_c}} \right)^T} \in {R^c}}$。输入层与第1个隐含层之间的权值矩阵用${{{W}^1} = {\left( {w_{ij}^1} \right)_{{n_1} \times m}}}$表示。第k-1个隐含层与第k个隐含层之间的权值矩阵用${{{W}^k} = {\left( {w_{ij}^k} \right)_{{n_k} \times {n_{k - 1}}}}\left( {1 < k \le R} \right)}$表示。第R个隐含层与输出层之间的权值矩阵用${{{W}^{R + 1}} = {\left( {w_{ij}^{R + 1}} \right)_{c \times {n_R}}}}$表示。那么,这个多层感知器的各层神经元激活输出可以计算如下:
${\left\{ {\begin{array}{*{20}{c}}{{{h}_1} = {\sigma _{{{h}_1}}}\left( {{{W}^1}{x + }{{b}^1}} \right)}\\
{{{h}_k} = {\sigma _{{{h}_k}}}\left( {{{W}^k}{{h}_{k - 1}}{ + }{{b}^k}} \right){,}2}\\
{{o} = {\sigma _{o}}\left( {{{W}^{R + 1}}{{h}_R}{ + }{{b}^{R + 1}}} \right)}
\end{array}} \right. \le k \le R}$
其中,${{{b}^1}}$、${{{b}^k}}$和${{{{b}^{R + 1}}}}$是各层的偏置;${{{\sigma _{{{h}_1}}}}}$、${{{\sigma _{{{h}_k}}}}}$和${{{\sigma _{o}}}}$是各层的逐元向量函数,一般都取为逐元sigmoid函数。
输入:训练集${\left\{ {\left( {{{x}^l},{{y}^l}} \right),{\rm{ 1}} \le l \le {\rm{L}}} \right\}}$,学习率${\eta }$,分层网络结构,迭代次数 epoch。
输出:所有权值和偏置${\left( {{{W}^k}{,}{{b}^k}} \right)\left( {1 \le k \le R + 1} \right)}$
1. 随机初始化${{{W}^k} \approx 0}$,${{{b}^k} \approx 0}$,${k = 1{,}2{,} \cdots {,}R + 1}$
2. 令${{h}_0^l = {x^l}}$
3. for ${i = 1{,}2{,} \cdots {,}epoch}$ do
4. for ${l = 1{,}2{,} \cdots {,}L}$ do
5. 计算${{u}_k^l = {{W}^k}{h}_{k - 1}^l + {{b}^k}}$,${{h}_k^l = \sigma \left( {{u}_k^l} \right)}$,${{1 \le k \le R + 1}}$
6. 计算${{\delta }_{R + 1}^l = \left( {{{o}^l} - {{y}^l}} \right) \circ \sigma '\left( {{u}_{R + 1}^l} \right)}$
7. 计算${{\delta }_k^l = \left[ {{{\left( {{{W}^{k + 1}}} \right)}^T}{\delta }_{k + 1}^l} \right] \circ \sigma '\left( {{u}_k^l} \right){,}1 \le k \le R}$
8. end for
9. 计算${\frac{{\partial E}}{{\partial {{W}^k}}} = \sum\limits_{l = 1}^L {{\delta }_k^l{{\left( {{h}_{k - 1}^l} \right)}^T}} }$,${\frac{{\partial E}}{{\partial {{b}^k}}} = \sum\limits_{l = 1}^L {{\delta }_k^l} }$,${1 \le k \le R + 1}$
10. 如果总梯度足够小,则停止
11. 否则,更新权值和偏置:${{{W}^k} \leftarrow {{W}^k} - \eta \frac{{\partial {L_N}}}{{\partial {{W}^k}}}}$,${{{b}^k} \leftarrow {{b}^k} - \eta \frac{{\partial {L_N}}}{{\partial {{b}^k}}}}$,${1 \le k \le R + 1}$
12. end for
2)误差函数
平方误差
为了对多层感知器中的权值和偏置进行学习,需要给定一组训练样本。假定共有L个训练样本${\left( {{{x}^l}{,}{{y}^k}} \right)\left( {1 \le l \le L} \right)}$,输入是${{{x}^l} = {\left( {{x}_1^l{,}{x}_2^l{,} \cdots {,}{x}_m^l} \right)^T}}$,期望输出是${{{y}^l} = {\left( {{y}_1^l{,}{y}_2^l{,} \cdots {,}{y}_c^l} \right)^T}}$,实际输出是${{{o}^l} = {\left( {o_1^l{,}o_2^l{,} \cdots {,}o_c^l} \right)^T}}$。把优化的目标函数选为平方误差:
${E = \frac{1}{2}\sum\limits_{l = 1}^L {{{\left\| {{{o}^l} - {{y}^l}} \right\|}^2}} = \frac{1}{2}\sum\limits_{l = 1}^L {\sum\limits_{j = 1}^c {{{\left\| {{o}_j^l - {y}_{^j}^l} \right\|}^2}} } }$
令${{h}_0^l = {{x}^l}}$,${{u}_k^l = {{W}^k}{h}_{k - 1}^l + {{b}^k}}$,${{h}_k^l = \sigma \left( {{u}_k^l} \right)\left( {1 \le k \le R + 1} \right)}$,${{{o}^l} = {h}_{R + 1}^l = \sigma \left( {{u}_{R + 1}^l} \right)}$。如果定义网络各层关于第${l}$个样本的反向传播误差信号的灵敏度为:
${\delta _k^l = \frac{{\partial E}}{{\partial {u}_k^l}}}$
那么这些反向传播误差信号可依次计算如下:
${\delta _{R + 1}^l = \frac{{\partial E}}{{\partial {u}_{R + 1}^l}} = \frac{{\partial E}}{{\partial {{o}^l}}} \cdot \frac{{\partial {{o}^l}}}{{\partial {u}_{R + 1}^l}} = \left( {{{o}^l} - {{y}^l}} \right) \circ \sigma '\left( {{u}_{R + 1}^l} \right) = \left( {{{o}^l} - {{y}^l}} \right) \circ {{o}^l} \circ \left( {1 - {{o}^l}} \right)}$
${\delta _k^l = \frac{{\partial E}}{{\partial {u}_k^l}} = \frac{{\partial E}}{{\partial {u}_{k + 1}^l}} \cdot \frac{{\partial {u}_{k + 1}^l}}{{\partial {u}_k^l}} = \left[ {{{\left( {{{W}^{k + 1}}} \right)}^T}\delta _{k + 1}^l} \right] \circ \sigma '\left( {{u}_k^l} \right){,1} \le {k} \le {R}}$
根据上式,可以总结为逐层反向传播算法。
交叉熵误差
${E = - \sum\limits_{l = 1}^L {\sum\limits_{j = 1}^c {\left( {{y}_{^j}^l \times log\left( {{o}_j^l} \right) + \left( {1 - {y}_{^j}^l} \right) \times log\left( {1 - {o}_j^l} \right)} \right)} } }$
这时,相应的逐层反向传播算法只需把${\delta _{R + 1}^l}$的计算公式修改为:
${\delta _{R + 1}^l = {{o}^l} - {{y}^l}}$
注
需要指出的是,多层感知器在训练完成之后,常常再被用软最大函数softmax转换为伪概率输出:
${{o} = softmax\left( {{{W}^{R + 1}}{{h}_R} + {{b}^{R + 1}}} \right)}$
若采用平方误差作为目标函数时, ${\delta _{R + 1}^l}$ 的计算公式改为:
${\delta _{R + 1}^l = \frac{{\partial E}}{{\partial {u}_{R + 1}^l}} = \frac{{\partial E}}{{\partial {{o}^l}}} \cdot \frac{{\partial {{o}^l}}}{{\partial {u}_{R + 1}^l}} = \left[ {diag\left( {{{o}^l}} \right) - {{o}^l}{{\left( {{{o}^l}} \right)}^T}} \right]\left( {{{o}^l} - {{y}^l}} \right)}$
若采用交叉熵误差作为目标函数时, ${\delta _{R + 1}^l}$ 的计算公式改为:
${\delta _{R + 1}^l = \left( {\begin{array}{*{20}{c}}
1&{\frac{{o_1^l}}{{o_2^l - 1}}}& \cdots &{\frac{{o_1^l}}{{o_c^l - 1}}}\\
{\frac{{o_2^l}}{{o_1^l - 1}}}&1& \cdots &{\frac{{o_2^l}}{{o_c^l - 1}}}\\
\vdots & \vdots & \vdots & \vdots \\
{\frac{{o_c^l}}{{o_1^l - 1}}}&{\frac{{o_c^l}}{{o_2^l - 1}}}& \cdots &1
\end{array}} \right)\left( {{{o}^l} - {{y}^l}} \right)}$
${= \left( {diag\left( {1./\left( {1 - {{o}^l}} \right)} \right) - {{\left( {{{o}^l}} \right)}^T}\left( {1./\left( {1 - {{o}^l}} \right)} \right)} \right)\left( {{{o}^l} - {{y}^l}} \right)}$
其中,“1”表示一个分量全是1的向量,“./”表示向量的对应分量相除。
如果每个样本的期望输出${{{{y}^l}}}$仅有一个分量,为${{y}_{jl}^l = 1}$,那么还可以选用退化交叉熵作为目标函数,即:
${E = - \sum\limits_{l = 1}^L {log\left( {o_{jl}^l} \right)} }$
同时,${\delta _{R + 1}^l}$ 的计算公式应修正为:
${\delta _{R + 1}^l = {{o}^l} - {{y}^l}}$
6、块归一化(batch normalization)
块归一化,又称为批量归一化。对神经网络的训练过程进行块归一化,不仅可以提高网络的训练速度,还可以提高网络的泛化能力。块归一化可以理解为把对输入数据的归一化扩展到其他层的输入数据进行归一化,以减小内部数据分布偏移的影响。经过块归一化后,一方面可以通过选择比较大的初始学习率极大提升训练速度,另一方面还可以不用太关心初始化方法和正则化技巧的选择,从而减少对网络训练过程的人工干预。
块归一化在理论上可以作用于任何变量,但在神经网络中一般直接作用隐含层单元的输入,不妨设x表示某个隐含层单元的输入。${B = \left\{ {\left. {{x_1}{,}{x_2}{,} \cdots {,}{x_m}} \right\}} \right.}$表示x的一个取值块。块归一化实际上是学习一个包含两个参数${\gamma}$和${\beta}$的变换${B{N_{\gamma {,}\beta }}}$,把${{x_i}}$变成${{y_i}}$,计算过程如下:
${\left\{ {\begin{array}{*{20}{c}}
{{\mu _B} \leftarrow \frac{1}{m}\sum\limits_{i = 1}^m {{x_i}} }\\
{{\sigma _B} \leftarrow \frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{x_i} - {\mu _B}} \right)}^2}} }\\
{{{\hat x}_i} \leftarrow \frac{{{x_i} - {\mu _B}}}{{\sqrt {\sigma _{_B}^2 + \varepsilon } }}}\\
{{y_i} \leftarrow \gamma {{\hat x}_i} + \beta \equiv B{N_{\gamma {,}\beta }}\left( {{{\hat x}_i}} \right)}
\end{array}} \right.}$
在学习训练完成之后,令均值${E\left[ x \right] = {E_B}\left[ {{\mu _B}} \right]}$、方差${V\left[ x \right] = \frac{m}{{m - 1}}{E_B}\left[ {\sigma _B^2} \right]}$,并把变换${y = B{N_{\gamma {,}\beta }}\left( {{{\hat x}_i}} \right)}$替换成下面的推理尺度变换:
${y = \frac{\gamma }{{\sqrt {V\left[ x \right] + \varepsilon } }} \cdot x + \left( {\beta - \frac{{\gamma E\left[ x \right]}}{{\sqrt {V\left[ x \right] + \varepsilon } }}} \right)}$
在应用时,块归一化通常被直接作用于某个或多个隐含层的所有输入。
7、权值偏置初始化
在训练神经网络之前,必须对其权值和偏置进行初始化。常用的初始化方法有三种:高斯初始化、Xavier初始化和MSRA初始化。它们一把都把偏置初始化为0,但对权值进行随机初始化。
1)高斯初始化
权值:根据高斯分布初始化,均值选为0, 方差人工选择。
2)Xavier初始化
如果神经元有n个输入,则${{{w}_{ij}} \sim U\left[ { - \frac{1}{{\sqrt N }}{,}\frac{1}{{\sqrt N }}} \right]}$,b=0。
3)MSRA初始化
如果神经元有n个输入,则 ${{{w}_{ij}} \sim N\left[ {0{,}\frac{2}{n}} \right]}$,b=0。
8、权值丢失(dropout)
在训练神经网络时,如果训练样本较少,一般就需要考虑采用某些正则化技巧来防止过拟合。权值丢失是一种简单有效的正则化技巧,其基本思想是通过阻止特征检测器的共同作用来提高神经网络的泛化能力。主要包括丢失输出和丢失连接。
1)丢失输出
丢失输出是指在神经网络的训练过程中随机让网络的某些节点(包括输入和隐含节点)不工作。
2)丢失连接
丢失连接是指在神经网络的训练过程中随机让网络的某些连接不工作。
参考文献
[1] 李玉鑑等. 深度学习:卷积神经网络从入门到精通, 北京:机械工业出版社,2018.





 浙公网安备 33010602011771号
浙公网安备 33010602011771号