机器学习知识点目录

监督学习

回归

线性回归

线性回归表达式

\[\hat{y} = w x + b \]

其中，\(\hat{y}\)表示预测值，\(\theta_0\)表示截距，\(\theta_1\)到\(\theta_n\)表示回归系数，\(x_1\)到\(x_n\)表示特征。

代价函数

\[J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (\hat{y}^{(i)} - y^{(i)})^2 \]

其中，\(m\)表示样本数量，\(\hat{y}^{(i)}\)表示第\(i\)个样本的预测值，\(y^{(i)}\)表示第\(i\)个样本的真实值。

梯度下降

梯度下降的思想是：

通过计算当前参数的梯度，沿着梯度的反方向，不断更新参数，直到达到最优解。

\[w := w - \alpha \frac{\partial J(\theta)}{\partial w}\\ b := b - \alpha \frac{\partial J(\theta)}{\partial b} \]

其中，\(\alpha\)表示学习率，即参数更新的步长。

多参数线性回归

多参数线性回归表达式

\[\hat{y} = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_n x_n \]

其中，\(\theta_0\)表示截距，\(\theta_1\)到\(\theta_n\)表示回归系数，\(x_1\)到\(x_n\)表示特征。

梯度

\[\frac{\partial J(\theta)}{\partial \theta_j} = \frac{1}{m} \sum_{i=1}^{m} (\hat{y}^{(i)} - y^{(i)}) x_j^{(i)} \]

其中，\(m\)表示样本数量，\(\hat{y}^{(i)}\)表示第\(i\)个样本的预测值，\(y^{(i)}\)表示第\(i\)个样本的真实值，\(x_j^{(i)}\)表示第\(i\)个样本的第\(j\)个特征。

梯度下降表示为：

\[\theta_j := \theta_j - \alpha \frac{\partial J(\theta)}{\partial \theta_j} \]

多项式回归

多项式回归表达式

\[\hat{y} = \theta_0 + \theta_1 x + \theta_2 x^2 + \cdots + \theta_n x^n \]

特征缩放

当特征的取值范围差异较大时，可以对特征进行缩放，使得特征的取值范围在\([-1, 1]\)或\([0, 1]\)之间。

  1. 特征值除以最大值
  2. 均值归一化：

    \[x' = \frac{x - \mu}{\sigma} \]

  3. z-score归一化：

    \[x' = \frac{x - \mu}{\sigma},\sigma=\sqrt{\frac{1}{m} \sum_{i=1}^{m} (x^{(i)} - \mu)^2} \]

分类

二元分类的表达式

\[h_{\theta}(x) = g(\theta^T x) = \frac{1}{1 + e^{-\theta^T x}} \]

其中，\(g(z)\)表示Sigmoid函数，其表达式为：

\[g(z) = \frac{1}{1 + e^{-z}} \]

决策边界

决策边界是指分类器在两个类别之间的分界线。

表达式为：

\[\theta^T x = 0 \]

代价函数

\[J(\theta) = -\frac{1}{m} \sum_{i=1}^{m} [y^{(i)} \log h_{\theta}(x^{(i)}) + (1 - y^{(i)}) \log (1 - h_{\theta}(x^{(i)}))] \]

梯度下降

\[\theta_j := \theta_j - \alpha \frac{\partial J(\theta)}{\partial \theta_j} \]

其中，\(\alpha\)表示学习率，即参数更新的步长。

\[\frac{\partial J(\theta)}{\partial \theta_j} = \frac{1}{m} \sum_{i=1}^{m} (h_{\theta}(x^{(i)}) - y^{(i)}) x_j^{(i)} \]

正则化

过拟合

解决过拟合的方法有：

  • 增加训练集的数量
  • 减少特征的数量
  • 正则化

L2正则化

正则化的思想是：在代价函数中增加一个正则化项，使得参数的值尽可能小。

\[J(\theta) = -\frac{1}{m} \sum_{i=1}^{m} [y^{(i)} \log h_{\theta}(x^{(i)}) + (1 - y^{(i)}) \log (1 - h_{\theta}(x^{(i)}))] + \frac{\lambda}{2m} \sum_{j=1}^{n} \theta_j^2 \]

其中，\(\lambda\)表示正则化参数，\(n\)表示特征的数量。

梯度下降

\[\frac{\partial J(\theta)}{\partial \theta_j} = \frac{1}{m} \sum_{i=1}^{m} (h_{\theta}(x^{(i)}) - y^{(i)}) x_j^{(i)} + \frac{\lambda}{m} \theta_j \]

神经网络

神经元模型

  • 输入部分：多个输入/树突
  • 处理部分：神经核
  • 输出部分：单个输出/轴突

神经网络层

  • 输入层：接收输入信号
  • 隐藏层：处理输入信号，从输入特征中提取特征
  • 激活函数：激活函数将原始输入转换为激活值，用于传递给下一层
  • 输出层：输出最终结果

激活函数

激活函数的作用是引入非线性因素，使得神经网络可以解决非线性问题。如果没有激活函数，即使有再多的隐藏层，也只相当于一个隐藏层，因为多个线性层的叠加仍然是线性的。

常用的激活函数有：

  1. Sigmoid函数

    \[g(z) = \frac{1}{1 + e^{-z}} \]

    • 优点：输出值在0到1之间，单调连续，输出范围有限，容易求导
    • 缺点：容易出现梯度消失，输出不是以0为中心

  2. ReLU函数

    \[g(z) = \max(0, z) \]

    • 优点：收敛速度快
    • 缺点：容易出现梯度消失，输出不是以0为中心

  3. softmax函数

    \[g(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{n} e^{z_j}} \]

    • softmax是sigmoid函数的推广，用于多分类问题

多层神经网络

多层神经网络的结构为：

img

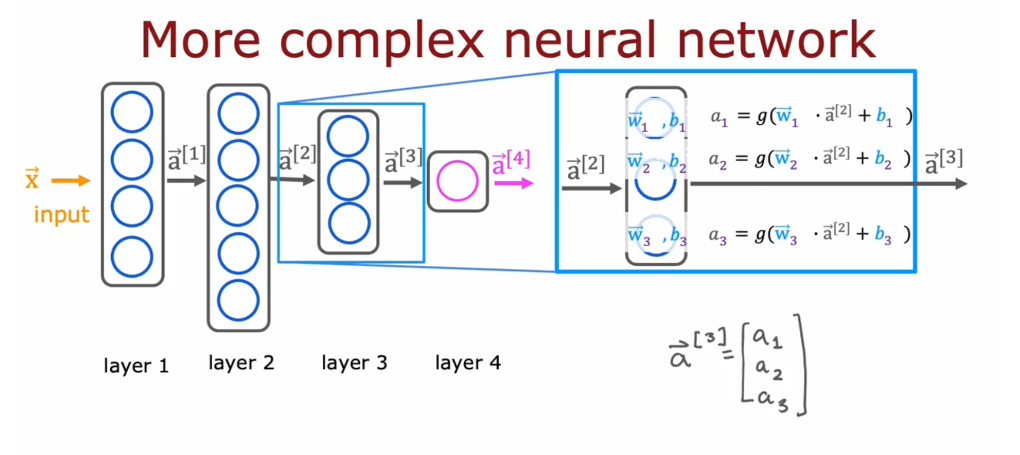
公式表达为：

\[a^{[i]}_j = g^{[i]}(z^{[i]}_j) = g^{[i]}(\sum_{k=1}^{n^{[i-1]}} w^{[i]}_{jk} a^{[i-1]}_k + b^{[i]}_j) \]

前向传播

前向传播的过程是：

  1. 将输入信号传递给第一层神经元
  2. 第一层神经元将信号传递给第二层神经元
  3. 第二层神经元将信号传递给第三层神经元
  4. 以此类推，直到输出层

TensorFlow实现

#构建模型
model = keras.Sequential([
    keras.layers.Dense(64, activation='relu'),
    keras.layers.Dense(64, activation='relu'),
    keras.layers.Dense(10, activation='softmax')
])

#编译模型
model.compile(optimizer=tf.train.AdamOptimizer(),
              loss='sparse_categorical_crossentropy')

#训练模型
model.fit(train_images, train_labels, epochs=5)

#评估准确率
test_loss, test_acc = model.evaluate(test_images, test_labels)

#进行预测
predictions = model.predict(test_images)

模型评估

交叉验证

交叉验证的思想是：将训练集分成训练集、验证集和测试集，训练集用于训练模型，验证集用于调整模型的参数，测试集用于评估模型的性能。

  • 训练误差：训练集上的误差，用于评估模型的拟合能力
  • 验证误差：验证集上的误差，用于评估模型的泛化能力
  • 测试误差：测试集上的误差，用于评估模型的泛化能力

偏差和方差

  • 偏差：模型预测值与真实值之间的差距
  • 方差：模型预测值与模型预测值的平均值之间的差距

通过增加模型的复杂度，可以降低偏差，但是会增加方差；通过减少模型的复杂度，可以降低方差，但是会增加偏差。

精确率和召回率

  • 精确率：预测为正的样本中，真正为正的样本的比例

    \[\text{精确率} = \frac{TP}{TP + FP} \]

  • 召回率：真正为正的样本中，预测为正的样本的比例

    \[\text{召回率} = \frac{TP}{TP + FN} \]

    F1值是精确率和召回率的调和平均值，它的取值范围为\([0, 1]\)，F1值越大，模型的性能越好。

    \[\text{F1值} = \frac{2}{\frac{1}{\text{精确率}} + \frac{1}{\text{召回率}}} = \frac{2PR}{P + R} \]

决策树

决策树定义

决策树是一种基本的分类与回归方法，是一种树形结构，其中每个非叶子节点表示一个特征属性上的测试，

每个分支代表这个特征属性在某个值域上的输出，每个叶子节点存放一个类别。

img

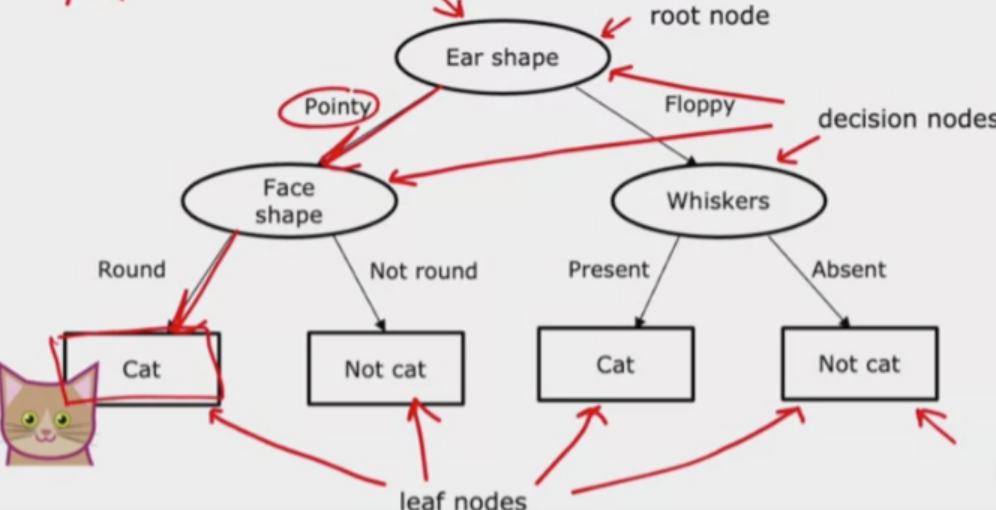
决策树的构建

分割特征的选择

信息熵

信息熵是度量样本集合纯度最常用的一种指标。

\[H(X) = -\sum_{i=1}^{n} p_i \log p_i \]

其中，\(p_i\)表示第\(i\)个类别的概率。

信息增益

信息增益表示得知特征\(X\)的信息而使得类\(Y\)的信息的不确定性减少的程度。

\[\text{信息增益} = H(Y) - H(Y|X) \]

其中，\(H(Y)\)表示类别\(Y\)的信息熵，\(H(Y|X)\)表示特征\(X\)给定的条件下类别\(Y\)的条件熵。

停止条件

  • 当前节点中的样本全部属于同一类别
  • 当树的深度达到预先设定的最大深度
  • 分割带来的杂质下降不大于预先设定的阈值
  • 当前节点中的样本个数小于预先设定的阈值

递归构建

  1. 选择最优特征
  2. 根据最优特征划分数据集
  3. 递归构建决策树

复杂特征值的处理

独热编码

独热编码的思想是：将离散特征的每个取值都看作是一个新的特征，如果该样本的该特征取值为该特征的取值，则该特征的值为1，否则为0。

连续特征值的处理

  1. 将连续特征值离散化
  2. 选择最优划分点

回归树

回归树同决策树类似，只是回归树的叶子节点存放的是一个数值，而不是一个类别。回归树完成了对数据的回归拟合

在回归树中，分裂特征的选择：选择一个特征和一个分割点，使得分割后的两个子集的均方差最小.

树集

多决策树

多决策树的思想是：通过多个决策树的投票，来决定最终的分类结果。

随机森林

在构建树集成时，有放回抽样可以用于从原始数据集中生成多个不同的训练子集，以便为每个子集训练一个独立的决策树，确保树集成中的决策树具有足够的多样性，提高模型的健壮性。

从训练集中使用有放回抽样的方式抽取m个特征，作为决策树的分割特征。m一般取\(\sqrt{n}\)，其中\(n\)表示特征的数量。

XGBoost实现

#构建模型
model = XGBClassifier()

#训练模型
model.fit(train_images, train_labels)

#进行预测
predictions = model.predict(test_images)

无监督学习

聚类

聚类的定义

聚类是一种无监督学习，它将相似的对象归到同一个簇中。聚类的目标是使得簇内的对象尽量相似而簇间的差异尽量大。

K-means算法

K-means是一种典型的聚类算法，它的基本思想是：以空间中K个点为中心进行聚类，对最靠近他们的对象归类。通过迭代的方法，逐次更新各聚类中心的值，直到得到最好的聚类结果。

K-means算法流程

  1. 随机K个点作为聚类中心
  2. 计算每个点到聚类中心的距离，将每个点归到距离最近的聚类中心
  3. 重新计算每个聚类中心的值
  4. 重复2、3步骤，直到聚类中心的值不再变化

K-means算法的优化

成本函数

\[J(c^{(1)},...,c^{(m)},\mu_1,...,\mu_k)=\frac{1}{m}\sum_{i=1}^{m}||x^{(i)}-\mu_{c^{(i)}}||^2 \]

其中，\(c^{(i)}\)表示样本\(x^{(i)}\)所属的簇，\(\mu_{c^{(i)}}\)表示样本\(x^{(i)}\)所属的簇的中心点。

聚类中心

初始化聚类中心

通过随机选择K个点作为聚类中心，然后进行迭代，直到收敛。

多次随机初始化，选择代价函数最小的聚类中心。

中心数量的选择

  • 通过肘部法则选择最优的聚类中心数量。

肘部法则：随着聚类中心数量的增加，代价函数的值会逐渐减小，当聚类中心数量达到某个值时，代价函数的值会突然变化，这个值就是最优的聚类中心数量。

  • 根据业务需求选择聚类中心数量。

异常检测

异常检测的定义

异常检测是一种无监督学习，它的目标是识别出与大多数其他对象显著不同的数据对象。

异常检测的算法流程

高斯分布

高斯分布又称正态分布，它的概率密度函数为：

\[p(x;\mu,\sigma^2) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \]

其中，\(\mu\)表示均值，\(\sigma^2\)表示方差。

算法流程

  1. 选择特征\(x_i\)，计算均值\(\mu_i\)和方差\(\sigma_i^2\)

    确保特征符合高斯分布，如果不符合，可以对特征进行转换，使其符合高斯分布

  2. 计算概率\(p(x)\)
  3. 如果\(p(x) < \epsilon\)，则判断为异常

在具有多个特征的情况下，可以将多个特征的概率相乘，得到最终的概率。

\[p(x) = \prod_{j=1}^{n} p(x_j;\mu_j,\sigma_j^2) \]

推荐系统

推荐系统的定义

推荐系统是一种信息过滤系统，它的目标是预测用户对物品的评分或者喜好，从而为用户生成推荐列表。

协同过滤算法

损失函数

对于用户\(j\)对项目\(i\)的评分\(y^{(i,j)}\)，预测值为\((\theta^{(j)})^T x^{(i)}\)，损失函数为：

\[J(x^{(1)},...,x^{(n_u)},\theta^{(1)},...,\theta^{(n_m)}) = \frac{1}{2} \sum_{(i,j):r(i,j)=1} ((\theta^{(j)})^T x^{(i)} - y^{(i,j)})^2 + \frac{\lambda}{2} \sum_{i=1}^{n_m} \sum_{k=1}^{n} (\theta_k^{(i)})^2 + \frac{\lambda}{2} \sum_{i=1}^{n_u} \sum_{k=1}^{n} (x_k^{(i)})^2 \]

其中，\(n_u\)表示用户的数量，\(n_m\)表示项目的数量，\(n\)表示特征的数量，\(r(i,j)\)表示用户\(j\)是否对项目\(i\)评分。

对于二元标签分类，用户\(j\)对项目\(i\)的评分\(y^{(i,j)}\)，预测值为\(\sigma((\theta^{(j)})^T x^{(i)})\)，损失函数为：

\[J(x^{(1)},...,x^{(n_u)},\theta^{(1)},...,\theta^{(n_m)}) = -\frac{1}{m} \sum_{(i,j):r(i,j)=1} [y^{(i,j)} \log \sigma((\theta^{(j)})^T x^{(i)}) + (1 - y^{(i,j)}) \log (1 - \sigma((\theta^{(j)})^T x^{(i)}))] + \frac{\lambda}{2} \sum_{i=1}^{n_m} \sum_{k=1}^{n} (\theta_k^{(i)})^2 + \frac{\lambda}{2} \sum_{i=1}^{n_u} \sum_{k=1}^{n} (x_k^{(i)})^2 \]

梯度下降

\[x_k^{(i)} := x_k^{(i)} - \alpha \frac{\partial J}{\partial x_k^{(i)}}\\ \theta_k^{(j)} := \theta_k^{(j)} - \alpha \frac{\partial J}{\partial \theta_k^{(j)}} \]

均值化归一

为了合理预测未评分用户的评分，需要对用户的评分进行均值化归一。

\[y^{(i,j)} = y^{(i,j)} - \mu_i \]

其中，\(\mu_i\)表示用户\(i\)的评分均值。

相似度计算

相似度计算采用欧式距离，查找与用户\(j\)相似的用户，计算公式为：

\[d(x,y) = \sqrt{\sum_{i=1}^{n} (x_i - y_i)^2} \]

基于内容的推荐系统

基于内容的推荐系统的思想是：根据项目内容，计算用户的特征，然后根据用户的特征，为用户生成推荐列表。

系统流程

  1. 从项目中提取特征
  2. 计算用户的特征
  3. 特征向量化
  4. 计算用户与项目的相似度

特征提取

采用深度学习的方法，将项目的内容作为输入，将项目的特征作为输出。

项目特征向量和用户特征向量的维度相同。

img

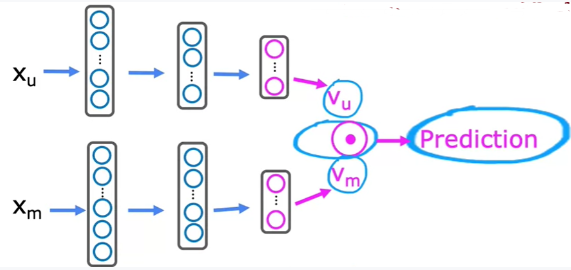
大型数据集处理

  1. 检索
    1. 生成一系列的候选集
    2. 从候选集中生成推荐列表
  2. 排序
    1. 利用深度学习对推荐列表进行评分
    2. 对评分进行排序，得到最终的推荐列表

强化学习

强化学习的定义

强化学习是一种无监督学习，它的目标是采取行动，感知环境，从而获得最大的奖励。

回报和策略

回报

强化学习的回报是指智能体在环境中采取行动后获得的奖励。

\[R=R_1+\gamma R_2+\gamma^2 R_3+...=\sum_{t=1}^{\infty}\gamma^{t-1}R_t \]

其中，\(R_t\)表示第\(t\)步的奖励，\(\gamma\)表示折扣因子，\(\gamma \in [0,1]\)。

策略

策略是指智能体在环境中采取行动的方式，它是状态到动作的映射。

\[a_t=\pi(s_t) \]

马尔可夫决策过程

马尔可夫决策过程是一种强化学习的模型，它的特点是：当前状态的奖励与之前的状态无关。

\[P(s_{t+1}|s_t)=P(s_{t+1}|s_1,...,s_t) \]

值函数

状态动作值函数

状态动作值函数是指在状态\(s\)下采取行动\(a\)的价值。

\[Q^{\pi}(s,a)=E_{\pi}[R_t|s_t=s,a_t=a] \]

其中，\(E_{\pi}\)表示在策略\(\pi\)下的期望。

贝尔曼方程

贝尔曼方程是状态动作值函数的递归表达式，它表示当前状态动作值函数等于下一个状态动作值函数加上当前的奖励，即：

\[ Q^{\pi}(s,a)=R_{t+1}+\gamma E[Q^{\pi}(s_{t+1},a_{t+1})] \]

深度强化学习

深度强化学习的思想是：利用深度学习来估计状态动作值函数。

算法流程

  1. 构建神经网络
    img
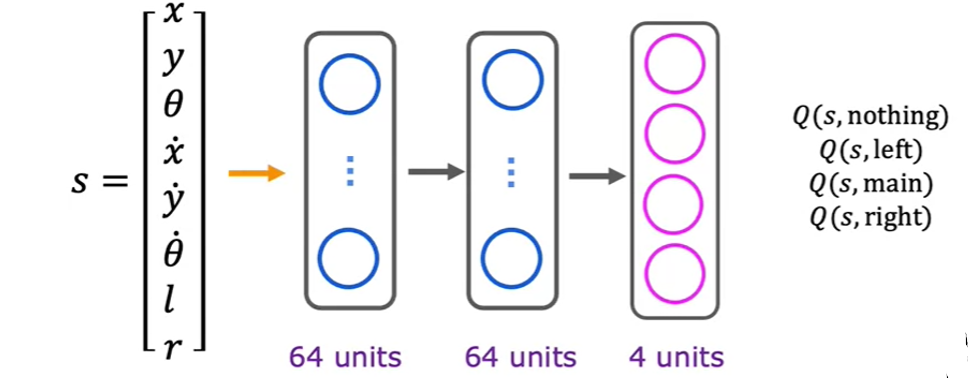
  2. 采用\(\epsilon\)-贪心策略选择动作

    \(\epsilon\)-贪心策略：以\(\epsilon\)的概率随机选择动作，以\(1-\epsilon\)的概率选择当前状态下的最优动作

  3. 采用经验回放的方式训练神经网络

    经验回放：将智能体的经验存储在经验池中，然后从经验池中随机抽取一批经验，用于训练神经网络

posted @ 2023-10-22 11:42  asdio  阅读(54)  评论(0)    收藏  举报