NP问题的算法设计技术

概述

用计算机来求解人类所面临的各种问题，问题本身的内在复杂性决定了求解这个问题的算法的计算复杂性

Turing论题

一个问题是可计算的当且仅当它在图灵机上经过有限步骤最后得到正确的结果

Turing论题把人类面临的所有问题划分成两类：

• 可计算问题
• 不可计算问题

Turing论题中“有限步骤”是一个相当宽松的条件，即使需要计算几个世纪的问题，在理论上也都是可计算的。因此Turing论题界定出的可计算问题几乎包括了人类遇到的所有问题

不可计算问题

• 停机问题
  给定一个计算机程序和一个特定的输入，判断该程序是否可以停机
  如果停机问题是可计算的，那么编译系统就能够在运行程序之前检查出程序中是否有死循环，事实上，当一个程序处于死循环时，系统无法确切地知道它只是一个很慢的程序，还是一个进入死循环的程序
• 判断一个程序中是否包含计算机病毒
  不存在一个病毒检测程序，能够检测出所有未来的新病毒

可计算问题

理论上可计算的问题不一定是实际可计算的。

• cook论题
  一个问题是实际可计算的当且仅当它在一个多项式时间内可计算
• 易解问题
  在多项式时间内可计算，在可以接受的时间内实现的问题
• 难解问题
  在多项式时间内可计算，但是在不可接受的时间内实现的问题

NP问题

求解一个问题往往比较困难，但是验证一个问题的解是否正确却相对容易

从是否可以被验证的角度，将难解问题分为两类：

• NP问题
• 非NP问题

判定问题

判定问题是要求回答“yes”或“no”的问题。

在实际应用中，很多问题以求解或计算的形式出现，但是，大多数问题可以很容易转化为相应的判定问题

确定性算法和P问题

确定性算法是指整个执行的过程中，每一步都有一个确定的选择，对于同一输入实例，算法的执行过程是唯一的

P问题是指对于规模为n的输入实例，确定性算法的执行时间不超过多项式函数的问题

P:Polynomial 多项式

所有易解问题都属于 P 类问题

非确定性算法和NP问题

非确定性算法是指整个执行的过程中，采用猜测验证方式的算法

• 猜测阶段：猜测一个可能的解
• 验证阶段：
  • 验证是否合理
  • 验证是否正确

非确定性算法不是一个实际可行的算法

NP类问题是指对于规模为n的输入实例，非确定性算法的验证时间不超过多项式函数的问题

对于 NP 类判定问题，关键是该问题存在一个确定性算法，并且能够以多项式时间检查和验证在猜测阶段所产生的答案

NP:nondeterministic polynomial 非确定性多项式

• NP类问题是难解问题的一个子集
  并不是任何一个在常规计算机上需要指数时间的问题（即难解问题）都是 NP 类问题
• P 类问题属于 NP 类问题
  P 类问题存在多项式时间的确定性算法进行判定或求解，显然也可以构造多项式时间的非确定性算法进行判定

NP完全问题

问题变换

问题变换是指将一个问题转化为另一个问题的过程

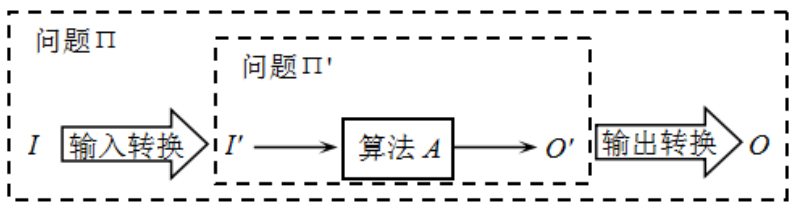
若在\(O(τ(n))\)的时间内完成上述输入和输出转换，则称问题 \(Π\) 以 \(τ(n)\) 时间变换到问题 \(Π'\)，记为 \(Π∝_{τ(n)}Π'\)，其中，\(n\) 为问题规模；

若在多项式时间内完成上述输入和输出转换，则称问题 \(Π\) 以多项式时间变换到问题 \(Π'\)，记为\(Π∝_{p}Π'\)。

问题变换的主要目的不是给出解决一个问题的算法，
而是给出比较两个问题计算复杂性的一种方式

NP完全问题

令 \(Π\) 是一个判定问题，如果问题 \(Π\) 属于 NP 类问题，并且对 NP 类问题中的每一个问题 \(Π'\)，都有 \(Π' ∝_pΠ\)，则称判定问题 \(Π\) 是一个NP完全问题，也称 NPC 问题

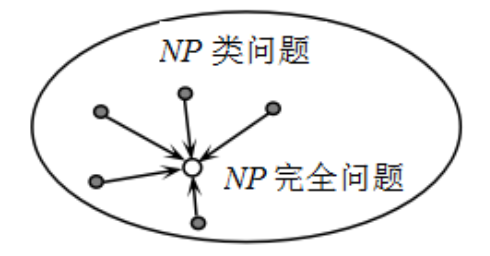
NP 完全问题有一个重要性质：如果一个 NP 完全问题能够在多项式时间内得到求解，那么 NP 类问题中的每一个问题都可以在多项式时间内得到求解

NP类问题的计算机解决

• 先进的算法设计技术
• 充分利用限制条件
• 近似算法
• 概率算法
• 并行算法
• 智能算法

近似算法

近似算法的基本思想是用近似最优解代替最优解，以换取算法设计上的简化和时间复杂性的降低。换言之，近似算法找到的可能不是一个最优解，但一定会为待求解的问题提供一个解

近似算法的衡量

假设近似算法求解最优化问题，且每个可行解对应的目标函数值均为正数。若一个最优化问题的最优值为c*，求解该问题的近似算法求得的近似最优值为 c，则将该近似算法的近似比 定义为：

\[η=\max(\frac{c}{c*},\frac{c*}{c}) \]

或用相对误差λ 表示近似算法的近似程度，定义为

\[λ=|\frac{c-c*}{c*}| \]

概率算法

概率算法允许算法在执行过程中随机选择下一步该如何进行，同时允许结果以较小的概率出现错误，并以此为代价，获得算法运行时间的大幅度减少

概率算法的基本特征：

• 概率算法对于相同的输入实例，概率算法的执行时间可能不同；
• 概率算法的结果不能保证一定是正确的，但可以限定其出错概率；
• 概率算法在不同的运行中，对于相同的输入实例可能会得到不同的结果。

概率算法通常分析平均情况下的期望时间复杂度，即在相同输入实例上重复执行概率算法的平均时间

舍伍德型概率算法

很多算法对于不同的输入实例，运行时间差别很大。此时，可采用舍伍德型概率算法来消除算法的时间复杂度与输入实例间的依赖关系

舍伍德型概率算法的有两种应用方式：

• 在确定性算法的某些步骤引入随机因素，将确定性算法改造成舍伍德型概率算法；
• 借助于随机预处理技术，不改变原有的确定性算法，仅对输入实例进行随机处理（称为洗牌），然后再执行确定性算法

拉斯维加斯型概率算法

拉斯维加斯型概率算法对同一个输入实例反复多次运行算法，直至运行成功，获得问题的解。如果运行失败，在相同的输入实例上再次运行算法

拉斯维加斯型概率算法的基本特征：

• 拉斯维加斯型概率算法的随机性选择有可能导致算法找不到问题的解，即算法运行一次，或者得到一个正确的解，或者无解。
• 只要出现失败的概率不占多数，当算法运行失败时，在相同的输入实例上再次运行概率算法，就又有成功的可能

拉斯维加斯型概率算法找到正确解的概率随着运行次数的增加而提高

蒙特卡罗型概率算法

对于许多问题来说，近似解毫无意义，如判定问题、整数因子划分问题

蒙特卡罗型概率算法的基本特征：

• 蒙特卡罗型概率算法用于求问题的准确解。
• 蒙特卡罗型概率算法偶尔会出错，但无论任何输入实例，总能以很高的概率找到一个正确解。
• 蒙特卡罗型概率算法总是给出解，但是，这个解偶尔可能是不正确的，一般情况下，也无法有效地判定得到的解是否正确。
• 蒙特卡罗型概率算法求得正确解的概率依赖于算法的运行次数，算法运行的次数越多，得到正确解的概率就越高。

例题：主元素问题

问题

设\(A[n]\)是含有 \(n\) 个元素的数组，\(x\) 是数组\(A[n]\)的一个元素，如果数组有一半以上的元素与 \(x\) 相同，则称元素 \(x\) 是数组\(A[n]\)的主元素。例如，在数组\(A[7]={3, 2, 3, 2, 3, 3, 5}\)中，元素 3 就是主元素

分析

• 随机地选择数组的一个元素\(A[i]\) 进行统计
  • 该元素出现的次数大于 \(n/2\)，则该元素就是数组的主元素，算法返回 1
  • 随机选择的元素 \(A[i]\) 不是主元素，算法返回 0
    • 数组 \(A[n]\) 没有主元素
    • 数组 \(A[n]\) 有主元素但不是元素 \(A[i]\)
• 再次运行蒙特卡罗型概率算法，直至算法返回 1，或者达到给定的错误概率

实现

int MajorityMC(int A[ ], int n)
{
    int i, j, count = 0;
    i = Random(0, n-1);                      //随机选择一个数组元素
    for (j = 0; j < n; j++)
        if (A[j] == A[i]) count++;
    if (count > n/2) return A[i];                //A[i]是主元素
    else return 0;
   }

群智能算法

群智能（算法模拟群体动物的社会行为机制，通过定义个体行为和群体行为，使群体具有种群多样化与行为指向性，利用群体优势，为复杂问题提供解决方案

遗传算法

模拟自然选择和遗传机制等生物进化过程的计算模型，从任意初始种群出发，通过选择、交叉和变异等遗传操作，使种群进化到搜索空间中越来越好的区域，直至达到最优解

遗传算法是一种随机的优化与搜索方法，具有并行性、通用性、全局优化性、健壮性、可操作性与简单性等特点，成为信息科学、计算机科学、运筹学和应用数学等诸多学科共同关注的热点研究领域

遗传算法的框架

算法：遗传算法的一般框架
输入：问题模型，pr、pc和pm
输出：最优解
       1. 设置种群个数 N，随机初始化种群 P(0)，t = 0；
       2. 重复下述操作，直到满足终止条件
           2.1 对种群 P(t) 的每个个体执行下述操作：
                 2.1.1 计算个体的适应值；
                 2.1.2 根据个体适应值及选择策略确定个体的选择概率 pi；
                 2.1.3 在[0, 1]区间确定一个随机数 r；
                 2.1.4 根据 r、pi 和 pr 执行选择操作，将个体加到种群 P(t+1)；
           2.2 对 P(t+1) 以概率pc执行交叉操作，并将结果加到种群 P(t+1)；
           2.3 对 P(t+1) 以概率pm执行变异操作，并将结果加到种群 P(t+1)；
           2.4 t = t + 1；
      3. 返回种群中适应值最大的个体；

遗传问题需要解决以下冠军问题

• 编码方式
  遗传算法需要采用某种编码方式将解空间映射到编码空间，每个编码对应问题的一个可能解，称为染色体或个体。编码空间可以是位串、实数等
• 初始种群
  种群是在编码空间根据适应值或某种竞争机制选择若干个个体组成的群体，通常采用随机方法产生初始种群，种群中个体的数量称为种群规模。如果种群规模太小，遗传算法容易陷入局部最优解，如果种群规模太大，遗传算法的计算量会很大，因此，种群规模会影响遗传算法的结果和效率。经验表明，种群规模一般取 20~100
• 适应度函数
  适应度用来评价种群中每个个体在优化过程中可能达到最优解的程度，度量个体适应度的函数称为适应度函数
  适应度函数非常重要。通常情况下，适应度函数与目标函数密切相关，有时直接将目标函数作为适应度函数
• 遗传操作
  • 选择：从当前个体中按照一定的概率选出优良的个体，实现方法通常有轮盘赌法选择、竞争选择、排序选择、稳态选择等
  • 交叉：将两个个体相互混合，产生由双方基因组成的新个体，实现方法有单点交叉、多点交叉、均匀交叉等
  • 变异：将个体编码的一些位进行随机变化，实现方法有定概率变异、变概率变异、预测变异等。
• 控制参数
  遗传算法必须精心选择以下参数：种群规模、染色体长度、杂交概率、变异概率、终止条件等，这些参数的选择对遗传算法的最终结果和效率影响很大。
  由于遗传算法无法用传统的方法来判定算法是否收敛以终止算法，常用的方法是预先设定一个最大的进化代数，或算法在连续多少代以后解的适应值没有明显改进

蚁群算法

蚂蚁个体之间通过信息素进行信息传递，从而相互协作，表现出复杂有序的行为

蚁群算法作为群智能算法的典型方法，通过模拟生物寻优能力来解决实际问题，具有较强的鲁棒性、通用性、快速性、全局性、并行搜索等优点，受到学术界的广泛关注

蚁群算法根据信息正反馈原理，在路径寻优的过程中主要采用选择和更新两个操作。

• 在选择操作中，信息素浓度越高的路径被选择的概率越大；
• 在更新操作中，路径上的信息素随蚂蚁的经过而增长，同时也随时间的推移而挥发。

通过不断的选择和更新操作，较好的解通过路径上的信息素得到加强，从而引导下一代蚂蚁向较优解邻域搜索使算法收敛，同时信息素的挥发增加了解的多样性，使得算法不易陷入局部最优

蚁群算法的参数设定

• 蚂蚁数量
  如果 m 值过大，会导致搜索过的路径上的信息素变化趋于平均，增加了寻找最短路径的时间成本；如果 m 值过小，导致最短路径过于早熟，降低了最优解的质量
• 信息素启发因子
  反映了蚂蚁在移动过程中积累的信息素在指导蚂蚁搜索中的相对重要程度，如果 α 值过大，蚂蚁选择以前搜索过路径的概率增大，使得搜索的随机性减弱；如果 α 值过小，等同于贪心算法，使得搜索过早陷入局部最优
  +期望值启发因子β
  反映蚂蚁搜索过程中先验性和确定性因素的重要程度，如果β值过大，会加快收敛速度，容易陷入局部最优；如果β值过小，容易陷入随机搜索，使得搜索时间增多，不易找到最优解
• 信息素挥发因子ρ
  反映信息素消失的速度，其大小直接关系到蚁群算法的全局搜索能力和收敛速度。
• 信息素强度Q
  表示蚂蚁循环一周时释放在路径上的信息素总量，其作用是充分利用全局信息反馈量，使算法在正反馈机制下以合理的速度搜索到全局最优解

粒子群算法

粒子群算法是一种基于群体协作的随机搜索算法。粒子群算法将问题空间的每个可能解类比为搜索空间中的一只鸟，称之为粒子，群体中每个粒子都有一个适应值，并且每个粒子知道自己的当前位置和目前为止发现的最好位置（即个体极值），每个粒子还知道目前为止整个群体中所有粒子发现的最好位置（即全局极值）

每个粒子根据自己的飞行经验和同伴的飞行经验，在搜索空间中以一定的速度飞行，通过粒子间的相互协作和信息共享，引导整个群体向最优解的方向移动，以迭代的方式进行搜索从而得到最优解

粒子主要通过以下三部分来更新速度：

• 粒子当前的速度；
• 粒子自身的飞行经验，即粒子的当前位置与自己最好位置之间的距离；
• 同伴的飞行经验，即粒子的当前位置与群体最好位置之间的距离。

例子算法的框架

算法：粒子群算法的一般框架
输入：问题模型，惯性权重因子 ω，学习因子 φ1 和 φ2
输出：最优解
       1. 设置种群规模为 m，初始化种群，设定每个粒子的随机位置和速度；
       2. 重复下述操作，直至满足终止条件：
           2.1 循环变量 i 从 1~n，对每个粒子执行下述操作：
                 2.1.1 计算粒子 i 的适应值；
                 2.1.2 如果粒子 i 的适应值比 pi 好，则更新当前的最好位置 pi；
                 2.1.3 如果粒子 i 的适应值比 gi好，则更新粒子群的最好位置 gi；
                 2.1.4 改变粒子 i 的速度和位置；
      3．输出粒子群的最好位置 g；

粒子群算法的参数设定

• 惯性权重因子 ω
  体现了当前速度对下一时刻速度的影响，使粒子具有扩展搜索空间的能力
• 最大速度 \(V_{max}\)
  如果当前粒子的某维速度超过 \(V_{max}\)，则将该维的速度调整为 \(V_{max}\) 。如果 \(V_{max}\) 过高，粒子可能会飞过最好解，如果 \(V_{max}\) 过低，粒子容易陷入局部最优
• 学习因子 φ1 和 φ2
  控制个体经验和同伴经验对下一时刻速度的影响
• 扰动因子 r1 和 r2
  引入扰动因子 r1 和 r2 是为了增加个体搜索和群体搜索的随机性和多样性

由于粒子群算法的收敛速度快，设置参数少，特有的记忆能力使粒子可以动态调整搜索策略，近年来受到学术界的广泛关注