深度学习入门第五章总结

目录

• 加法和乘法的反向传播
• 激活层函数的实现
  • Relu函数
  • sigmoid函数
  • Affine层
  • softmax函数

误差反向传播法还是很重要的。这一章节的内容比较细碎。因此我准备梳理一下。

在这本书的上一章中，我们介绍了利用数值微分来计算神经网络中的参数问题。本章节要使用误差反向传播。这两者的区别就是前者比较耗费时间。

数值微分：就是直接对函数式进行求偏导，一步到位。

反向传播的过程是对函数式进行拆分，倒着来。

grad是梯度的意思，我们使用数值微分（其实就是偏导数）求得结果后，将梯度*学习率就得到了变化量。让原来的值减去变化量就得到了新值。

network.params[key]-=learning*grad[key]

书上是以计算图的模式来写的。所谓的计算图，本人理解就是把数学公式拆成一步一步的。例如2+（53）就可以拆成 5 * 3，和2 15。反向传播是链式求偏导。

---

加法和乘法的反向传播#

加法求偏导就是1，也就是从上游传下来的导数不用发生任何变化。

乘法求偏导就是交换两个乘数。例如a*b,那么对a求偏导就是 b *导数。（乘数的翻转）

激活层函数的实现#

激活层位于神经元内部，也就是在神经元内部运行的函数。本章中使用了两种。分别是 Relu 函数以及Sigmoid函数。

Relu函数#

Relu函数的定义十分简单。

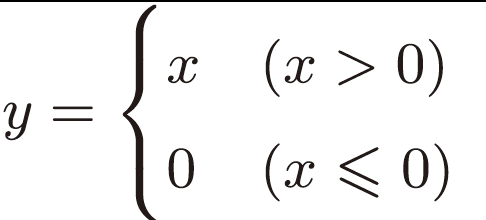
因此，对它的求导也十分的简单。

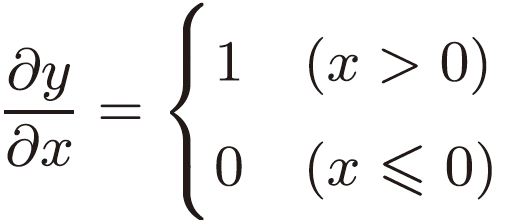
sigmoid函数#

x*(-1)再exp()一下，随后加上一，最后再取倒数。

Affine层#

这个层其实就是矩阵乘法。反向传播的话，就是乘上另一个的乘数的转置。到底是左乘还是右乘，取决于怎么方便乘。

softmax函数#

一般在分类的时候使用，公式很简单，分子是对数，分母是对数之和。

这个的反向传播需要和正确的数据相减。