纸稿草的 Iew_Trebla

8.1 T1

\(n = 40\)，考虑 meet in the middle，分成两个大小为 \(\dfrac{n}{2}\) 的集合 \(A, B\)，内部是好判断的，考虑如何合并。我们发现固定集合 \(A\) 后相当于在 \(B\) 中钦定一些 \(0, 1\)，剩下位任选，但只能做到 \(\mathcal{O}(3 ^ {\frac{n}{2}})\)，无法通过。

考虑特殊性质，只有限制二时，我们发现 \(A\) 到 \(B\) 只有必须选 \(0\) 的限制，高维前缀和即可。考虑拓展，我们发现 \(\neg y \to \neg x\) 的限制是好的，我们对 \(x \to y\) 的限制，\(x\) 向 \(y\) 连边，考虑保证没有 \(B\) 向 \(A\) 连的边。强连通分量缩点，则每个点内所选的数必须一样，形成 DAG 后，取拓扑序后 \(\frac{n}{2}\) 个点即可。复杂度 \(\mathcal{O}(2 ^ {\frac{n}{2}}(n + m))\)。

8.1 T2

\(m = \dfrac{n}{2}\)。考虑确定括号序列形态的情况，我们发现左右括号内部的贡献是确定的，一定是 \((m!) ^ 2 \dbinom{m}{2}\)。考虑两者之间的贡献，设 () 共 \(x\) 对，)( 共 \(y\) 对，则 \(x + y = m ^ 2\) 固定。我们发现可以预处理出 \(c\) 中 () 和 )( 对数从而计算出逆序对数，故答案只与 \(y\) 有关。具体地，答案为 \(C_m (m!) ^ 2 \dbinom{m}{2} + ((m - 1)!) ^ 2(Y(m ^ 2 - t) + (C_mm ^ 2 - Y)t)\)，其中 \(Y = \sum y\)，\(t\) 为当前字符串逆序对数，\(C\) 为卡塔兰数。考虑使用 BIT 在交换过程中维护原序列中 )( 的对数，使用 BIT 的 \(\mathcal{O}(n)\) 建树的科技即可做到 \(\mathcal{O}(n + q \log n)\)。事实上不需要 BIT，我们发现交换 \(l, r\) 只需考虑 \(l + 1, l + 2, \cdots, r - l\) 中的左，右括号数量，经过分讨易知改动量为 \(\pm (r - l)\)，可以做到 \(\mathcal{O}(n + q)\)。

熟知括号序列总数是卡塔兰数，我们只关心所有长度为 \(n\) 的括号序列的 \(\sum y\)。我们考虑第 \(i\) 个 ) 前有 \(j\) 个 ( 的方案数。考虑 dp，转化成网格图上的面积，枚举第一个 \(y = x\) 上的点，有 \(f_i = 2\sum\limits_{j = 1} ^ n f_{j - 1} g_{n - j} + \sum\limits_{j = 1} ^ n g_{j - 1}g_{n - j} j(n - j)\)，其中 \(g\) 为卡塔兰数，分治 MTT 可做到 \(\mathcal{O}(n \log ^ 2 n)\)。有三种优化方法：

1. OEIS 得 \(Y = (m + 1) \dbinom{2m - 1}{m} - 2 ^ {2m - 1}\)。
2. 生成函数硬推。
3. 我们考虑两对匹配的括号 \((a, b), (c, d)\)，我们发现 \([a, b]\) 与 \([c, d]\) 要么相离，要么包含。不妨 \(a < c\)，在 \(b < c\) 时，会形成 \((b, c)\) 一个 )( 对，若 \(b > d\)，则不会形成任何 )( 对。我们考虑对互相包含的匹配括号对计数，我们考虑枚举 \([a, b]\)，我们发现 \(s_as_{a + 1}\cdots s_b\) 是一个合法括号序列，故其中匹配的括号对数必为 \(\dfrac{b - a + 1}{2}\)。对于长度为 \(i\) 的匹配的括号对，它内部共 \(C_{\frac{i}{2} - 1}\) 中方案，考虑将其插入一个 \(n - i\) 长括号序列中，有总贡献为 \(\sum \limits_{i = 1} ^ {m - 1} (2(m - i - 1) + 1)iC_iC_{m - 1 - i}\)，\(\mathcal{O}(n)\) 计算即可。

P8339

考虑枚举同色的（钥匙，宝箱）对进行贡献计算。我们可以用类似括号序列匹配的方式进行钥匙与宝箱的匹配。具体地，我们认为一个（钥匙，宝箱）对合法当且仅当该钥匙到宝箱的路径上将该颜色的钥匙看作 (，该颜色的宝箱看作 )，形成一个合法括号序列，且该钥匙与该宝箱匹配。容易发现，这样将钥匙与宝箱匹配后，一个路径上能开的宝箱个数恰好是与遍历顺序同方向且被该路径包含的合法（钥匙，宝箱）对的钥匙到宝箱的路径的个数。这是因为我们遍历路径，用栈贪心匹配宝箱的结果恰好与我们的匹配方式等价，所以，在我们预处理出所有合法（钥匙，宝箱）对后可以在 dfs 序上二位数点做到 \(\mathcal{O}((n + m) \log n)\) 的复杂度。

考虑如何预处理，我们考虑对每种颜色建立虚树。我们将钥匙定为根进行搜索。搜索过程中，我们考虑用 dp 模拟括号匹配的过程。将钥匙视为 \(+1\)，宝箱视为 \(-1\)，搜索时遇到 dp 值为 \(0\) 的结点即可与根节点匹配，并立即返回即可（根据括号序列的匹配方式，只能与第一个 dp 值为 \(0\) 的宝箱匹配）。由于每种颜色的钥匙不超过 \(5\) 把，预处理复杂度为 \(\mathcal{O}(n \log n)\)，瓶颈在建立虚树。

QOJ9564

由于操作是循环的，我们考虑暴力模拟一轮操作，我们将 \((x, y)\) 向操作后的点 \((u, v)\) 连边，则会形成一颗内向基环树。发现一个不在环上的节点会在第它到最远子树内叶子的距离轮消失，我们可以 \(\mathcal{O}(nmk)\) 预处理出该值，我们称其为 \(tim_i\)。考虑每个合并会在什么时候发生，我们再暴力模拟一边第一轮操作，假设在 \(t\) 时刻，点 \(x\) 与点 \(y\) 合并，则我们发现在第 \(\min(tim_x, tim_y)\) 轮前，每轮内 \(x, y\) 都会在时间 \(t\) 合并，合并后将新节点的 \(tim\) 设为 \(\max(tim_x, tim_y)\) 即可。显然这样的合并就是所有的合并，由于至多有 \(nm\) 轮，开 \(nm\) 个 vector 记录该轮有哪些合并即可。复杂度 \(\mathcal{O}(nmk)\)。

CF1651F

首先我们可以发现怪物移动到下一座塔需要一秒钟的限制可以忽略，因为我们将第 \(i\) 座塔的时间整体减 \(i\) 不影响答案。我们考虑给在一次操作中清空的塔打上一个统一的时间戳，没有完全清空的塔至多有一个，可以独自建一段，单独处理。由于颜色段均摊，我们可以在查询时暴力遍历段，分段进行处理。现在问题变为了对一个区间 \([l, r]\)，清空后 \(t\) 时刻时的魔力值总和。

我们先考虑询问区间为 \([1, n]\) 的情形。考虑将塔按 \(\lceil \dfrac{c_i}{r_i} \rceil\) 排序，则回满的塔为一个前缀，没回满的为一个后缀，二分出分界点并写两颗线段树分别维护 \(\sum c_i\) 与 \(\sum r_i\) 即可。区间询问时，我们发现询问形如在线查询二位偏序，主席树维护即可。复杂度 \(\mathcal{O}((n + q) \log n)\)。

CF1647F

首先可以发现序列最大值必然是一个峰。考虑 dp，设 \(dp_{i, j, k}\) 为考虑 \(1, 2, \cdots, i\)，一个数列结尾为 \(j\)，另一个为 \(k\) 是否可行，我们这里只考虑不含最大值的数列递增的情形，转移是简单的。我们发现有 \(j = a_i\) 或 \(k = a_i\)，压掉一维。我们发现我们只需求另一维的最大值或最小值，再压掉一维。考虑从前往后 dp 一次再从后往前 dp 一次，枚举另一个峰 \(i\)，则将两侧的 dp 值合并，容易判断 \(i\) 是否可以做为峰，复杂度 \(\mathcal{O}(n)\)。

arc076_d

由于 Hall 定理，我们有左部点集合为 \(S\) 的二分图的最大匹配大小为 \(|S| - \max\limits_{T \subseteq S} (|T| - |N(T)|)\)，其中 \(N(T)\) 为 \(|T|\) 的邻点集合。考虑先对 \(l\) 排序，发现贡献形如二维偏序，扫描线即可。

CF954H

祖先到后代的路径是好处理的，我们只考虑 LCA 与路径两端都不重合的路径。记 \(p_x = \prod\limits_{i = 1} ^ x a_i\)，考虑深度为 \(x, y\)，LCA 深度为 \(z\) 的点对的贡献，则需要保证 \(\min(x, y) > z\)。我们发现这样的点对共有 \(p_{z - 1} \dfrac{p_{x - 1}}{p_z} \dfrac{p_{y - 1}}{p_z} \dbinom{a_z}{2} = \dfrac{p_{x - 1}p_{y - 1}a_z}{2p_z}\) 对，我们发现其关于 \(x, y, z\) 均独立。由于路径长度为 \(x + y - 2z\)，我们考虑记 \(f_{i, j} = \sum\limits_{x + y = i, \min(x, y) \ge j}p_{x - 1}p_{y - 1}\)，这可以通过枚举 \(x, y\) 再前缀和 \(\mathcal{O}(n ^ 2)\) 处理，再枚举 \(i, z\) 统计答案即可，复杂度 \(\mathcal{O}(n ^ 2)\)。

CF1720E

记矩阵中不同元素个数为 \(m\)。

• \(m \le k\) 时，答案为 \(k - m\)。
• \(m > k\) 时，容易发现答案 \(\le 2\)。我们设 \(L\) 为最大的长度使将 \((1, 1)\) 到 \((L, L)\) 的正方形变为同色后颜色数量仍 \(\ge k\)。此时我们考虑加入一个 \((m, m)\) 到 \((L + 1, L + 1)\) 的正方形，我们发现在 \(m\) 从 \(L + 1\) 遍历到 \(1\) 时，每次矩阵颜色数必定每次变化 \(\le 2\)，若 \(k\) 被取到则成立，否则取到 \(k - 1\)，让两个新矩形颜色不同即可。判断答案是否为 \(1\) 时枚举右上角与区间长度，在长度从小到大遍历的过程中考虑每种颜色的贡献即可。复杂度 \(\mathcal{O}(n ^ 3)\)。

QOJ971

考虑对序列扫描线，则我们只需要支持插入元素，删除元素与查询。我们发现一个点 \(b\) 的子树内有 \(a\) 当且仅当在区间 \([b, a]\)（\(b > a\) 时即为 \([a, b]\)）中 \(b\) 是时间戳最小的点。考虑对线段树上每个结点维护时间戳形成的左侧、右侧单调栈中数的和，单侧递归即可，复杂度 \(\mathcal{O}((n + m) \log ^ 2 n)\)，注意没有出现过的数时间戳视为 \(m + 1\)。

CF1413F

考虑取出直径 \(u, v\)，我们可以发现答案路径至少有一个端点是 \(u\) 或 \(v\)，下证明这一点。设 \(d(x, y)\) 为 \(x \to y\) 路径上 \(1\) 的个数 \(\bmod 2\) 的值，\(dis(u, v)\) 为 \(u \to v\) 的距离。

• \(d(u, v) = 0\)，答案即为 \(u \to v\)。

• \(d(u, v) = 1\)，设答案为 \(s \to t\)，若 \(\{s, t\} \bigcap \{u, v\} = \emptyset\)，我们讨论两种情况。

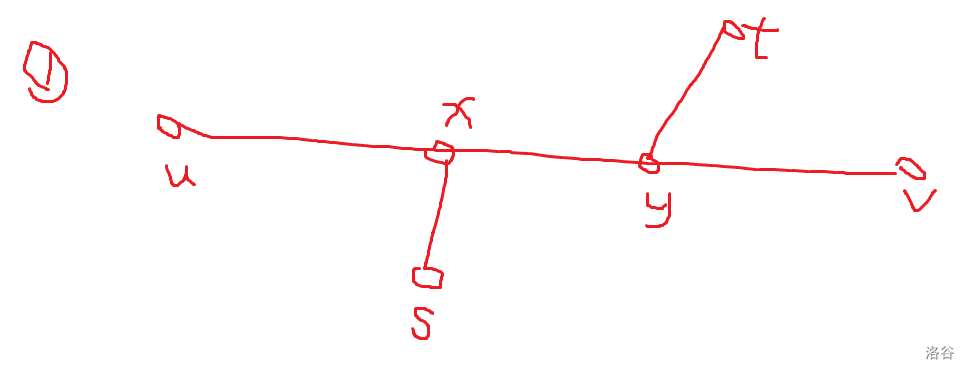
  1. \(s \to t\) 与 \(u \to v\) 有交。如图，我们设 \(s \to t\) 与 \(u \to v\) 交于 \(x, y\) 两点，其中 \(x\) 在 \(u, s\) 一侧，\(y\) 在 \(v, t\) 一侧。则我们有 \(dis(s, t) \leq dis(s, v)\)，\(dis(s, t) \le dis(u, t)\)。故 \(d(s, v) = d(u, t) = 1\)，我们有 \(d(u, v) \equiv d(u, y) + d(x, y) - d(x, y) \equiv d(u, t) + d(s, v) - d(s, t) \equiv 0 \pmod 2\)，矛盾。

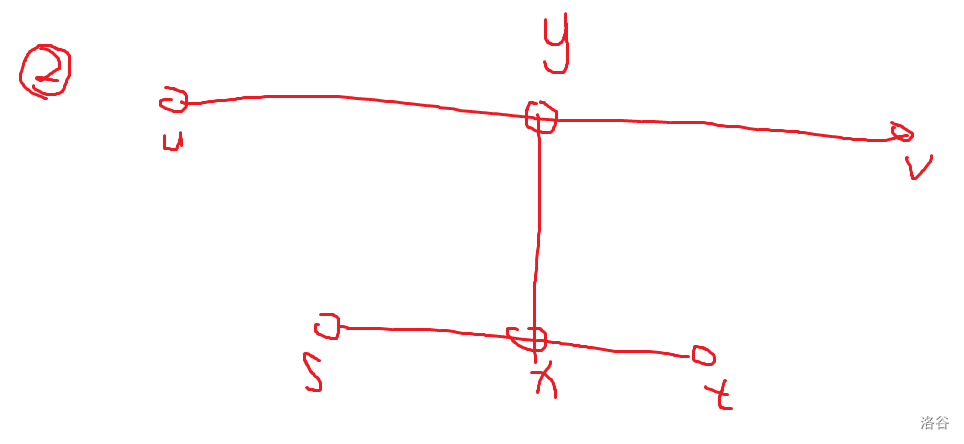
  2. \(s \to t\) 与 \(u \to v\)，设 \(s \to t\) 与 \(u \to v\) 之间的路径为 \(x \to y\)，则不妨 \(dis(s, u) \ge dis(s, t)\)，我们有 \(dis(t, v) + dis(s, u) \ge dis(u, v) + dis(s, t) \ge dis(s, u) + dis(s, t)\)，故 \(dis(t, v) \ge dis(s, t)\)，故 \(d(u, v) \equiv d(u, y) + d(y, v) \equiv d(u, s) + d(v, t) - d(s, t) \equiv 0 \pmod 2\)，矛盾。

结论证毕。则我们只需要以 \(u, v\) 为根，分别在 dfs 序上用线段树维护 \(d(u, i) = 0\) 和 \(d(v, i) = 0\) 的 \(i\) 的距离最大值，需要支持区间 \(0 \leftrightarrow 1\)，在线段树上分别维护区间内 \(d\) 为 \(0, 1\) 的距离最大值，修改即为交换，复杂度 \(\mathcal{O}(n \log n)\)。

agc017_d

考虑 SG 函数，我们发现一个公平组合游戏加上一个直接结束游戏的操作 SG 函数值会增加 \(1\)，故 \(f_u = \bigoplus\limits_{i} (f_i + 1)\)，复杂度 \(\mathcal{O}(n)\)。

8.6 T2

先考虑一个 \(\mathcal{O}(\operatorname{poly} n)\) 的 dp，考虑对深度序列进行 dp，我们有限制条件为 \(d_{i + 1} \le d_i + 1\)，\(d_a < \min_\limits{i = a + 1} ^ bd_i\)，我们发现可以把相交区间改成嵌套，建出树形结构后，我们发现子结点的限制一定比父节点更严，直接 dp 即可做到 \(\mathcal{O}(n ^ 2)\)，因为是树上背包。

CF1852D

考虑 dp，我们设 \(f_{i, j, 0/1}\) 表示填了 \((2, 1), (2, 2), \cdots, (2, i)\)，\((2, i)\) 填了 \(0\) 或 \(1\)，能否使相邻且字符不同的格子对数为 \(j\)。我们发现对于一个 \((i,0/1)\)，可行的 \(j\) 是一个区间去掉至多一个点，直接转移即可。

CF1310D

考虑给每个点随机赋权 \(0, 1\)，在二分图上跑 dp 即可。每次正确率为 \(2 ^ {-k}\)，随机 \(\mathcal{O}(2 ^ k) = 5000\) 次即可。复杂度 \(\mathcal{O}(2 ^ k k n ^ 2)\)。

P4516

设 \(f_{i, j, 0/1, 0/1}\) 表示 \(i\) 的子树内，放了 \(j\) 个监听设备，\(i\) 是否放置，是否被监视，书上背包转移即可，复杂度 \(\mathcal{O}(nk)\)。

CF2048F

对 \(b\) 建出笛卡尔树，设 \(f_{i, j}\) 为对于笛卡尔树上的第 \(i\) 个区间，操作 \(j\) 次后的区间最大值的最小值，注意到 \(j \le \log V\)，直接 dp 即可，复杂度 \(\mathcal{O}(n \log ^ 2 V)\)。

CF685C

先拆绝对值，二分答案，可以将 \(8\) 个限制写成形如 \(A \le x + y + z \le B\)，\(C \le x + y - z \le D\)，\(E \le x - y + z \le F\)，\(G \le -x + y + z \le H\) 的形式，后三式相加判断区间是否有交即可。复杂度 \(\mathcal{O}(n + \log V)\)。

CF1179D

我们发现对于点对 \((u, v)\) 以及他们的 LCA \(L\)，贡献为 \(\sum\limits_{i \in T_x, u \in T_i}(|T_i| - |T_j|)(n - |T_i|) + \sum\limits_{i \in T_y, v \in T_i}(|T_i| - |T_j|)(n - |T_i|) - |T_x||T_y|\)，其中 \(T_u\) 为 \(u\) 的子树，\(j\) 为 \(i\) 在 \(u\)（或 \(v\)） 的方向的子结点，\(x, y\) 为 \(L\) 在 \(u, v\) 方向的子节点。于是你可以先用 dp 算出 \(f_u = \max\limits_v (f_v + (|T_u| - |T_v|)(n - |T_u|))\)，表示 \(\max\limits_{v \in T_u} \sum\limits_{i \in T_u, v \in T_i}(|T_i| - |T_j|)(n - |T_i|)\)，再枚举 LCA，用斜率优化计算 \(\max\limits_{u, v \in ch_x} f_u + f_v - |T_u||T_v|\) 即可。

CF878C

如果 \(u\) 偏序（即每一维都大于）\(v\)，我们建 \(u \to v\) 的边。我们考虑用 set 维护强连通块。我们发现在可以 set 中查找有没有可以和新节点合并的强连通块，暴力合并即可，答案即为第一个强连通块的大小。由于每次至多增加一个强连通块，复杂度 \(\mathcal{O}(n \log n)\)。

uoj821

我们发现只需考虑前缀最大值（非严格），因为我们发现使用前缀最大值将序列分为若干段后每一段在归并排序的过程里不可能被分开或合并。所以我们可以不妨假设 \(a_i\) 递增。

由于限制为 \(|A_i| \neq \emptyset\)，我们考虑容斥。我们钦定 \(n - m\) 个集合为空集，设 \(i\) 的个数为 \(c_i\)，则方案数为 \(\prod\limits_{i = 1} ^ m \dbinom{m + c_i - 1}{c_i - 1}\)，答案即为 \(\sum\limits_{s = 1} ^ n \dbinom{n}{s} (-1) ^ {n - s} \left(\prod\limits_{i = 1} ^ m \dbinom{s + c_i - 1}{c_i - 1}\right)\) 我们发现不同的 \(c_i\) 只有 \(\mathcal{O}(\sqrt m)\) 个，直接计算复杂度即为 \(\mathcal{O}(n \sqrt m)\)。没有快速幂的 \(\log\) 是因为我们设 \(c_i = k\) 的 \(i\) 共有 \(t_k\) 个，\(\sum\limits_{t_k \ge 1}\log t_k = \sum\limits_{p \ge 0} \sum\limits_k [t_k \ge 2 ^ p] = \sum\limits_{p \ge 0} \sum\limits_k [\lfloor \dfrac{t_k}{2 ^ p} \rfloor \ge 1]\)，而 \(\sum\limits_k k \lfloor \dfrac{t_k}{2 ^ p} \rfloor \le \dfrac{m}{2 ^ p}\)，我们有 \(\sum\limits_{p \ge 0} \sum\limits_k \lfloor \dfrac{t_k}{2 ^ p} \rfloor \le \sum\limits_{p \ge 0} \sqrt{\dfrac{m}{2 ^ p}} = \mathcal{O}(\sqrt m)\)。

QOJ8717

考虑方案数其实是卷积的形式，我们设 \(f_i(x) = \sum\limits_{j = 0} ^ m p_{i, j} x ^ j\)，我们预处理出 \(f_i\) 的前缀积 \(pre_i\) 与前缀积的逆 \(ipre_i\)，再设 \(g(x) = \sum\limits_{i = 0} ^ mb_i x ^ {m - i}\)，我们所求即为 \(pre_ripre_{l - 1}g\)，预处理 \(pre_ig\) 即可。但有一个问题，\(f_i\) 不一定有逆，于是记录末尾 \(0\) 个数即可。复杂度 \(\mathcal{O}(n m \log m + qm)\)，暴力多项式乘法是 \(\mathcal{O}(nm ^ 2 + qm)\) 的。

8.8 T3

https://www.cnblogs.com/aemmprty/p/19029184

AT_snuke21_e

\(n\) 阶竞赛图强连通分量计数：枚举分界点。

\[\sum_{i = 1} ^ n \dbinom{n}{i}2 ^ {\binom{n - i}{2} + \binom{i}{2}} \]

arc163_d

还是考虑在分界点计数。我们发现若前 \(k\) 个数和为 \(S\)，则前 \(k\) 个数与后 \(k\) 个数所形成的顺序对数为 \(\dfrac{k(2n - k + 1)}{2} - S\)。考虑 dp，设 \(f_{i, j, k}\) 为前 \(i\) 个数，选了 \(j\) 个，和为 \(k\) 的方案数，容易 \(\mathcal{O}(n ^ 4)\) 求出。然后枚举分界点与其中一边的和即可。此时内部的方案数为 \(\dbinom{\binom{i}{2} + \binom{n - i}{2}}j{}\)，其中 \(i\) 为左边的点数，\(j\) 为两侧之间的顺序对数。

P10299

首先先考虑把所有数减去平均值再乘上 \(2n\)，将条件转化为连通块总和为 \(0\)。

我们从左往右考虑，将连通块在此格结束的格子称为 x，不确定连通块是否延伸的称为 o（即我们允许一个本应为 x 的格被称作 o），则一列共有 xx，xo，ox，oo 四种状态。我们考虑对其进行 dp，并在连通块的结束位置计算贡献。设前 \(i\) 列以 xx，xo，ox，oo 结尾的最多连通块数量分别对应 \(f_{i, 0/1/2/3}\)。记 \(pre_{i, j}\) 为第 \(i\) 行前 \(j\) 列的和，考虑转移：

1. oo 的转移：由于 oo 情况没有连通块结束，导致没有贡献产生，故第 \(i\) 列结尾为 oo 的答案是第 \(i - 1\) 列以所有情况结尾的所有 dp 值的 \(\max\)，即 \(f_{i, 3} = \max\{f_{i - 1, 0}, f_{i - 1, 1}, f_{i - 1, 2}, f_{i - 1, 3}\}\)。

2. xx 的转移：首先可以发现 xx 只会在 \(pre_{0, i} + pre_{1, i} = 0\) 时出现。此时考虑完该列 oo，ox，xo 的转移后我们发现都可以将原有的分割方式在此处新增一个连通块，故我们有 \(f_{i, 0} = \max\{f_{i, 1}, f_{i, 2}, f_{i, 3}\} + 1\)。

3. xo 的转移：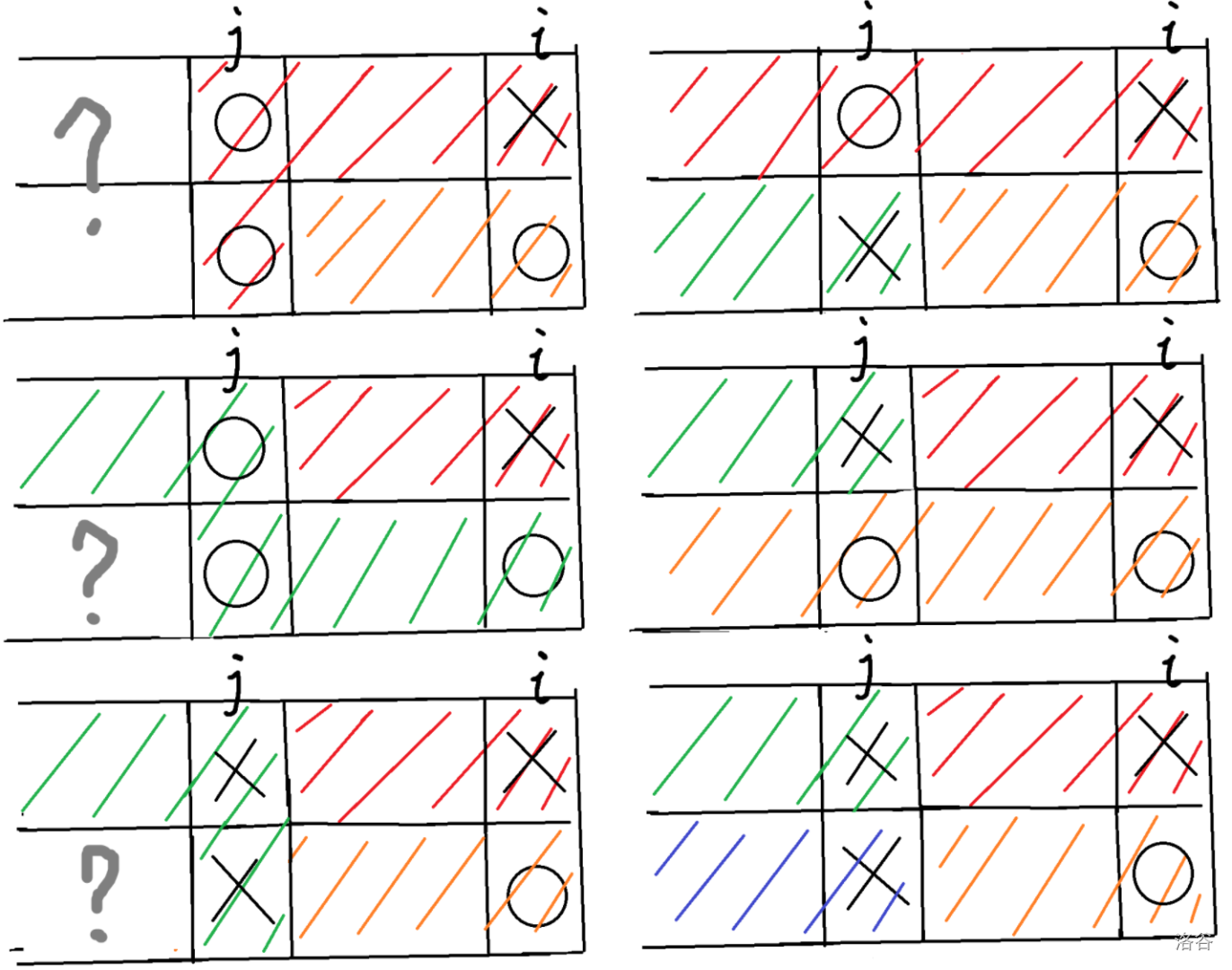

   

   我们考虑找到一个位置 \(j\)，满足确定了第 \(j\) 列的状态我们就能保证新加入的连通块总和为 \(0\)。我们发现有以下两种条件可保证这一点。

   • 第 \(j\) 列由两个在第 \(i\) 列前结束的连通块占据（对应第一行和第三行四种情况），要求为 \(pre_{0, i} + pre_{1, j} = 0\)。
   • 新连通块恰好占据 \((0, j + 1), (0, j + 2), \cdots, (0, i)\)，要求为 \(pre_{0, i} = pre_{0, j}\)。

   我们要找到满足该条件最大的 \(j\)，以保证第 \(j + 1\) 到 \(i - 1\) 列间没有贡献产生。在第一种情况中我们要求该连通块必须占据 \((0, j + 1), (0, j + 2), \cdots, (0, i)\) 且不能占据 \((1, j + 1), (1, j + 2), \cdots, (1, i)\)，在第两种情况中我们均要求 \((1, j + 1), (1, j + 2), \cdots, (1, i)\) 在同一个连通块中。由于这两个条件，我们容易发现第 \(j + 1\) 到第 \(i\) 列不会产生贡献。考虑分类讨论：

   • 若两种条件均成立（对应第三行两幅图），则第 \(j\) 列状态为 xx，故贡献为 \(f_{j, 0} + 1\)。
   • 若仅有第一个条件成立（对应第一行两幅图），则我们有 \((0,j)\) 在新连通块中，讨论 \((1, j)\) 是否在新连通块中，我们有贡献为 \(\max(f_{j, 1}, f_{j, 3}) + 1\)。
   • 若仅有第二个条件成立（对应第二行两幅图），则我们有 \((1, j)\) 与 \((1, i)\) 在同一个连通块中。讨论 \((0, j)\) 是否在该连通块中，我们有贡献为 \(\max(f_{j, 2}, f_{j, 3}) + 1\)。

4. ox 的转移：与 xo 同理。

我们使用 map 或哈希表找到满足 \(pre_{j, 0} = pre_{i, 0}\) 和 \(pre_{j, 1} = -pre_{i, 0}\) 的 \(j\) 的 dp 值的最大值即可完成转移，复杂度为 \(\mathcal{O}(n)\) 或 \(\mathcal{O}(n \log n)\)。

  n = read();
  F(i, 0, 1) F(j, 1, n) sum += (a[i][j] = read());
  F(i, 0, 1) F(j, 1, n) a[i][j] = 2 * n * a[i][j] - sum + a[i][j - 1];
  memset(dp, ~0x3f, sizeof dp), dp[0][0] = 0;
  auto get = [&](int x, int y, int z) {
    if (mp[x][y].find(z) != mp[x][y].end()) return mp[x][y][z];
    return -INF;
  };
  mp[0][0][0] = mp[1][0][0] = 0;
  F(i, 1, n) {
    F(j, 0, 3) Fmax(dp[i][3], dp[i - 1][j]);
    dp[i][1] = max(get(0, 0, a[0][i]), get(1, 1, -a[0][i])) + 1;
    dp[i][2] = max(get(1, 0, a[1][i]), get(0, 1, -a[1][i])) + 1;
    if (a[0][i] + a[1][i] == 0) F(j, 1, 3) Fmax(dp[i][0], dp[i][j] + 1);
    F(j, 0, 1) {
      Fmax(mp[j][0][a[j][i]], max({dp[i][0], dp[i][1 + j], dp[i][3]}));
      Fmax(mp[j][1][a[j][i]], max(dp[i][1 + j], dp[i][3]));
    }
  }
  cout << dp[n][0] << '\n';

P1963

首先容易注意到满足条件的 \(T_i\) 恰为 \(i - D_i, i + D_i\) 两个（\(\bmod\ n\) 意义下）。考虑 \(i - D_i\) 向 \(i + D_i\) 连边。若存在一个连通块 \(|V| > |E|\) 则不成立，否则由于共有 \(n\) 条边，每个连通块均为基环树。树上的边显然只能选子节点，环上的边有两种选择，分讨贪心即可，复杂度 \(\mathcal{O}(n)\)。

CF1819D

我们考虑枚举最后一次清空的时间 \(t\)。则若 \(t + 1\) 到 \(n\) 有 \(0\)，答案为 \(m\)，否则答案为 \(k_{t + 1} + k_{t + 2} + \cdots +k_n\)。记 \(f_i\) 为 \(1, 2, \cdots, i\) 能否完全清空，记 \(lst_i\) 为上一个与 \(S_i\) 有交的集合位置，\(pre_i\) 为上一个 \(0\) 的位置，若没有则视为 \(0\)。考虑枚举上一次清空位置 \(k\) 进行转移：

• 对于 \(k \in [1, \max\limits_{j = 1} ^ {i - 1} lst_j)\)，我们发现在 \(k\) 清空后必然会在 \(i - 1\) 前再清空一次，故无法转移。
• 对于 \(k < lst_i\)，我们显然会在 \(i\) 及以前清空至少一次。
• 对于 \(k < pre_i\)，我们令 \(pre_i\) 位置的集合取 \(S_i\) 的任意一个元素，则必然会在 \(i\) 及以前清空。

故合法的转移点为 \([\max\limits_{j = 1} ^ {i - 1} lst_j, \max\{pre_i, lst_i\})\)，前缀和优化即可，复杂度 \(\mathcal{O}(n)\)。

agc030_d

记 \(f_{i, j}\) 为第 \(i\) 个位置和第 \(j\) 个位置形成逆序对的概率，每次交换 \(x, y\) 显然只有 \(\mathcal{O}(n)\) 个位置改变，即 \(f_{x/y, u} \leftarrow \dfrac{f_{x, u} + f_{y, u}}{2}\), \(f_{x, y} \leftarrow \dfrac{1}{2}\)。直接转移复杂度即为 \(\mathcal{O}(n(n + q))\)。

agc005_f

考虑分别对每个点计算贡献，我们设去掉第 \(u\) 个点后，树会分为大小为 \(sz_1, sz_2, \cdots, sz_m\) 的连通块，则点集大小为 \(k\) 时 \(u\) 的贡献为 \(\dbinom{n}{k} - \sum\limits_{i = 1} ^ m \dbinom{sz_i}{k}\)。我们设对所有的 \(u\)，形如 \(\dbinom{x}{k}\) 的贡献系数为 \(a_x\)，则 \(k\) 时答案为 \(\sum\limits_{x = 1} ^ n \dfrac{a_x x!}{k!(x - k)!} = \dfrac{1}{k!} \sum\limits_{x = 0} ^ {n - k} a_{x + k}(x + k)! \dfrac{1}{x!} = \dfrac{1}{k!} \sum\limits_{x = 0} ^ {n - k} f(n - x - k) g(x)\)，NTT 即可，复杂度 \(\mathcal{O}(n \log n)\)。

P4350

从大到小加边，维护 \(0, 2\) 度点个数，再用并查集维护环数即可。

arc019_d

枚举匹配位置，处理出每个点至少往左或往右移动多少，桶排序后贪心匹配即可。复杂度 \(\mathcal{O}(n ^ 2)\)。

CF1225F

容易发现答案为 \(n - \max dep_i\)，长剖后考虑操作短链长度次，先遍历轻子树，对于点 \(u\) 和它 dfs 序的上一个点 \(v\)，操作 \(dep_v - dep_u + 1\) 次即可。复杂度 \(\mathcal{O}(n)\)。

abc306_h

先考虑没有 = 怎么做，我们发现是经典的 DAG容斥。再考虑有 = 的情况，我们仍然设 \(f_S\) 为将 \(S\) 导出子图中边定向形成 DAG 的方案数。依然枚举入度为 \(0\) 的点集 \(T\)。设 \(T\) 的导出子图中连通块数为 \(sz_T\)，则由于 DAG 容斥结论，容斥系数为 \((-1) ^ {sz_T + 1}\)，复杂度 \(\mathcal{O}(3 ^ n)\)。

CF1299E

首先我们发现 \(\dfrac{n(n + 1)}{2} \equiv 1 \pmod {n - 1}\)，于是考虑询问所有大小为 \(n - 1\) 的点集，即可确定 \(1\) 和 \(n\) 的位置（此时我们可以任意钦定 \(1\) 和 \(n\) 的顺序，做完后比较字典序再确定是否需要 \(a_i \to n - a_i + 1\) 即可）。此后我们询问 \(1, p_k\) 即可确定 \(p_k \bmod 2\)。类似地，我们问出 \(2, n - 1, 3, n - 2, 4, n - 3\) 的位置（此处可以通过 \(\bmod \ 2\) 的值确定具体位置），以上共消耗 \(5n\) 次操作。

注意到 \(3 \times 5 \times 7 \times 8 = 840 > 800\)，我们考虑通过 CRT 确定每一个数。我们考虑构造 \(\bmod\ 3, 5, 7\) 互不相同的 \(2, 4, 6\) 元集。

• 询问 \(\{1, 2, p_k\}, \{1, 3, p_k\}\)，可在 \(n + \dfrac{2n}{3} = \dfrac{5n}{3}\) 次确定 \(p_k \bmod 3\)。

• 询问 \(\{1, 2, n - 1, n, p_k\}, \{1, 3, n - 1, n, p_k\}, \{1, 4, n - 1, n, p_k\}, \{2, 4, n - 1, n, p_k\}\)。

  可在 \(n + \dfrac{4n}{5} + \cdots + \dfrac{2n}{5} = \dfrac{14n}{5}\) 次确定 \(p_k \bmod 3\)。

• 询问 \(\{1, 2, 3, n - 3, n - 2, n - 1, p_k\}, \{1, 2, 4, n - 3, n - 2, n - 1, p_k\}, \{1, 3, 4, n - 3, n - 2, n - 1, p_k\}, \\ \{2, 3, 4, n - 3, n - 2, n - 1, p_k\}, \{2, 3, 4, n - 3, n - 2, n, p_k\}, \{2, 3, 4, n - 3, n - 1, n, p_k\}\)。

  可在 \(\dfrac{27n}{7}\) 次确定 \(p_k \bmod 7\)。

考虑倍增确定 \(\bmod \ 8\) 的值。按照奇偶性，若奇数则询问 \(\{1, 2, 4, p_k\}\)，偶数则询问 \(\{1, 2, 3, p_k\}\)，即可确定 \(p_k \bmod 4\)。我们发现 \(\{1, 2, 3, 4, n - 3, n - 2, n - 1, n\}\) 去掉 \(1, 2, 3, 4\) 中的一个元素后，\(\bmod \ 4\) 互不相同，讨论 \(\bmod \ 4\) 余数询问与其同余的七元集即可确定 \(p_k \bmod 8\) 的值。共消耗 \(2n\) 次操作。

综上，我们共使用 \((7 + \dfrac{5}{3} + \dfrac{14}{5} + \dfrac{20}{7})n = \dfrac{1609}{105}n\) 次询问，可以通过本题。

CF53E

考虑钦定集合 \(T\) 中的点度数为 \(1\)，将 \(T\) 中点删去后跑矩阵树定理即可 \(\mathcal{O}(n ^ 3)\) 求出剩余点导出子图中的生成树个数。再考虑将 \(T\) 中点挂在树上，贡献为 \(T\) 中每个点到 \(T\) 外的点边数的乘积。但这样会算重，于是高维前缀和进行容斥即可。复杂度 \(\mathcal{O}(n ^ 3 2 ^ n)\)。

P3643

我们考虑将 \(a_i\) 和 \(b_i + 1\) 一起离散化，将值域分成 \(\mathcal{O}(n)\) 个区间。我们容易发现 \([a_i, b_i]\) 一定是若干个整区间的并。考虑 dp，记 \(f_{i, j, k}\) 表示前 \(i\) 个学校，第 \(i\) 个学校的参赛划艇数量在第 \(j\) 个区间中，且共 \(k\) 个学校的参赛划艇数量在第 \(j\) 的区间中的方案数，转移系数为 \(\dfrac{(k - 1)!(len_j - k + 1)!}{k!(len_j - k)!}\)，前缀和优化即可，复杂度 \(\mathcal{O}(n ^ 3)\)。

CF1239E

首先显然可以注意到 \(a_{1, i}\) 递增，\(a_{2, i}\) 递减。其次，我们设 \(w_i = \sum\limits_{j = 1} ^ i a_{1, j} + \sum\limits_{j = i} ^ n a_{2, j}\)，我们发现 \(w_{i + 1} - w_i = a_{1, i + 1} - a_{2, i}\) 递增，故最大值必为 \(w_1\) 或 \(w_n\)。由于对称性，不妨 \(a_{1, 1}\) 最小。由于必定经过 \(a_{2, n}\)，我们容易说明 \(a_{2, n}\) 必取次小值。考虑 dp，设 \(f_{i, j, k}\) 为前 \(i\) 个数，第一行选了 \(j\) 个，总和为 \(k\) 是否可行，复杂度 \(\mathcal{O}(n ^ 3V)\)，可以除 \(64\)。

abc134_f

考虑每个元素的贡献，若是绝对值中较小的则为 \(-x\)，否则为 \(x\)。考虑 dp，设 \(f_{i, j, k}\) 表示考虑 \(1, 2, \cdots, i\)，目前总贡献为 \(j\)，\(p_1, p_2, \cdots, p_i\) 中有 \(k\) 个元素不在 \(1, 2, \cdots, i\) 中的贡献。考虑转移：

• 贡献为 \(2i\)，\(f_{i, j, k} \leftarrow f_{i - 1, j - 2i, k + 1} \times (k + 1) ^ 2\)。
• 贡献为 \(0\)，\(f_{i, j, k} \leftarrow f_{i - 1, j, k} \times(2k + 1)\)。（\(+1\) 是因为存在 \(p_i = i\) 的情况）。
• 贡献为 \(-2i\)，\(f_{i, j, k} \leftarrow f_{i - 1, j + 2i, k - 1}\)。

直接转移即可，复杂度 \(\mathcal{O}(n ^ 4)\)。

CF1542E2

首先容易想到枚举 lcp，设 \(lcp(p, q) = k\)，则显然原问题可以转化为长度为 \(n - k\) 且要求 \(p_1 < q_1\) 的子问题。枚举 \(q_1 - p_1\)，则只需考虑后 \(n - k - 1\) 个元素的逆序对数之差。考虑将 \(p, q\) 同时 dp，设 \(f_{i, j}\) 为长度为 \(i\)，\(p\) 逆序对数比 \(q\) 多 \(j\) 的方案数。转移直接枚举 \(p, q\) 中 \(i\) 的位置，可得 \(f_{i, j} = \sum\limits_{k = -i} ^ i(i - |k|)f_{i - 1, j + k}\)，拆绝对之后前缀和优化即可，复杂度 \(\mathcal{O}(n ^ 3)\)。

CF1580B

显然考虑笛卡尔树，我们发现一个数是好数当且仅当其在笛卡尔树中深度为 \(m\)。考虑 dp，设 \(f_{i, j, k}\) 为长度为 \(i\) 的排列，笛卡尔树中深度为 \(j\) 的结点有 \(k\) 个的方案数，转移枚举最大值位置即可，具体地，\(f_{i, 0, 1} = i!\)，\(f_{i, j, k} = \sum\limits_{x = 0} ^ {i - 1}\sum\limits_{y = 0} ^ k f_{x, j - 1, y}f_{i - x - 1, j - 1, k - y} \dbinom{i}{x}\)，直接转移复杂度为 \(\mathcal{O}(n ^ 5)\)，不知道为什么能过 \(n = 100\)。

P5470

考虑模拟费用流。考虑建图，我们发现 \(a_i, b_i\) 同时选不太好刻画，于是考虑刻画只选 \(a_i\) 不选 \(b_i\) 的情况（显然与只选 \(b_i\) 不选 \(a_i\) 出现次数相同），即限制其至多出现 \(K - L\) 次。我们将这种情况视为选了 \(a_i\) 后更换位置选择了 \(b_j\)。考虑先拆点，\(S\) 向 \(1, 2, \cdots, n\) 连容量为 \(1\)，费用为 \(a_i\) 的边，\(1', 2', \cdots, n'\) 向 \(T\) 连容量为 \(1\)，费用为 \(b_i\) 的边，分别表示选择了 \(a_i, b_i\)。对于都选，即不更换位置的情况，我们 \(i\) 向 \(i'\) 连容量为 \(1\)，费用为 \(0\) 的边。对于更换位置的情况，我们新建两个点 \(X, Y\)，\(i\) 向 \(X\)，\(Y\) 向 \(i'\) 连容量为 \(1\)，费用为 \(0\) 的边，再 \(X\) 向 \(Y\) 连容量为 \(K - L\)，费用为 \(0\) 的边即可。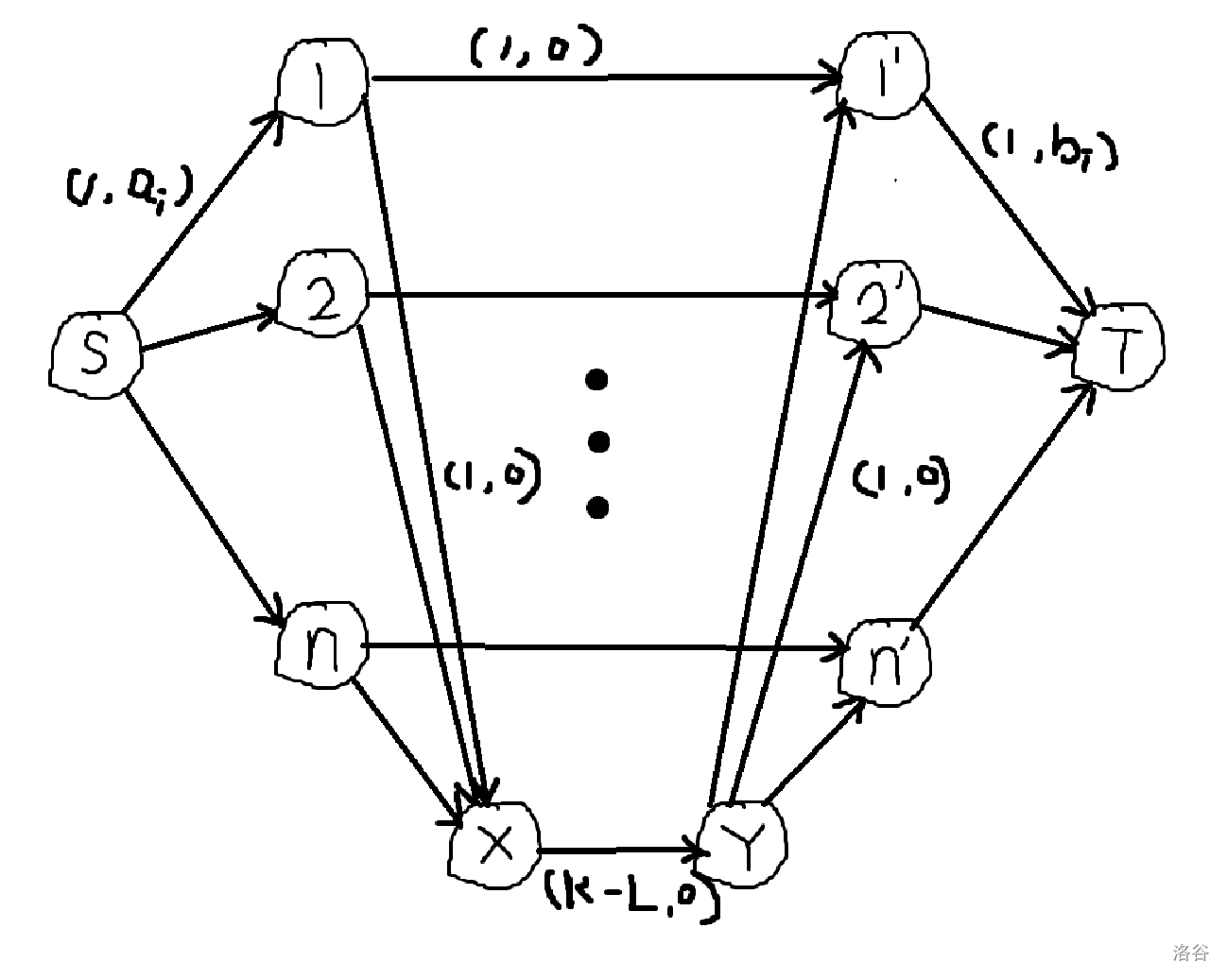

我们发现去掉 \(S, T, X, Y\) 四个点及其连出的边，剩余的边仅会构成 \(i \to i'\) 这 \(n\) 个大小为 \(2\) 的弱连通块，于是维护关键点之间只经过非关键点的最长路，增广 \(k\) 次即可，复杂度 \(\mathcal{O}(n \log n)\)，具体路径如下。

• \(S \to X:S \to i \to X\)。
• \(S \to Y:S \to i \to i' \to Y\)。
• \(S \to T:S \to i \to i' \to T\)。
• \(X \to T:X \to i \to i' \to T\)。
• \(Y \to T:Y \to i' \to T\)。
• \(X \to Y:X \to Y, X \to i \to i' \to Y\)。

容易发现不会存在 \(Y \to X\) 的情况。开 \(6\) 个堆维护会比 set 常数小非常多，不合法的查询时判断即可，不用删除。