ARTS - No.1

A

环形链表相交结点查找(LeetCode No.142)

给出类似如下的链表，返回相交的结点，即结点2

这是一个神奇的算法，使用的方法是快慢指针。具体步骤如下:

1. 定义2个指针pFast和pSlow，pFast每次迭代2个结点，pSlow每次迭代1个结点，直到pFast和pSlow相遇;

2. 不改变pSlow；重新定位pFast到链表头，这次pFast每次迭代1个结点，相当于另一个“pSlow”;

3. pFast，pSlow每次都迭代1个结点，直到pFast和pSlow相遇，此时相遇的结点就是相交的节点。

推导

神奇的过程，在给出代码前先分析一下。

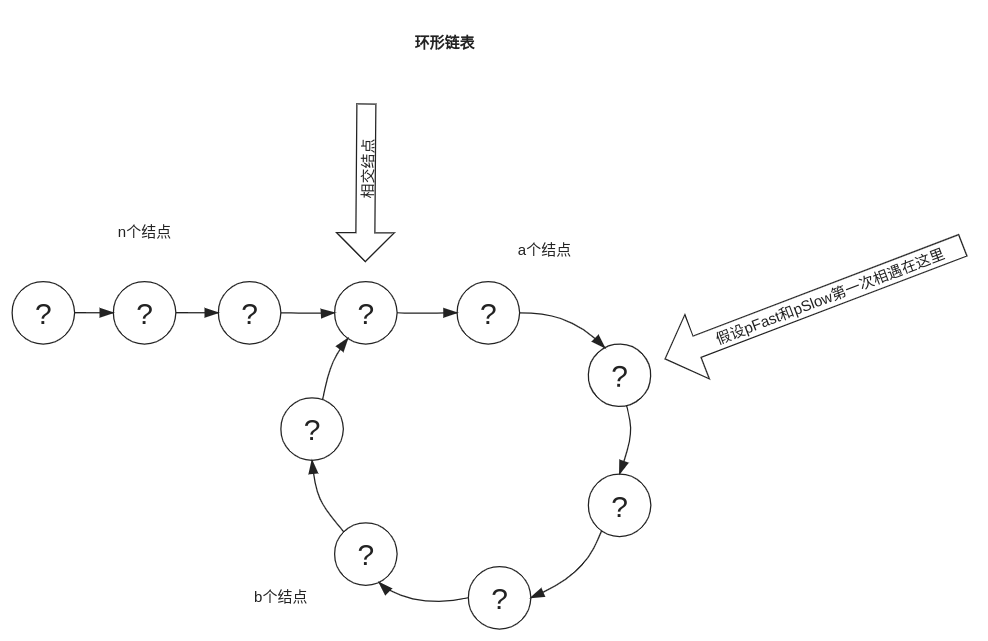
假设相交结点之前有n个结点(不包含相交结点)，相交结点到2个指针相遇结点共a个结点和b个结点。

到相遇结点处，pSlow走过的结点有n + a个，记住pSlow的位置。

然后pFast重新定位到链表头，并开始以步长1开始迭代，那么下一次pFast和pSlow相遇的地方是哪里呢？

就是相交结点啦！

为什么？其实很简单，首先，这个算法能求出相交结点，那么，假如pFast和pSlow没有在相交结点处相遇，注意这时候pFast的迭代步长是1，也就是说，这2个指针速度相同，它们就再也不会相遇了！

哈哈，开个玩笑，虽然道理是这样，但是正常的推导还是要有的。

假设pSlow在相遇前会转上j圈，再次相遇的位置在第n + a + c个结点处，那么pSlow走过的结点有j(a+b) + c个，pFast有n + a + c个。现在j(a+b) + c = n + a + c，得到n = (j-1)(a+b) + b。

这个(j-1)(a+b)代表pSlow转圈圈走过的节点数，它转了这么多圈以后，位置还是在第一次相遇的结点，然后它再走b个结点，就相当于走了(j-1)(a+b) + b个结点，也就是n个结点，这时候pFast也走了n个结点，所以它们就再次相遇了，相遇的位置就是相交结点.。

另一个思路

嗯……我还想再给一个骚操作：引用计数

在Python语言中，每个对象(obj)都有一个引用计数，可以用sys.getrefcount(obj)获取，环形链表的结点被另外2个结点引用，引用计数会更高，用这个特性来判断。

当然这么做是有限制条件的，如果结点被别的程序引用，引用计数改变，可能会判断错误，所以并不实用。用这个办法做题算是投机取巧了，就当开拓一下思路吧。

Python引用计数解法

R

Teach Yourself Programming in Ten Years

这篇文章的作者Peter Norvig是计算机科学家，Google 的研究总监。这个大佬的主页 http://www.norvig.com/ 真是出奇的简约……不过上面有好多值得一读的文章，《Teach Yourself Programming in Ten Years》就是其中之一。

我尝试了一下上面的中文翻译链接，貌似被墙了。实在看不懂英语的可以到这里看： https://www.jianshu.com/p/131b900931ac ，不过我个人还是建议阅读原文。

这是一篇完全反现代社会的文章，我觉得如果它改名成Teach Yourself Programming in Ten Minutes，阅读量可以翻倍;-)

内中详情请细品，我在这里就不啰嗦了，也吐不出什么良言金句来，大佬说得很明白了。

T

Python获取26个英文字母

import string

string.ascii_uppercase  # 获取26个大写字母
string.ascii_lowercase  # 获取26个小写字母
string.ascii_letters  # 获取26个小写字母和26个大写字母

>>> import string
>>> string.ascii_uppercase
'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
>>> string.ascii_lowercase
'abcdefghijklmnopqrstuvwxyz'
>>> string.ascii_letters
'abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ'

还有一些有趣的方法，详细内容查看官方文档。

S

优秀的代码和优秀的程序员

不可以小看编程，程序不是实现功能就够了，还需要考虑很多事情

• 泛型编程
• 逻辑是否清晰，易于理解
• 功能是否明确，不过分耦合
• 抽象层级是否合适

多想一想别的解法，多问一下为什么是这样而不是那样。