【计算机数学】DICE GAME

一、实验项目描述：

In this series of three programming tasks, we will implement together a program that will play optimally in a tricky dice game! Your program will be given a list of dices and will decide who chooses the dice first (you or your opponent).

When the dices are chosen, we will simulate 10000 throws. Each time your number is greater, you get $1 from your opponent. Conversely, each time your number is smaller, you pay $1 to your opponent.

Your ultimate goal is to implement a program that always wins in such a simulation.

1. First Task: Compare Two Dices

Implement a function that takes two dices as input and computes two values: the first value is the number of times the first dice wins (out of all possible 36 choices), the second value is the number of times the second dice wins. We say that a dice wins if the number on it is greater than the number on the other dice.

To debug your implementation, use the following test cases:

Sample 1

Input: dice1 = [1, 2, 3, 4, 5, 6], dice2 = [1, 2, 3, 4, 5, 6]

Output: (15, 15)

Sample 2

Input: dice1 = [1, 1, 6, 6, 8, 8], dice2 = [2, 2, 4, 4, 9, 9]

Output: (16, 20)

2. Second Task: Is there the Best Dice?

Now, your goal is to check whether among the three given dices there is one that is better than the remaining two dices.

Implement a function that takes a list of dices and checks whether there is dice (in this list) that is better than all other dices. We say that a dice is better than another one, if it wins more frequently (that is, out of all 36 possibilities, it wins in a cases, while the second one wins in b cases, and a>b). If there is such a dice, return its (0-based) index. Otherwise, return -1.

Use the following datasets for debugging:

Sample 1

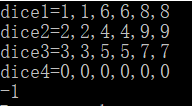
Input: [[1, 1, 6, 6, 8, 8], [2, 2, 4, 4, 9, 9], [3, 3, 5, 5, 7, 7]]

Output: -1

Sample 2

Input: [[1, 1, 2, 4, 5, 7], [1, 2, 2, 3, 4, 7], [1, 2, 3, 4, 5, 6]]

Output: 2

Sample 3

Input: [[3, 3, 3, 3, 3, 3], [6, 6, 2, 2, 2, 2], [4, 4, 4, 4, 0, 0], [5, 5, 5, 1, 1, 1]]

Output: -1

3. Third Task: Implement a Strategy

You are now ready to play!

Implement a function that takes a list of dices (possibly more than three) and returns a strategy. The strategy is a dictionary:

If, after analyzing the given list of dices, you decide to choose a dice first, set strategy["choose_first"] to True and set strategy["first_dice"] to be the (0-based) index of the dice you would like to choose

If you would like to be the second one to choose a dice, set strategy["choose_first"] to False. Then, specify, for each dice that your opponent may take, the dice that you would take in return. Namely, for each i from 0 to len(dices)-1, set strategy[i] to an index j of the dice that you would take if the opponent takes the i-th dice first.

Use the following datasets for debugging:

Sample 1

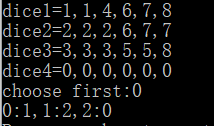
Input: [[1, 1, 4, 6, 7, 8], [2, 2, 2, 6, 7, 7], [3, 3, 3, 5, 5, 8]]

Output: {'choose_first': False, 0: 1, 1: 2, 2: 0}

Sample 2

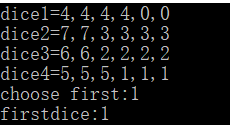
Input: [[4, 4, 4, 4, 0, 0], [7, 7, 3, 3, 3, 3], [6, 6, 2, 2, 2, 2], [5, 5, 5, 1, 1, 1]]

Output: {'choose_first': True, 'first_dice': 1}

Note that your answers do not have to coincide with the answers above. First, the order of elements does not matter in the dictionary. Second, the dictionary might contain extra information that is not required in the statement of the problem. For example, {0: 3, 'first_dice': 1, 'choose_first': True} is also a correct output in Sample 2.

Answers：

1. First Task: Compare Two Dices

#include <stdio.h>
int main()
{
    int a[6],b[6],c,d;
    printf("dice1=");
    scanf("%d,%d,%d,%d,%d,%d",&a[0],&a[1],&a[2],&a[3],&a[4],&a[5]);
    printf("dice2=");
    scanf("%d,%d,%d,%d,%d,%d",&b[0],&b[1],&b[2],&b[3],&b[4],&b[5]);
    int i,j,m=0,n=0;
    for(i=0;i<6;i++)
    {
        for(j=0;j<6;j++)
        {
            if(a[i]<b[j])
            {
                m++;
            }
            else if(a[i]>b[j])
            {
                n++;
            }
        }
    }
    printf("%d,%d",n,m);
    return 0;
}

2. Second Task: Is there the Best Dice?

#include<stdio.h>
int compare(int a[],int b[])
{
    int m=0,n=0,i,j;
    for(i=0;i<6;i++)
    {
        for(j=0;j<6;j++)
        {
            if(a[i]<b[j])
            {
                m++;
            }
            else if(a[i]>b[j])
            {
                n++;
            }
        }
    }
    if(m<n)
    {
        return 0;
    }
    if(m>n)
    {
        return 1;
    }
    else
    {
        return 2;
    }
}
int main()
{
    int a[6],b[6],c[6],d[6];
    printf("dice1=");
    scanf("%d,%d,%d,%d,%d,%d",&a[0],&a[1],&a[2],&a[3],&a[4],&a[5]);
    printf("dice2=");
    scanf("%d,%d,%d,%d,%d,%d",&b[0],&b[1],&b[2],&b[3],&b[4],&b[5]);
    printf("dice3=");
    scanf("%d,%d,%d,%d,%d,%d",&c[0],&c[1],&c[2],&c[3],&c[4],&c[5]);
    printf("dice4=");
    scanf("%d,%d,%d,%d,%d,%d",&d[0],&d[1],&d[2],&d[3],&d[4],&d[5]);
    int m,n,o,p,q,r;
    m=compare(a,b);
    n=compare(a,c);
    o=compare(a,d);
    p=compare(b,c);
    q=compare(b,d);
    r=compare(c,d);
    if(m==0&&n==0&&o==0)
    {
        printf("0\n");
    }
    else if(m==1&&p==0&&q==0)
    {
        printf("1\n");
    }
    else if(n==1&&p==1&&q==0)
    {
        printf("2\n");
    }
    else if(o==1&&q==1&&r==1)
    {
        printf("3\n");
    }
    else 
    {
        printf("-1\n");
    }
    return 0;
}

 

 

 

 

 

 

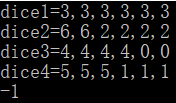
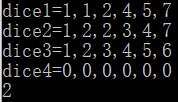
3. Third Task: Implement a Strategy

#include<stdio.h>
int compare(int a[],int b[])
{
    int m=0,n=0,i,j;
    for(i=0;i<6;i++)
    {
        for(j=0;j<6;j++)
        {
            if(a[i]<b[j])
            {
                m++;
            }
            else if(a[i]>b[j])
            {
                n++;
            }
        }
    }
    if(m<n)
    {
        return 0;
    }
    if(m>n)
    {
        return 1;
    }
    else
    {
        return 2;
    }
}
int main()
{
    int a[6],b[6],c[6],d[6],e,f;
    printf("dice1=");
    scanf("%d,%d,%d,%d,%d,%d",&a[0],&a[1],&a[2],&a[3],&a[4],&a[5]);
    printf("dice2=");
    scanf("%d,%d,%d,%d,%d,%d",&b[0],&b[1],&b[2],&b[3],&b[4],&b[5]);
    printf("dice3=");
    scanf("%d,%d,%d,%d,%d,%d",&c[0],&c[1],&c[2],&c[3],&c[4],&c[5]);
    printf("dice4=");
    scanf("%d,%d,%d,%d,%d,%d",&d[0],&d[1],&d[2],&d[3],&d[4],&d[5]);
    printf("choose first:");
    scanf("%d",&e);
    switch(e)
    {
        case 1:
        {
            int m,n,o,p,q,r;
            m=compare(a,b);
            n=compare(a,c);
            o=compare(a,d);
            p=compare(b,c);
            q=compare(b,d);
            r=compare(c,d);
            if(m==0&&n==0&&o==0)
            {
                printf("firstdice:0\n");
            }
            else if(m==1&&p==0&&q==0)
            {
                printf("firstdice:1\n");
            }
            else if(n==1&&p==1&&q==0)
            {
                printf("firstdice:2\n");
            }
            else if(o==1&&q==1&&r==1)
            {
                printf("firstdice:3\n");
            }
            else 
            {
                printf("firstdice:-1\n");
            }
            break;
        }
        case 0:
        {
            printf("0:");
            f=compare(a,b);
            if(f==1)
            {
                printf("1");
            }
            f=compare(a,c);
            if(f==1)
            {
                printf("2");
            }
            printf(",");
            printf("1:");
            f=compare(b,c);
            if(f==1)
            {
            printf("2");
            }
            f=compare(b,a);
            if(f==1)
            {
                printf("0");
            }
            printf(",");
            printf("2:");
            f=compare(c,a);
            if(f==1)
            {
                printf("0");
            }
            f=compare(c,b);
            if(f==1)
            {
                printf("1");
            }
            printf("\n");
            break;
        }
        default:break;
    }
    return 0;
}

 

Summary：

骰子游戏说明寻找最优解的过程是一个把所有解进行循环比较的过程，如果通过比较后有一个解比其他解都要优，就能选出最优解，如果每一个解都能找到一个解比它更优，那就不存在最优解，哪个解更优是相对的。