2017-2018 ACM-ICPC East Central North America Regional Contest (ECNA 2017) B-Caters 题解
Problem B Craters
题目描述
给我\(n\)个圆的半径和\(x\)和\(y\)的坐标,同时我需要在这个圆的周围拓宽十米,我们要做的事求出这\(n\)个圆组成的最大凸包的周长。
笔者想法
有点像那个经典求带圆面积的题信用卡凸包,你可以看一下这道题,或许对你有帮助。和这道题不同的是本题中圆的半径不是固定的,这样我们就用不了那个很美好的性质了。我的队友在看到这个题的时候发现这道题的\(n\)非常小,在200以内,所以他说能不能把一个圆细分成很多个点,然后按照普通凸包的做法来做。当时我否定了这个想法,口算了一下为了达到10-6的精度可能需要在每个圆上分特别特别多的点,估计可能会超时,而且按照过题人数来看,不大可能是这样的做法,但是发现好多人都这么做而且过了,这个后面再说。
本文的做法就是利用纯数学的方法来找圆和圆的公切线带来的切点坐标,拿这些坐标来构造凸包,具体细节我们在下文讨论。
我见到的一些别人的做法
就像我队友预见的那样,如果我在每个圆上取得的点足够多,这些点就组成了一个圆,拿这些点来算凸包周长,理论上是可以算出一个近似的结果。事实上也确实如此,在每个圆上取5000个点然后正常凸包计算是可以把这个题给卡过去的。如果让我优化的话,我可能会让小一点的圆上取的点少一点,大的圆上的点取得多一点,这样保证精度的同时似乎能让速度快一点。我很赞同这样的做法,在比赛中充分利用人类智慧用更短的时间拿到更多的分数是很重要的。
我的具体做法
首先使用纯数学的方法求出每个圆直接公切线和圆相切的切点坐标,复杂度是\(O(n^2)\)。因为显然的最后在凸包上的圆的点都是切点,而构成凸包的线是切线和圆的弧。接下来拿这些切点去构造凸包。最后计算周长的时候,如果凸包上的两个点在同一圆上则计算弧长,否则计算欧几里得距离。最后相加即可。
但是要注意的是我这么写第一次错了,下面这个样例可以轻松卡掉这个做法,这也是所以使用公切线做法的人需要注意的。
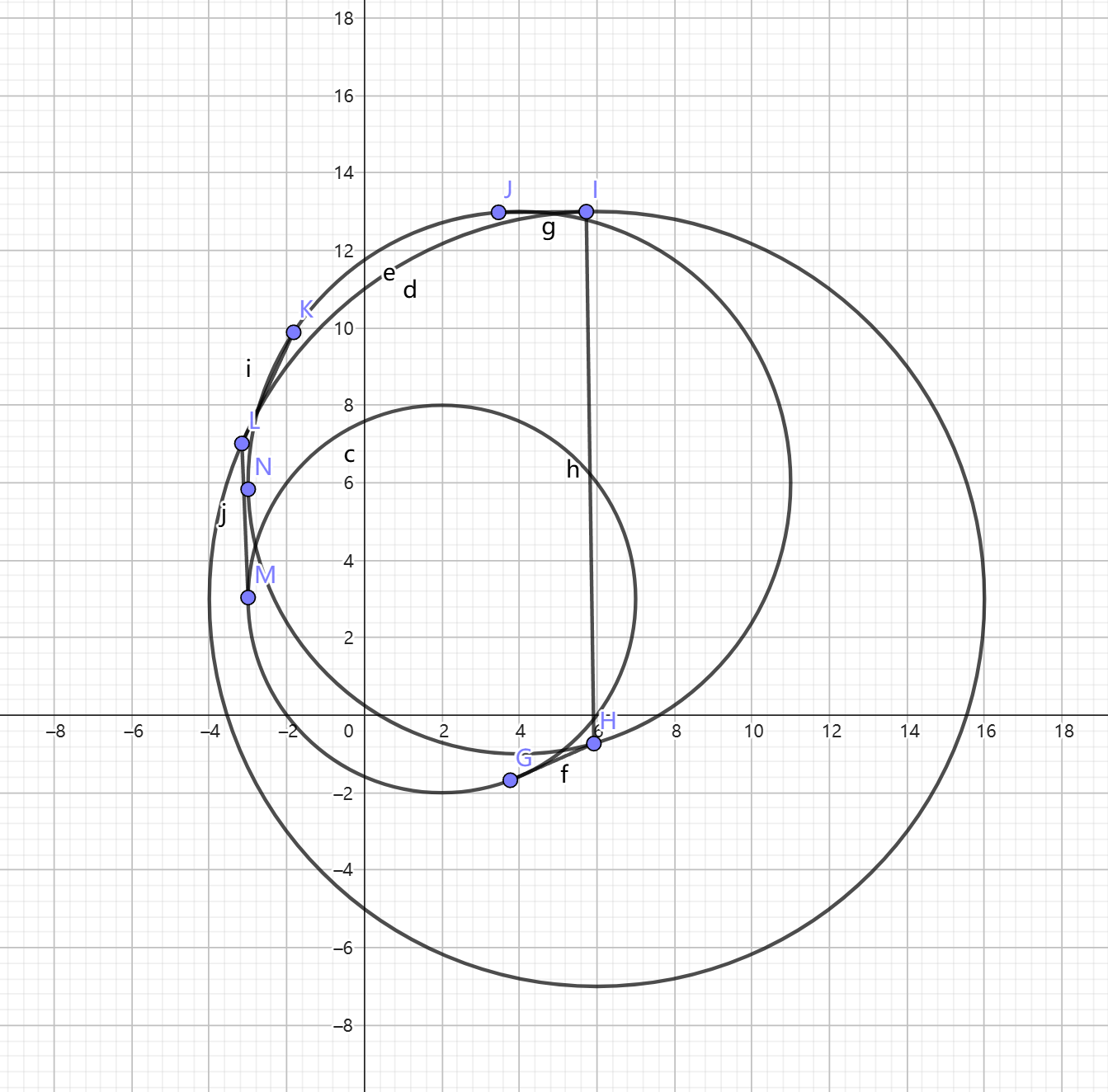
如图所示,我们构造出了所有的切点,但是在切点构造凸包的时候,我们无法构造出正确的凸包,最下面和最右面的圆弧我们无法包括起来。我的队友天赋异禀、聪明过人提出了一个天才的想法:“会发生这样的主要原因显然是有的圆被直接包裹起来了,我们\(O(n^2)\)把被完全包裹的圆给删掉就好了”。显然他是正确的,我的队友对这个题连续两次都提出了天才般的想法但都没被我采纳。我的做法更为愚蠢一点:既然仅靠切点没法完全描述这个凸包,我在上面再加一些点来引导构造凸包怎么样呢。
显然的,最终凸包包含这些十分关键的切点,但这些切点并不是全部,还有一些圆弧上的点,我人为地加上一些圆弧上的点来辅助引导构造凸包便可以得到正确答案。
我很佩服我的队友,能想出这么多正确又快速的做法,他具有那种很罕见的人类智慧。也希望大家在比赛的时候能多听取队友的意见吧。
好的,做法讲完了,来看具体实现吧。
具体实现
找切点
第一种情况
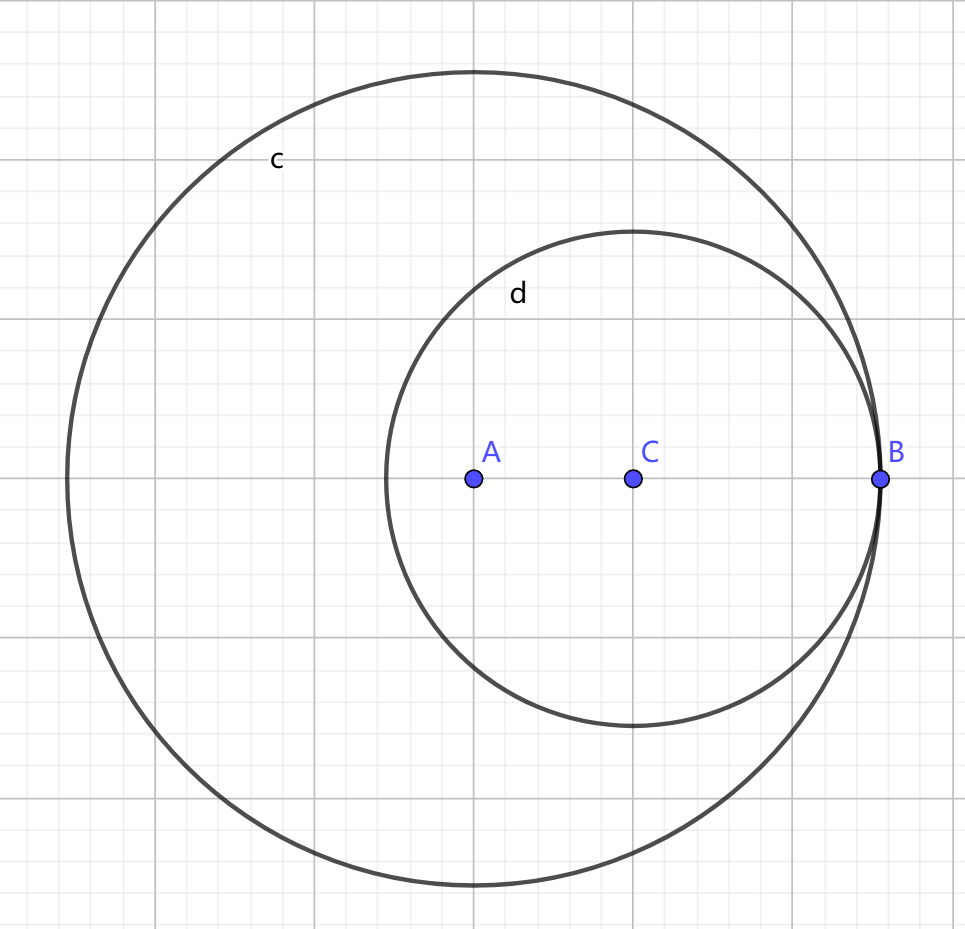
如果两个圆是包含关系,显然,它们没有切点。就像下面这样它们没有切点,我们直接跳过

代码描述为
if (tempdis + min(yuan[i].r, yuan[j].r) < max(yuan[i].r, yuan[j].r) || (yuan[i].x == yuan[j].x && yuan[i].y == yuan[j].y))
continue;
第二种情况
如果两个圆是相切关系,那么记录切点。如下图所示。
代码描述为
if (yuan[i].r > yuan[j].r)
{
if (abs(tempdis + yuan[j].r - yuan[i].r) < eps)
{
arr[++posi].x = yuan[i].x + yuan[i].r * cos(theta);
arr[posi].y = yuan[i].y + yuan[i].r * sin(theta);
arr[posi].id = i;
}
}
其中tempdis 为两圆圆心的距离,theta为两圆圆心的连线形成的直线和x轴形成的夹角。
第四种情况
两圆相离一些,当然我们不用像高中数学那样考虑四条公切线做出好多个切点,我们只要考虑最外面的切线和它们带来的切点就行,因为显然的只有这些点会出现在最后的凸包上。
如下图所示
4.1
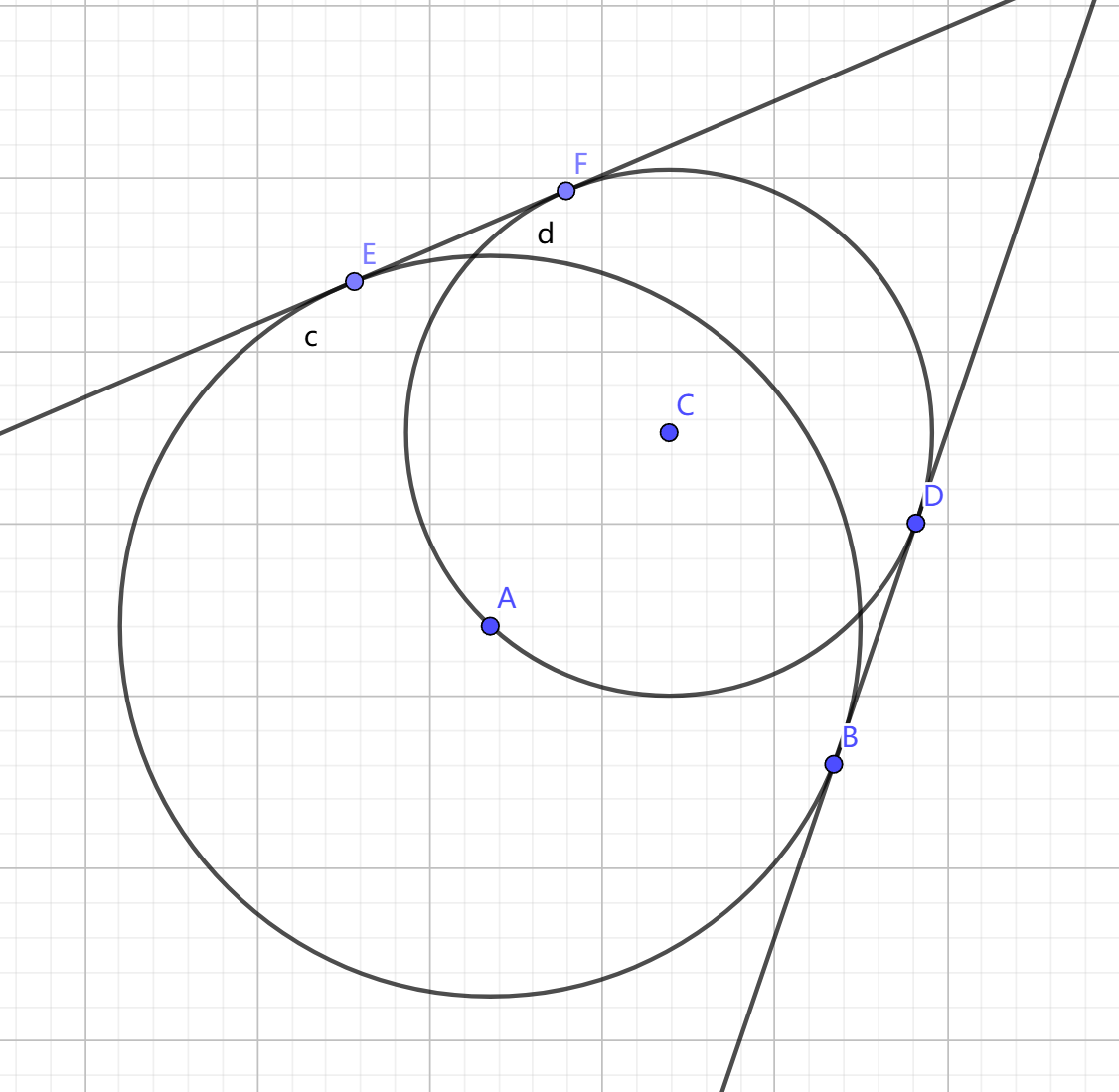
4.2
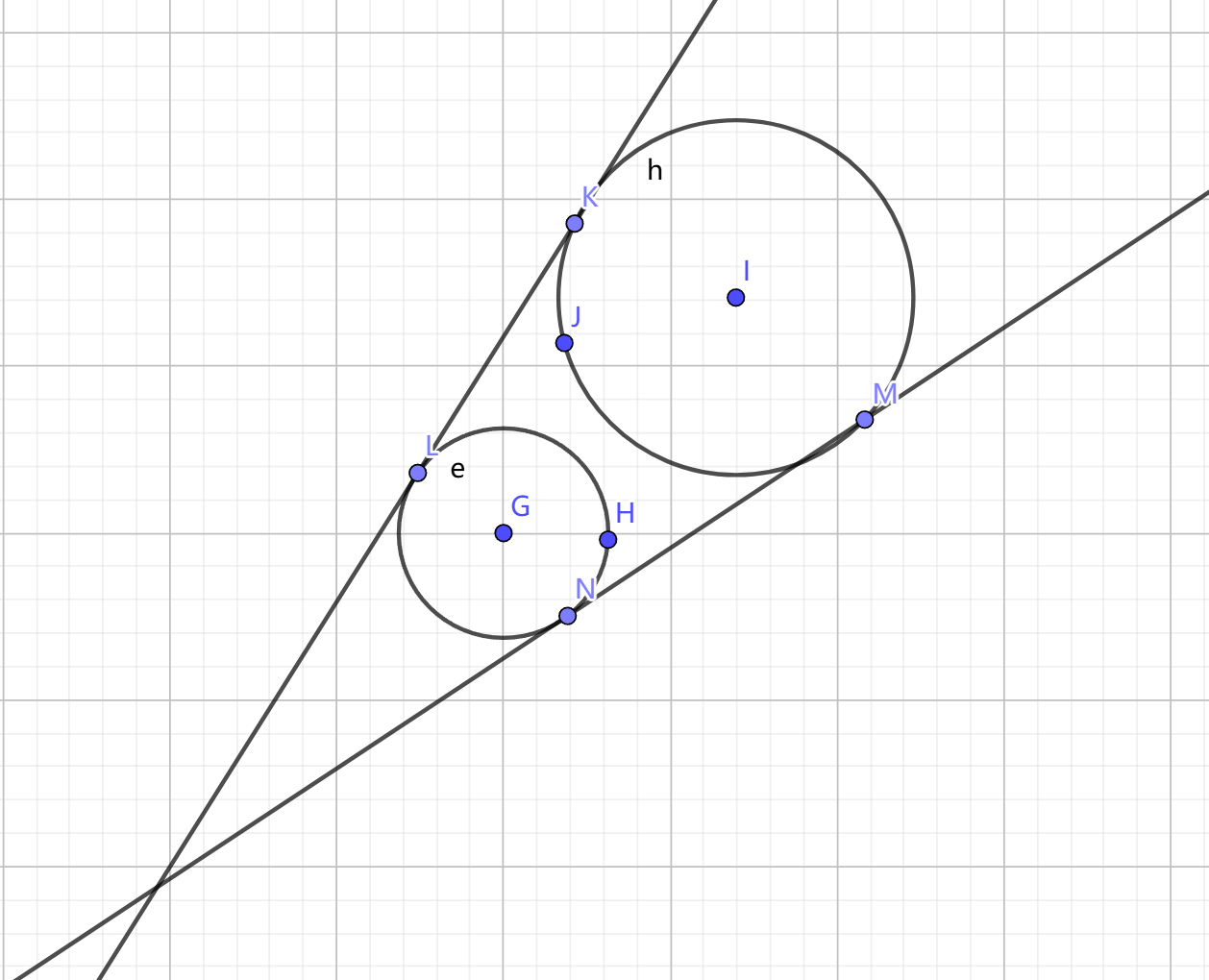
首先我们做出公切线和两圆圆心连线的交点,这个交点的坐标我们使用相似三角形也是可以算出来的。如下图所示
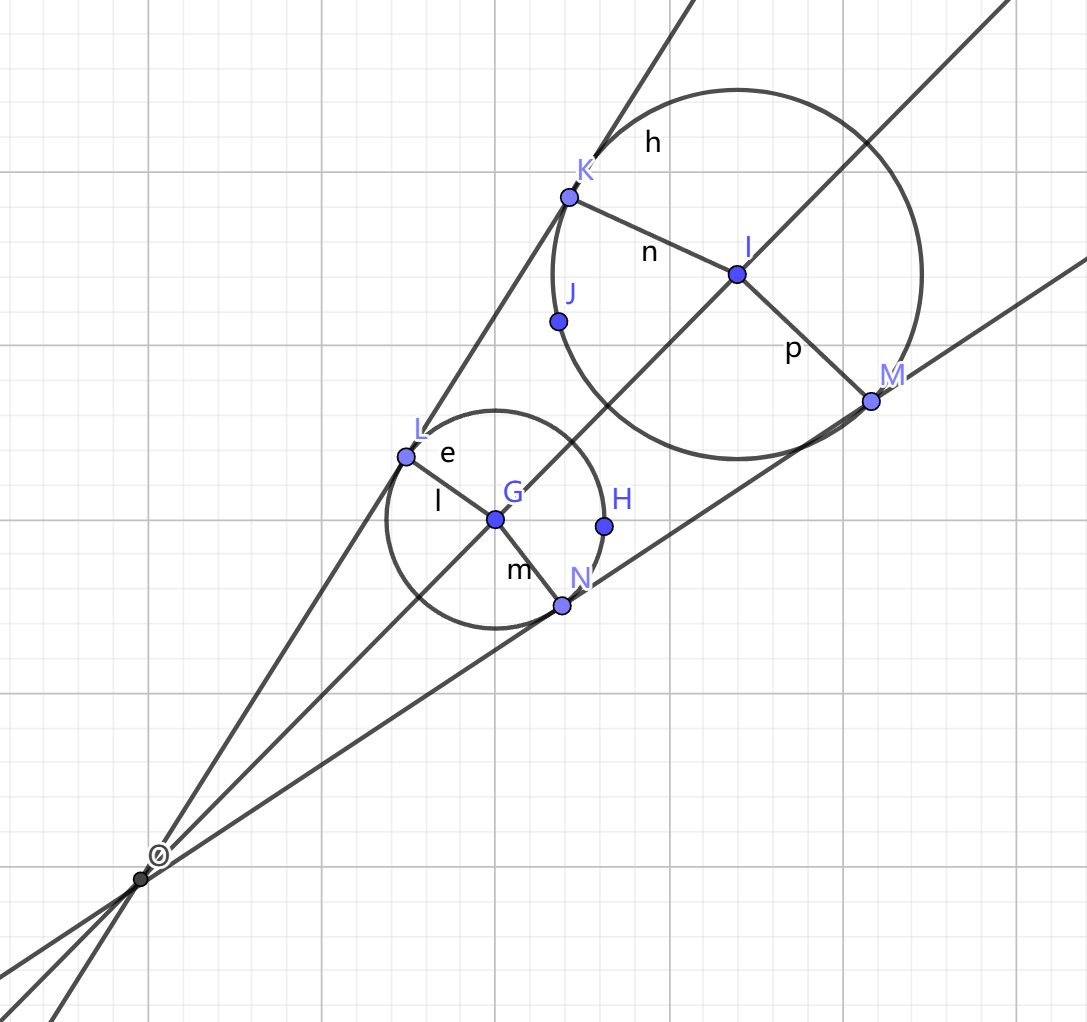
如图所示\(\triangle OLG\)和\(\triangle OIK\)是相似三角形,我们很容易计算出点\(O\)的坐标,有了点\(O\)的坐标的坐标之后,我们可以计算出\(\angle{\text{LOG}}\)的大小,于是我们就知道了直线\(OL\)和x轴的夹角,通过勾股定理计算出\(OL\)的长度,我们就得到了\(L\)的坐标,同理我们也可以得到\(N\)的坐标,于是所有的切点坐标我们就算出来了。
用代码表示为
p wai;
wai.x = (yuan[i].x) - tempdis / (yuan[j].r - yuan[i].r) * yuan[i].r * cos(theta);
wai.y = (yuan[i].y) - tempdis / (yuan[j].r - yuan[i].r) * yuan[i].r * sin(theta);
ld waiToYuan = dis(wai, yuan[i]);
ld thete2 = asin(yuan[i].r / waiToYuan);
ld zhijiaobian = sqrt(waiToYuan * waiToYuan - yuan[i].r * yuan[i].r);
theta = atan2(yuan[i].y - wai.y, yuan[i].x - wai.x);
arr[++posi].x = wai.x + zhijiaobian * cos(theta - thete2);
arr[posi].y = wai.y + zhijiaobian * sin(theta - thete2);
arr[posi].id = i;
arr[++posi].x = wai.x + zhijiaobian * cos(theta + thete2);
arr[posi].y = wai.y + zhijiaobian * sin(theta + thete2);
arr[posi].id = i;
值得注意的是,如果两圆的半径相同,我们无法通过上面的方法来求,不过也好说,拿角度关系和切线和半径垂直的关系很快就可以得到切点坐标
用代码表示为
if (abs(yuan[i].r - yuan[j].r) < eps)
{
arr[++posi].x = yuan[i].x + yuan[i].r * cos(theta + 3.14159265358979 / 2.0);
arr[posi].y = yuan[i].y + yuan[i].r * sin(theta + 3.14159265358979 / 2.0);
arr[posi].id = i;
arr[++posi].x = yuan[i].x + yuan[i].r * cos(theta - 3.14159265358979 / 2.0);
arr[posi].y = yuan[i].y + yuan[i].r * sin(theta - 3.14159265358979 / 2.0);
arr[posi].id = i;
continue;
}
加点
在刚刚的分析中我们提到,需要一些圆上的点来引导构造凸包,这里在每个圆上随便取一些就好,笔者选择了在每个圆上等距离取87个点,虽然也有每个圆上取5000个点的暴力算法之嫌,但是取87个点毕竟还是要快不少
用代码表示为
ld chafen = 3.14159265358979 * 2.0 / 87.0;
_rep(i, 1, n)
{
ld jiaodu = 0;
_rep(j, 1, 87.0)
{
arr[++posi].x = yuan[i].x + yuan[i].r * cos(jiaodu);
arr[posi].y = yuan[i].y + yuan[i].r * sin(jiaodu);
arr[posi].id = i;
jiaodu += chafen;
}
}
找凸包
很经典的算法了这里不再赘述,这部分不是很会的同学可以去洛谷找凸包的板子来做。
下面给出代码
int imin = 1;
ld ymin = 3e30;
ld xmin = 3e30;
_rep(i, 1, posi)
{
if ((arr[i].y < ymin && abs(arr[i].y - ymin) > eps) || (abs(arr[i].y - ymin) < eps && (arr[i].x < xmin) && abs(arr[i].x - xmin) > eps))
{
ymin = arr[i].y;
xmin = arr[i].x;
imin = i;
}
// cout << fixed << setprecision(20) << i << "min " << xmin << " " << ymin << endl;
}
point temppp;
temppp = arr[1];
arr[1] = arr[imin];
arr[imin] = temppp;
sort(arr + 2, arr + 1 + posi, cmp);
int pp = 1;
for (int i = 2; i <= posi; i++)
{
if (abs(arr[i].x - arr[i - 1].x) > eps || abs(arr[i].y - arr[i - 1].y) > eps)
arr[++pp] = arr[i];
}
posi = pp;
int cnt = 0;
st[++cnt] = arr[1];
for (int i = 2; i <= posi; i++)
{
while (cnt > 1 && crossMull(st[cnt - 1], st[cnt], st[cnt - 1], arr[i]) <= 0)
cnt--;
st[++cnt] = arr[i];
}
st[cnt + 1] = arr[1];
计算
就像我之前说的那样,如果凸包上的两个点在同一个圆上,那么我计算两点的弧长,由于凸包上的点是有一定的顺序的,计算弧长的时候注意一下是逆时针还是顺时针就行了;对于不在同一个圆上的点,那就更简单了,直接计算两点间的的欧几里得距离就行。
用代码描述为
_rep(i, 1, cnt)
{
// cout << st[i].x << ' ' << st[i].y << ' ' << st[i].id << ' ';
if (st[i].id == st[i + 1].id)
{
ld the1 = atan2(st[i].y - yuan[st[i].id].y, st[i].x - yuan[st[i].id].x);
ld the2 = atan2(st[i + 1].y - yuan[st[i].id].y, st[i + 1].x - yuan[st[i].id].x);
if (the1 < 0)
the1 += 3.14159265358979324 * 2.0;
if (the2 < 0)
the2 += 3.14159265358979324 * 2.0;
if (the2 <= the1 + eps)
the2 += 3.14159265358979324 * 2.0;
sum += (the2 - the1) * yuan[st[i].id].r;
}
else
{
sum += dis(st[i], st[i + 1]);
}
}
最后华丽地输出答案就行了。
完整代码
由于计算几何中涉及很多乱七八糟的函数,而且其中有一些细节上文似乎也没有交代明白,这里为了更方便大家理解,附上我的源代码,码风较丑。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
#define endl '\n'
#define _rep(i, a, b) for (int i = (a); i <= (b); ++i)
#define rep(i, a, b) for (int i = (a); i < (b); ++i)
#define Forget_that return
#define Just_go 0
#define Endl endl
#define ednl endl
#define eldn endl
#define dnel endl
#define enndl endl
#define Ednl endl
#define Edml endl
#define llmax 9223372036854775807
#define intmax 2147483647
ld eps = 1e-9;
struct point
{
ld x;
ld y;
int id;
} arr[1000006], st[1000006];
struct p
{
ld x;
ld y;
ld r;
} yuan[10000];
ld crossMull(const point &a1, const point &a2, const point &b1, const point &b2)
{
return (a2.x - a1.x) * (b2.y - b1.y) - (b2.x - b1.x) * (a2.y - a1.y);
}
ld dis(const point &a, const point &b)
{
return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
ld dis(const p &a, const p &b)
{
return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
ld cmp(const point &a, const point &b)
{
ld temp = crossMull(arr[1], a, arr[1], b);
if (temp > 0)
return true;
if (temp == 0 && dis(arr[1], a) < dis(arr[1], b))
return true;
return false;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;
cin >> n;
_rep(i, 1, n)
{
cin >> yuan[i].x >> yuan[i].y >> yuan[i].r;
yuan[i].r += 10;
}
int posi = 0;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
if (i == j)
continue;
ld tempdis = dis(yuan[i], yuan[j]);
ld theta = atan2(yuan[j].y - yuan[i].y, yuan[j].x - yuan[i].x);
if (tempdis + min(yuan[i].r, yuan[j].r) < max(yuan[i].r, yuan[j].r) || (yuan[i].x == yuan[j].x && yuan[i].y == yuan[j].y))
continue;
if (yuan[i].r > yuan[j].r)
{
if (abs(tempdis + yuan[j].r - yuan[i].r) < eps)
{
arr[++posi].x = yuan[i].x + yuan[i].r * cos(theta);
arr[posi].y = yuan[i].y + yuan[i].r * sin(theta);
arr[posi].id = i;
}
}
if (abs(yuan[i].r - yuan[j].r) < eps)
{
arr[++posi].x = yuan[i].x + yuan[i].r * cos(theta + 3.14159265358979 / 2.0);
arr[posi].y = yuan[i].y + yuan[i].r * sin(theta + 3.14159265358979 / 2.0);
arr[posi].id = i;
arr[++posi].x = yuan[i].x + yuan[i].r * cos(theta - 3.14159265358979 / 2.0);
arr[posi].y = yuan[i].y + yuan[i].r * sin(theta - 3.14159265358979 / 2.0);
arr[posi].id = i;
continue;
}
p wai;
wai.x = (yuan[i].x) - tempdis / (yuan[j].r - yuan[i].r) * yuan[i].r * cos(theta);
wai.y = (yuan[i].y) - tempdis / (yuan[j].r - yuan[i].r) * yuan[i].r * sin(theta);
ld waiToYuan = dis(wai, yuan[i]);
ld thete2 = asin(yuan[i].r / waiToYuan);
ld zhijiaobian = sqrt(waiToYuan * waiToYuan - yuan[i].r * yuan[i].r);
theta = atan2(yuan[i].y - wai.y, yuan[i].x - wai.x);
arr[++posi].x = wai.x + zhijiaobian * cos(theta - thete2);
arr[posi].y = wai.y + zhijiaobian * sin(theta - thete2);
arr[posi].id = i;
arr[++posi].x = wai.x + zhijiaobian * cos(theta + thete2);
arr[posi].y = wai.y + zhijiaobian * sin(theta + thete2);
arr[posi].id = i;
}
}
ld chafen = 3.14159265358979 * 2.0 / 87.0;
_rep(i, 1, n)
{
ld jiaodu = 0;
_rep(j, 1, 87.0)
{
arr[++posi].x = yuan[i].x + yuan[i].r * cos(jiaodu);
arr[posi].y = yuan[i].y + yuan[i].r * sin(jiaodu);
arr[posi].id = i;
jiaodu += chafen;
}
}
int imin = 1;
ld ymin = 3e30;
ld xmin = 3e30;
_rep(i, 1, posi)
{
if ((arr[i].y < ymin && abs(arr[i].y - ymin) > eps) || (abs(arr[i].y - ymin) < eps && (arr[i].x < xmin) && abs(arr[i].x - xmin) > eps))
{
ymin = arr[i].y;
xmin = arr[i].x;
imin = i;
}
// cout << fixed << setprecision(20) << i << "min " << xmin << " " << ymin << endl;
}
point temppp;
temppp = arr[1];
arr[1] = arr[imin];
arr[imin] = temppp;
sort(arr + 2, arr + 1 + posi, cmp);
int pp = 1;
for (int i = 2; i <= posi; i++)
{
if (abs(arr[i].x - arr[i - 1].x) > eps || abs(arr[i].y - arr[i - 1].y) > eps)
arr[++pp] = arr[i];
}
posi = pp;
int cnt = 0;
st[++cnt] = arr[1];
for (int i = 2; i <= posi; i++)
{
while (cnt > 1 && crossMull(st[cnt - 1], st[cnt], st[cnt - 1], arr[i]) <= 0)
cnt--;
st[++cnt] = arr[i];
}
st[cnt + 1] = arr[1];
ld sum = 0;
_rep(i, 1, cnt)
{
// cout << st[i].x << ' ' << st[i].y << ' ' << st[i].id << ' ';
if (st[i].id == st[i + 1].id)
{
ld the1 = atan2(st[i].y - yuan[st[i].id].y, st[i].x - yuan[st[i].id].x);
ld the2 = atan2(st[i + 1].y - yuan[st[i].id].y, st[i + 1].x - yuan[st[i].id].x);
if (the1 < 0)
the1 += 3.14159265358979324 * 2.0;
if (the2 < 0)
the2 += 3.14159265358979324 * 2.0;
if (the2 <= the1 + eps)
the2 += 3.14159265358979324 * 2.0;
sum += (the2 - the1) * yuan[st[i].id].r;
}
else
{
sum += dis(st[i], st[i + 1]);
}
}
ld maxR = -10;
for (int i = 1; i <= n; i++)
{
maxR = max(maxR, yuan[i].r);
}
cout << fixed << setprecision(10) << max(maxR * 2.0 * 3.14159265358979324, sum) << endl;
Forget_that Just_go;
}
总结
我觉得这道题不是很精妙,但对于训练计算几何还是挺有帮助的。写这么长的代码确实很能锻炼我们的代码力,当然如果我当时听从队友的方法,这道题说不定很快就可以做完。
按照我的做法能在109毫秒跑完,比每个圆上暴力加点的做法要快不少,但是我相信我的做法十分不完善,加点的做法以及取弧长的做法,以及计算切点的方法都让感觉不是很到位,让我觉得我一定可以被一组样例给hack掉,这篇题解可能更多地是提供一种不同于暴力加点做法的思路吧,希望对大家有帮助。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号