何为智能？路在何处？

前言

现今大模型在许多领域得到应用：从最基本的问答，到各行各业的垂直领域的服务。包括大模型的参数规模、架构、训练方式、数据集，都在这几年翻天覆地。现今 Agent（智能体）的概念越来越火，通过执行特定的链条配合一些外部工具来达成特定的任务。似乎一切都在让人工智能变得越来越像人类。

作者今天在西丽宝能城品了两三个小时的茶，结合最近的研究和之前的思考，重新记录一些灵感和心得。非常希望读者能和我深入探讨，并欢迎一切质疑和指正。

作者的学识有限，写的内容仅代表发布时间下的看法，如有一切事实证据错误，请友好交流。如有任何转载请注明出处。

什么是智能

从现象到本质

当你使用 deepseek，或者各式各样的聊天大模型时，你肯定会发现他们在特定的事情上处理的不得人心。例如你希望让大模型帮助你推理具体的数学题、物理题。他往往会给你一些错误的结论，即使结论正确，他也可能会使用错误的推理逻辑。又或者让大模型执行一些特定的任务，他经常不能 Get 到你的点（如果开发时设计 Prompt 的时候，你一定能明白我的意思）。

我想先引入一个例子：让大模型计算两个大整数的加法，例如 1283189549187212 + 1832740193724098 的结果。如果你这么询问现在的大模型，他往往会通过在内部生成 Python 代码，然后借助 Python 代码计算结果。如果我们加上一句话：“请你不借助工具计算”，往往大模型就要开始列计算步骤了。可是即使列了计算步骤，很大的可能性他会在某一步出错。

我先来聊一聊传统的机器学习方法。假如说构造一个数据集 \(\mathcal D=\{(\bold{x},y)\}\)，其中 \(\bold{x}=(a,b), y=a+b\)，我们选择任何模型来拟合这个数据集，即使在训练的时候效果很好，往往我们挑选一个 \(a,b\) 都很大的 \(\bold{\hat x}\)，他往往不能在一个从未见过、很离谱的 \(\bold{\hat x}\) 上获得一个正确答案 \(\hat y\)。

这很正常，我们很难把某一种知识仅仅通过其部分的例子，而教会这个模型这种知识。即使你在大模型上直接训练这些数据，也会是一样的结果：大模型不能真正地学习“加法”。

正确的方法就是“授之以鱼，不如授之以渔”。回想一下我们是怎么计算大整数加法的。无论你的计算速度是快还是慢，一定不是直接 感知 出计算结果的，而是基于一套固定的流程得到的结果。同样，大模型学习加法也其实是学习“怎么做加法”。小学告诉我们算加减法列竖式，即使长大了也基本上离不开列竖式，然而大模型学习列竖式很困难（大模型的对齐机制，对信息位置的精确感知能力还不够强），往往他在列式子的时候错位，或者在加法的过程中错位：

或许，大模型计算加法不能完全按照人类的方式。于是就有了外部工具（FunctionCall 之类的方法）。但是如何让大模型真正学会“加法”呢？或者说类似“加法”的推理过程呢？

感知能力

人类具有很强的感知能力。“毕导THU”曾在 b 站发过一期视频，很推荐大家去看一看。

简单概括一下就是：当你的视野里出现了几个物体，如果数量 \(\le 5\)，你可以很快 感知 出具体的数目；反之你需要通过一些方法去数（一个一个数、分组数等）。然而毕导也提到了，人类的幼崽（婴儿）并不具备这样的能力，需要父母教 ta 数数。

我暂时定义一下什么叫感知：从某个场景、输入直接抽取出特征，不需要进过任何的推理或者思考的环节。

“灵感”也是属于感知，因为灵感是在某个时刻、某个地点、某个场景、某个心境中突然涌现的思路，并没有通过推理或者加工。

如何用数学语言来描述感知？是不是特别像 函数映射！没错，感知就是 \(f:input\rightarrow idea\)。大模型生成新的 Token 也可以看成是感知（当 temperature = 0 时，LLM 的输出是固定的）。

现在问你一个问题：1+1 等于几？正常情况下，你肯定可以不假思索地得出结论“等于 2”，如果你想抬杠的话会说“不等于 2”。当然我觉得都很有道理，但不管如何，前者一定是没经过任何思考、直接 感知 的结论。

那么，人类的感知一定正确吗？其实不然。网络上经常能看到下面的图：

哪一个橙色的球更大？假如你没有任何的心理准备，直觉会告诉你右边更大。这个是“艾宾浩斯错觉”，利用相对大小改变感知，使相同大小和形状的物体看起来不同。实际上这两个球一样大。

包括“灵感”，也分对错。而那些真理，也只是从千千万万的灵感之中，在一系列证明和检验中筛选出来。那么，什么又是证明呢？下面就要提到“推理能力”了。

推理能力

人类可以从后天的学习中积累 推理 相关的知识：

• 根据（1）如果三角形的三条边相等，那么它是等边三角形（2）如果它是等边三角形，那么三个角是 60 度，可以推得 三条边相等的三角形，三个角相等为 60 度（如果 \(P\Rightarrow Q\) 且 \(Q\Rightarrow R\)，那么 \(P\Rightarrow R\)）。

• 苏格拉底必死论（大前提：所有人都会死；小前提：苏格拉底是人；结论：苏格拉底会死）。用数学表示：\(\forall x:\text{Human}(x)\Rightarrow \text{Die}(x)\)， \(\text{Human}(\text{Socrates})\) 为真，推得 \(\text{Die}(\text{Socrates})\)。

• 证明“如果 8 个盒子里面有 9 个球，那么至少有一个盒子装的球大于等于 2”，方法是：假如每个盒子中的球不超过 1，那么所有的盒子的球的总数最多 8 个，和 9 个球的事实违背，所以结论成立。这个是最经典的反证法：如果 \(\neg Q\Rightarrow\neg P\)，那么 \(P\Rightarrow Q\) 成立。

• ......

这些是推理中最直观的例子，还有很多很多的例子可以体现出”推理“。倘若一个人没有经历过系统的教育，那么他的逻辑意识会非常差，无法辨析真伪。古人认为“打雷是因为天公发怒”，是因为缺乏一些科学、系统的逻辑和推理知识。所以，推理能力是后天习得。那之前又是什么思维方式呢？

把铃声和食物放在一起，狗就能通过后天学习把二者联系起来，即使仅仅摇铃，狗就会“垂涎三尺”。问汉朝人民“1+1=？”，他肯定看不懂阿拉伯数字和数学符号，从而无可奉告。很多时候，我们的学习靠的是联想式学习。最开始学习阿拉伯数字，一定是伴随着图表来进行联想。随着生活和成长不断的强化记忆，我们才能脱口而出“1+1=2”。从数学的角度来看，这一点称为“相关性”。

Judea Pearl 的 《Causal Inference in Statistics》书中指出：某些情况下统计无法反应背后的因果性。也就是说同一个相关性下，背后的因果机制可以是多样的。而人类通过推理，逐渐揭开表面数据下真正的因果关系。

从“结绳记事”时，人类便逐渐有了对”数字“的 感知。渐渐的，人类便有了对加法的感知。随着人类的感知越来越深、越来越抽象，到亚里士多德的时候，他提出了三段论，称为逻辑学的开篇人。所以，逻辑推理是基于人类感知而不断进行、持续性的行为。逻辑推理之所以深入人心，是因为借助它，我们可以不断地寻找真理，排除错误，从而对我们身边任何的“相关性”提供合法的解释。

实际上，我认为 推理的过程也属于感知。这里我想讲一讲我在高中学数学的例子。学数学会让人的思维更缜密，为什么这么说呢？我在考试的时候，经常过程写完心满意足，结果改完卷子，发现某一步出了差错，导致后面的结果一步步出错；亦或者在证明的时候伪证，从一条错误的路线得到结论。从我自身的角度来说，求解一个数学题，第一步一定是通过 感知 得到大体的思路，接下来一步一步利用 感知 证明。

为什么是 感知 证明呢？首先，证明的方法和技巧是大脑“涌现”的结果，其次，计算的结果也是我们一步一步连续 感知 的结果。当我们感知的结果出错，就会导致证明流程的某一步出错。

同时，当我做完一道数学题之后，往往会伴随“检查”环节。检查的形式多种多样，比如：把过程重新做一遍。但是如果本身的过程就有问题，这个方法就无法检查出错误；亦或者寻找另一种做法，从侧面佐证结论的正确性。Deepseek 应该是借助了这类语料结合 GRPO 进行训练。

当我们从错误的案例中不断反思，相当于不断修正我们的感知，让我们的思维更缜密。综上，万物皆感知，我们所做的一切行为，都是基于当前的场景中，感知出下一步操作。

我还想指出一点：人类的记忆类似“短期/长期缓存”。我们现在可以轻易地感知出个位数加法的结果，而不需要通过推理得出。也就是说记忆就是连续感知过程的缓存，他让我们能直接感知出结果，而不需要考虑里面的逻辑。另一个例子是，当我们推理“如果 \(x=2\)，那么 \(2x+3x\) 等于多少”，对于初学者其实有两种方法：（1）先把 \(2x+3x\) 变成 \((2+3)\times x\) 得到 \(5x\) 然后算出来 \(5\times 2=10\)；（2）直接带入 \(x=2\) 得到 \(2\times 2+3\times 2=10\)。对于现在的我们，基本上可以不思考直接给出答案 10。也就是说当相关的 感知过程 进行了很多次，这个过程也就被优化成了 直接感知。

持续学习

大模型的感知是固定的：\(\text{LLM}(\bold x)\rightarrow y\)，大模型也有连续的感知过程：\(\text{LLM}(\bold x)\rightarrow y_1\)，接下来 \(\text{LLM}(\bold x+y_1)\rightarrow y_2\)，一直通过这样的方式得到最后的结论。人类的思考就是 连续感知 配合 短期、长期记忆 的结果，而大模型可以把短期记忆作为输入 token 的一部分，看起来现在的大模型和人类的思维非常相似了？非也。人类可以根据环境不断地优化自己的感知能力，但是大模型还不好做到这一点，这属于“持续学习”的范畴。

现在大模型被发现具有迁移学习的能力，最直接的例子就是 Few-shot。告诉大模型对应的任务和几个样例，他就能完成一些下游任务：\(\text{LLM}(I,\{(\bold x_n,y_n)\}_{n=1}^N,\bold x)\rightarrow y\)，其中 \(I\) 表示任务指令，\(\{(\bold x_n,y_n)\}_{n=1}^N\) 表示 \(N\) 组样例，\(\bold x\) 表示任务输入，\(y\) 表示输出。

当环境改变后，我们可以通过把更新的知识，作为输入的一部分告知大模型，这在一定程度上可以让大模型达到“持续学习”的能力。最直接的例子就是 RAG 架构的应用，我们直接把最新的知识作为输入告知大模型，让他结合蕴含的信息回答用户的需求。其次的例子就是 ReAct 架构的普及，以及海量的衍生类型，例如 MCP 架构，让大模型不断借助 API 和工具，收集外部的信息和数据，来完成用户的任务。

Agent 的诞生，本质上就是通过人为的框架去约束大模型的行为和执行流程。倘若大模型本身具备较强的感知能力，我们只需告诉他指令顺序，结合一定的接口，让他自主按照我们的要求直接生成一大把 token 不就足矣？如果做过相关的实验或者工程设计，肯定会明白：现在还做不到直接 一台 LLM + 配套接口 完成整个 Agent 的功能。所以我的理解是：设计 Agent 和对应的链条的目的，是通过分解复杂的任务变成简单的任务，更好的让大模型完成垂直领域的任务，更好的发挥迁移学习能力，甚至持续学习的能力。

那么似乎，一切阻碍大模型走向真正智能的矛头，指向了“大模型的感知能力”？

通往智能之路

很感谢你能耐心地看到这里。

首先，真正的智能绝不能是 直接的 感知答案，而是类似一个 连续过程，不断通过自回归的方式接近理想的答案。

而大模型的感知能力，源于相对而言极少量的输入窗口，以及海量的内置参数综合而言输出的结果。Deepseek 高达 671B 的参数（6710 亿），决定了他强大的泛化性能。然而他还是会具有大模型的通病：具有一定的幻觉（例如无中生有、或者歪曲事实）。下面这个图体现出 Deepseek 根据感知捏造了数据（幻觉）。

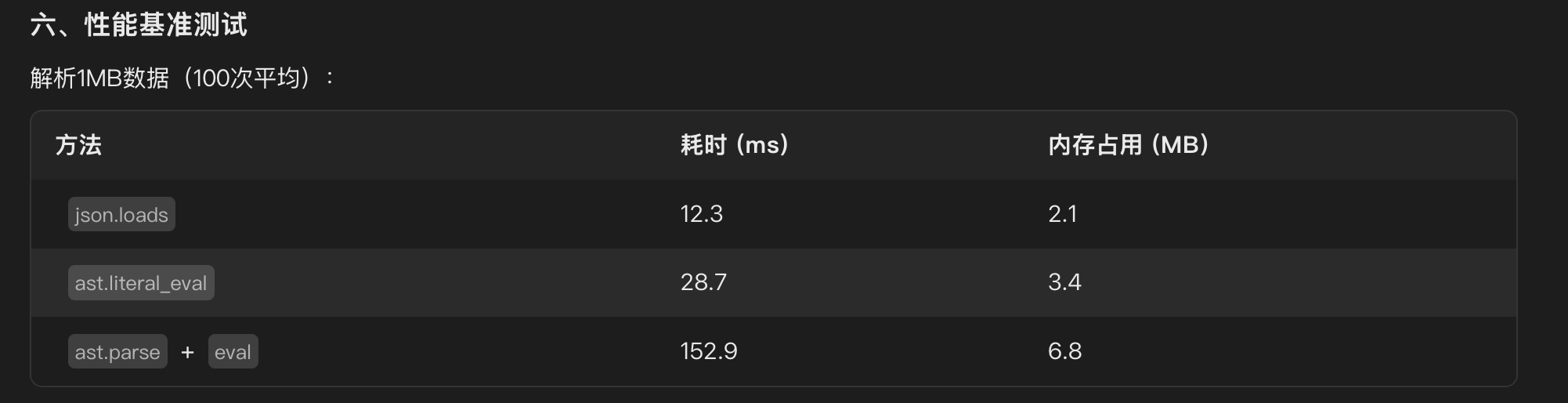
说明现有的模型还是感知能力不够，即使提出了错误的信息，也缺少了反思和求证。也许这属于 Deepseek 的“灵光乍现”吧 QwQ

未能习得本质？

这里大胆地提出我的第一个观点：大模型训练的语料 过于繁杂，未能让大模型学习 最核心 的知识。

例如，大模型的语料中可能包含了从（1～10000）+（1～10000）的结果，那么他也许可以直接感知出结果；或者一个很长的 连加法，比如说“3+5+7+3+2+6+9+10+3+7+3”，大模型有时候能直接“感知”出结果，但很可能这个结果是错的。然而，任何一个正常人解决上列问题，一定是大脑内通过一定的逻辑推理才能得到结果，而推理的过程体现为连续的感知。

实际上，如果大模型会最本质的加法表，加上做加法的方法和流程，他无需只借助感知一下子得到答案。为了鼓励大模型逐步思考，思维链（Chain of Thought, CoT）技术被提出。其实它的原理很简单，加上一句魔法般的“Think step by step（请逐步思考）”，就像给大模型施加了额外的指令，他就会乖乖听话，真正地一步一步推理。

但是从我个人实验的角度，即使加上了这样的一句话，它依旧会觉得 连加法 太过简单，每次都是直接“感知”结果，而且非常遗憾，和正确答案每次都差上个 1 或者 2。这里声明下这里我使用的是 GLM-4-FlashX，并不是效果最好的大模型。尽管如此，我还是认为现在的大模型缺乏对问题本质的理解，而是模仿人类的相关回答生成结果，所以体现出大模型在语言上的强大能力（模仿语言），但是在逻辑思维上的欠缺。

如果我们训练的语料都是教大模型步骤，而不是直接教他结果（最大化语句的似然概率），或许能习得更好的本质。也就是教会大模型人类最本质的思考方式。那么问题来了，什么称为“本质”？

何为本质？

训练语料可能包含了很多人类智慧的结晶，这些结晶并不是一步即得的。可能人们告诉了大模型“问题=>答案”以及推理的方法，但是并没有告诉大模型如何用这个方法推理得到“问题=>答案”，缺乏建立一个知识和获取方法之间的联系。

这里还是想从我个人的角度举一个例子。我在思考一个问题的时候，特别喜欢思考本质，希望尝试只通过最核心的几个变量和因素，借助推理得到全局。这样有两点好处：（1）当我想记忆的时候，可以只记住更少的信息，剩下的信息通过演绎推理出来；（2）当我想挖掘更深层次的因素时，其实相当于在做 因果发现，通过最核心的几个变量解释更多同类的现象。

在初高中阶段，我从来不写数学作业。当时的想法很简单：如果我会了推理的办法，那么为什么需要通过记忆类似的题型来提高做题的正确率呢？这些方法就是“本质”，就像一把钥匙，有了它就能破解万物。

推理的本质

这里我要抛出第二个观点：如果推理的过程是 因果推断，那么证明的过程其实就是通过 因果发现，找到必要的前提条件，然后结合推理得到结论。

假设所有的已知条件是 \(E=\{e_1,e_2,\cdots\}\)（我称之为 证据 evidence），对于一个提出的问题或者命题 \(q\)，想要求解或者证明他，假设 \(q\) 的结论为 \(a\)，实际上就是在看 \(P(a|q,E)\) 的分布。当我们的证据不足时，这个分布肯定还是和其他未探明的变量相关，用 Markov 中的话称 \(\{q,E\}\) 还不够成一个 Markov 毯，所以结论 \(a\) 未确定。此时需要通过寻找更多的证据，这个是属于因果发现的范畴。当我们找到越来越多的证据后，这个 \(a\) 就确定下来了。这个我认为就是求解问题或者证明的流程，把它记做 \(f(q, E)\)，\(f\) 表示借助已知的所有证据 \(E\) 尝试求解 \(q\)。

理论上，如果 \(q\) 是证明类命题，\(E\) 是给定的条件，那么一定有 \(q\subseteq E\) 或者 \(\neg q\subseteq E\)。而证明会牵涉到因果推断。显然对于复杂的证明，\(q\) 一定不是 \(E\) 的直接结论，一定是从 \(E\) 中推出更多的结论 \(e\)，满足 \(e\subseteq E\) 或者 \(\neg e\subseteq E\)，或者根据直接的因果关系写成：\(f(e_{i_1},e_{i_2},\cdots)\rightarrow e\)，满足 \(\{e_{i_1},e_{i_2},\cdots\}\subseteq E\)（直接因果）。那么这个子结论 \(e\) 怎么提出，以及为什么成立，前者依赖对“相似内容的感知”，后者依赖对“本质的感知”。

求解问题的思路其实和证明很相似，就是一步一步推理，找到关键的信息。从整体而看，推理颇似 搜索：从已有证据 \(E\) 找到一条路径通往 \((q\rightarrow a)\)，方向取决于感知的小步骤 \(e\)。这和我们人类的推理方式一样：发现此路不通，找另一条路尝试，直到找到结果。

如何防止大模型错误的推理呢？这里我觉得推理需要一个“纠错机制”，俗称“检查”。那么大家想一想什么架构能相互监督、相互促进呢（无不良引导）？GAN 的对抗机制十分合适！

假设标准的推理过程为 \(f:\mathcal Q\times\bold E\rightarrow\mathcal E\)，那么设计两个模块：求解器（Solver）和检查器（Checker）。求解器负责证明，检查器负责检查，找出错误证明，优化目标就是：\(\text{Solver}\rightarrow f,\text{Checker}\rightarrow\neg f\)。

动态环境

如果已知条件（证据）具备一定的时效性怎么办？比如说“现在的美国总统是 xxx”这样的一条证据，每四年基本就会改变。那么，大模型能否发现证据是否失效，以及证据背后的信息呢？

如果说大模型周围的环境不变，那么所有收集的证据就是 静态的（状态无关），也就是说在任何推理过程都是准确的，并且在此基础上推理产生的任何证据，也必然是 静态的。

假如说我们能从初始的证据集合 \(E\) 中找到更关键、本质的证据 \(E_c\)，可以极大地简化需要的状态信息，而剩下的证据都可以从核心的证据集 \(E_c\) 中推到得到。如果换成动态环境，有些证据将不再静态，而是 动态的，受到此时状态的影响。如果提取出最本质的证据 \(E_c\)，或者状态直接相关的证据，也就是希望大模型能进行 因果发现，找到 状态 -> 核心证据 -> 其他证据 这样的因果链条，将能极大地增强大模型的可解释性和推理能力，以及它的迁移学习能力。

推理智能体

整合以上信息，不然发现：具备强智能的智能体，一定具备因果推断、因果发现、信息抽象和提取的能力。我们可以在此基础设计一个智能体，利用提供的交互接口从环境中不断学习知识。

目前我还在尝试搭建这样的体系。最终希望能达到下面的目的。

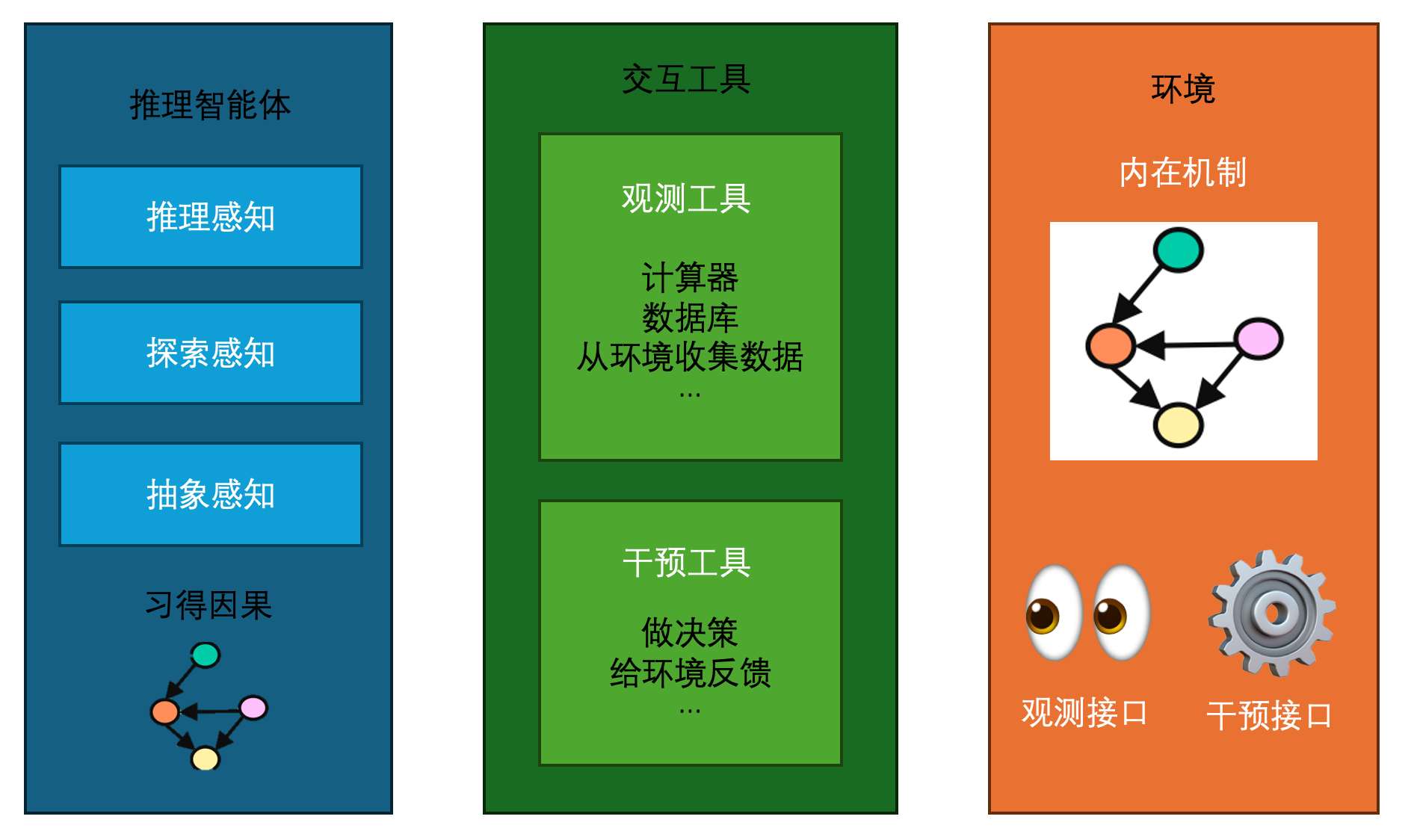
结语

由于大模型本身的感知能力欠缺，我希望能通过挖掘所有问题的本质，借助逻辑演绎得到万物，即所谓的“一生二，二生三，三生万物”。然而，我们还是要客观看待大模型的缺陷。

首先，大模型在某些感知方面不够精确，例如对空间的感知、精确坐标的感知，比如说让大模型数一数某些文本有多少个字数，这对他而言绝对是一个大挑战。

其次，大模型的感知途径还是太过于稀少。尽管现在已经有多模态大模型，但是人类的感知不仅仅是视觉和语言，还有听觉、触觉等等。大模型缺乏触觉，也许就难以让其把触觉相关的知识和某个物体联系起来。

最后，大模型的感知容量还是太小。尽管现在的大模型上下文长度达到了 \(10^5\)，甚至 \(10^6\) 级别，然而，如果我们想把海量的状态信息或者证据告诉大模型，可能存在着许多难度。这里的解决思路要么是扩大大模型的感知容量，要么就是延续“注意力机制”，让大模型精准锁定核心内容进行推理和思考。

尽管我们生活在一个内卷之上的时代，这也是一个科技每天翻天覆地革新的时代。很幸运我们能在 AI 大幅进步的浪潮中相遇，希望诸君在这片蓝海中，找到属于自己的机遇和价值。