笛卡尔树

换一种方式让我们学习笛卡尔树。

笛卡尔树是什么？

简单来说，给定一个序列 \(a_1,a_2,\dots,a_n\)，我们建立一个二叉堆，\(a_i\) 满足小根堆性质（大根堆也同理，本文以小根堆为例），而每个节点左儿子在序列中的编号小于其编号，右儿子编号大于其编号，如图（\(a\) 序列就是图中蓝色的序列，笛卡尔树建立方法如下）：

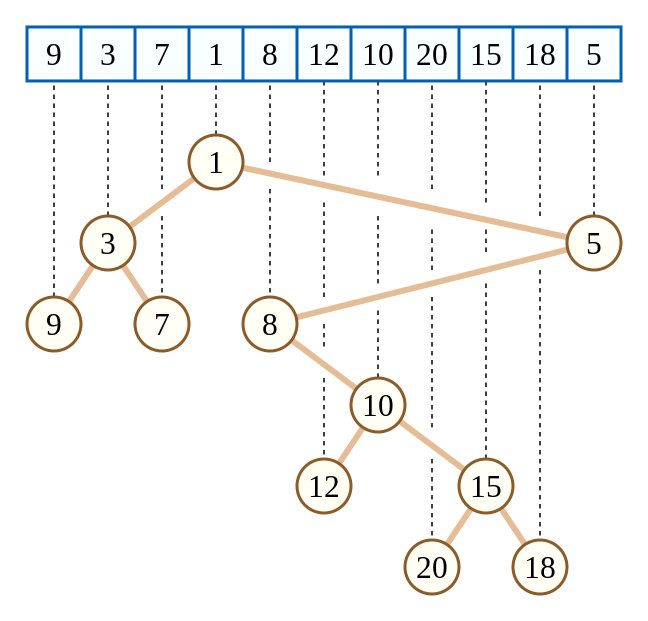
换个角度来看，观察这棵笛卡尔树的中序遍历（先访问左子树，再访问根结点，再访问右子树），可以发现其中序遍历就是原序列顺序。同时，这棵笛卡尔树又满足堆的性质。

所以我觉得可以给笛卡尔树一个第二定义：中序遍历为原序列的二叉堆。

那么我们也可以发现，如果把每个元素的下标 \(i\) 看成一维，把序列中的数字 \(a_i\) 看成一维，那么它就满足一种二维偏序关系，观察不难发现：其中 \(i\) 满足二叉搜索树性质，\(a_i\) 满足小根堆顺序。

例题

在讲解怎么写笛卡尔树之前，我们先看一个使用的例子（摘自 OI-wiki，原题 HDU 1506）。

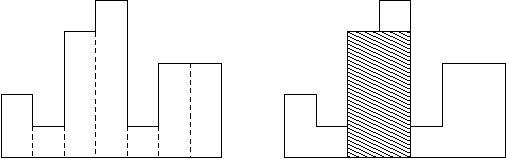
每个长条矩形宽度为 \(1\) 长度为 \(a_i\)，下端对齐，左右接在一起，问其中包含的最大矩形面积是多少。

先讲不用笛卡尔树的做法。

最朴素的暴力就是枚举左右端点，找打左右端点之间最小的 \(a_i\)（短板效应），然后用区间长乘以最小的 \(a_i\) 即可。时间复杂度 \(O(n^3)\)，用 st 表可以优化到 \(O(n^2)\)。

考虑优化决策，我们考虑每个 \(a_i\) 作为最小值的区间，那么以 \(a_i\) 作为最小值的答案就是区间长乘 \(a_i\)，在所有 \(a_i\) 作为最小值的答案中寻找最大的一个，就是所求答案。求解 \(a_i\) 作为最小值的区间可以使用单调栈优化，向左向右分别维护一次即可，代码如下：

const int N = 5e5+5;
int a[N],lef[N],rig[N];
void solve(int n) {
	rep(i,1,n) cin>>a[i];
	stack<int> stkl,stkr;
	rep(i,1,n) {
		while(stkl.size()&&a[stkl.top()]>=a[i]) stkl.pop();
		if(stkl.size()==0) lef[i]=1;
		else lef[i]=stkl.top()+1;
		stkl.push(i);
	}
	per(i,n,1) {
		while(stkr.size()&&a[stkr.top()]>=a[i]) stkr.pop();
		if(stkr.size()==1) rig[i]=n;
		else rig[i]=stkr.top()-1;
		stkr.push(i);
	} ll res=0;
	rep(i,1,n) res=max(res,1ll*a[i]*(rig[i]-lef[i]+1));
	cout<<res<<'\n';
}
signed main() {
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	while(true) {
		int n; cin>>n;
		if(n==0) exit(0);
		else solve(n);
	}
	return 0;
}

那么我们看一下笛卡尔树的定义，可以观察到，一个节点作为最小值的区间就是其子树所有结点的集合，那么，用笛卡尔树，每个结点的答案就是统计以每个节点子树中结点的个数乘该节点的权值，容易很多。

如何建树？

那么下面我们要解决的问题就是，如何建树。

回到题目，再回到单调栈做法，那么我们是不是可以参考单调栈的思路呢？显然是可以的。

考虑按照顺序依次插入 \(a_1,a_2,\dots a_n\)，那么这个节点一定是现存整棵树最靠右的节点（没有右儿子，并且只能是根或其他节点的右儿子），考虑用一个栈维护最靠右的那条链，观察它的性质。

这条链满足二叉搜索树性质，右儿子大于父亲，所以从根节点往下走一定单调递增。

那么，我们就可以考虑用一个栈维护右链，假如我们现在插入一个元素 \(a_i\)，我们要做的是，找到右链第一个大于于 \(a_i\) 的元素，设为 \(a_u\)，把 \(a_i\) 放在原本 \(a_u\) 的位置上，而原本的 \(a_u\) 作为 \(a_i\) 的左儿子即可。

代码如下：

int lc[N],rc[N],a[N],rt;
stack<int> stk;
void insert(int u) {
    int lst=-1;
    while(stk.size()&&a[stk.top()]>=a[u])
        lst=stk.top(),stk.pop();
    if(lst!=-1) lc[u]=lst;
    if(stk.size()!=0) rc[stk.top()]=u;
    else rt=u;
    stk.push(u);
}

回到题目，把笛卡尔树代码完善，并 dfs 统计子树大小即可，代码简单，如下：

const int N = 5e5+5, M = 1e6+5;
int lc[N],rc[N],a[N],rt,sz[N];
stack<int> stk;
void insert(int u) {
	lc[u]=rc[u]=0;
    int lst=-1;
    while(stk.size()&&a[stk.top()]>=a[u])
        lst=stk.top(),stk.pop();
    if(lst!=-1) lc[u]=lst;
    if(stk.size()!=0) rc[stk.top()]=u;
    else rt=u;
    stk.push(u);
}
void dfs(int u) {
	if(lc[u]) dfs(lc[u]);
	if(rc[u]) dfs(rc[u]);
	sz[u]=sz[lc[u]]+sz[rc[u]]+1;
}
void solve(int n) {
	while(stk.size()) stk.pop();
	rep(i,1,n) cin>>a[i],insert(i);
	dfs(rt);
	long long res=0;
	rep(i,1,n) {
		res=max(res,1ll*a[i]*sz[i]);
	} cout<<res<<'\n';
}
signed main() {
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	while(true) {
		int n; cin>>n;
		if(n==0) exit(0);
		else solve(n);
	}
	return 0;
}