斜率优化 dp
what is 斜率?
斜率,数学、几何学名词,是表示一条直线(或曲线的切线)关于(横)坐标轴倾斜程度的量。它通常用直线(或曲线的切线)与(横)坐标轴夹角的正切,或两点的纵坐标之差与横坐标之差的比来表示。
斜率又称“角系数”,是一条直线对于横坐标轴正向夹角的正切,反映直线对水平面的倾斜度。一条直线与某平面直角坐标系横坐标轴正半轴方向所成的角的正切值即该直线相对于该坐标系的斜率。如果直线与 \(x\) 轴互相垂直,直角的正切值为 \(\tan {\pi\over2}\),故此直线不存在斜率(也可以说直线的斜率为无穷大)。当直线L的斜率存在时,对于一次函数 \(f(x)=kx+b\)(斜截式),\(k\) 即该函数图像的斜率。
那么如果给定两个点 \(a\) 和 \(b\),他们在平面直角坐标系中的坐标分别为 \((x_a,y_a)\) 和 \((x_b,y_b)\),令 \(x_b-x_a>0\),两点连线的斜率 \(k=\frac{y_b-y_a}{x_b-x_a}\)
引入题
平面中有 \(n\) 个点 \((x_i,y_i)\),有 \(q\) 条直线,斜率 \(k\) 已经确定,需要在给定的 \(n\) 个点中,选出一个点 \((x,y)\),使得 \(kx+y\) 最大(\(n,q\in[1,2\times 10^5]\))。
这道题最好画一个图,有助于解题。
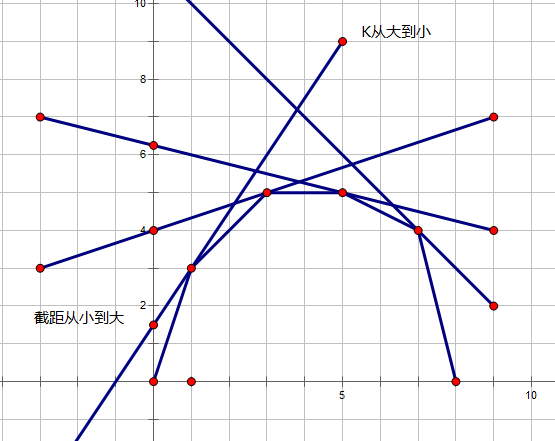
先看表达式:\(kx+y\)。如果把 \(k\) 取个相反数,那么就是直线的表达式,所得到的值就是截距。那么就只要维护一个上凸包(后文会解释)即可。
因为题目中的式子,所以在图中的斜率正负是相反的,也就是斜率从大到小来,通过看图,可以知道,这张图基本上可以证明、维护上凸包切点的做法正确性是显然的。
注意:图中的斜率和题目中的 \(k\) 是相反数。
- 考虑哪些点可能作为决策点(可能作为最大值的点)?
对于两点 \((x_1,y_1)\)、\((x_2,y_2)\),并且 \(x_1<x_2\),假设点 \((x_2,y_2)\) 比更优 \((x_1,y_1)\),那么:
(\(k_{i\sim j}\) 表示第 \(i\) 个点与第 \(j\) 个点之间连线的一次函数斜率)
对于该此询问的 \(k\),一个点只有比左右两个相邻的点都更优,它才能成为决策点,所以我们将所有点按照 \(x\) 坐标进行排序。
如果点 \(i\) 能成为决策点,对于他的左右相邻的点为 \(i-1\) 和 \(i+1\),可以推出 \(k_{{1\sim i-1}\geq i\sim i+1}\),所以要求 \(k_{1\sim i-1}<k_{i\sim i+1}\),所以后一条线段的斜率小于前一条线的斜率,所以必须是一个上凸包(如下图)。

如果此题在线,可以考虑对于任意一个点的加入,将由于其加入,而不能作为决策点的点删除,可发现,我们的目的是维护上凸包,保留两点间斜率依次递减的点。
- 那么对于前 \(m\) 个点,如何维护决策点点集?
前 \(i\) 个点作为决策点的点集,一定被包含于前 \(i-1\) 个点作为决策点的点集于第 \(i\) 个点的并,也就是说如果讲 \(A_i\) 定义为前 \(i\) 个点作为决策点的点集,那么用符号与研究可以表示为:
用类单调栈的算法维护,从现有点集的栈依次考虑,若栈顶元素与栈中之前的点形成的是下凸包,那么将其退栈,直到找到可以与栈中其他点构成上凸包的第一个点,结束本轮退栈操作,\(A_i\) 求解完毕(这个过程也可以理解为一个变态的单调栈)。
简而言之就是:遇到一个点 \(i\) 先将其与队末连线,如果产生了一个下凸包,则删掉原本队末元素,直至满足条件。然后加入 \(i\) 点,那么可以保证其与前队中原有点的连线仍然是一个上凸包。
最终所有栈中决策点的连线一定形如下图,也就是一个有多个点构成的大上凸包:
时间复杂度 \(O(n)\)(证明:因为每个数都最多加入一次,删除一次)
这样,我们就维护出了前 \(i\) 个点的中合法决策点的点集。
- 对于每次寻问,给出一个固定的 \(k\),那个点能成为全局最大值(最优决策点)呢?
那么也就要求,其前一个点必定比它劣,后一个点也比它劣。
我们令 \(j\) 为栈中的点的编号,\(k_j\) 表示第 \(j\) 个点与其前驱之间的连线斜率。
也就是说,对于全局最优点 \(j\),对于 \(\forall l\leq j\),\(k_l\geq -k\),对于 \(\forall l> j\),\(k_l\leq -k\),可以通过开头的证明,易得在如此情况下,\(j\) 是最优点。
性质:点 \(j\) 是全局最优决策点,等价于 \(k_j>-k\) 且 \(k_{j+1}\leq -k\)。
易发现其满足单调性,容易想到二分算法,只需要在合法决策点点集中进行二分,就可以求得最优的决策点编号和答案。
代码如下:
#include <bits/stdc++.h>
#define int long long
#define double long double
#define x first
#define y second
using namespace std;
const int N = 5e5 + 5;
pair<int, int> pt[N];
// pt[i].x 记录第 i 个点的 x 坐标,pt[i].y 记录其 y 坐标
double getslp(int x1, int y1, int x2, int y2) {
if(x2-x1==0) return 2e18;
// 注意:若 x2-x1 为 0,那么无法进行除法,返回 inf
double res = (double)(y2 - y1) / (double)(x2 - x1);
return res;
} // 求两点连线的斜率
main() {
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; ++i) cin >> pt[i].first >> pt[i].second;
sort(pt + 1, pt + n + 1);
stack<pair<double, int>> stk;
// stk 利用 stl 的 stack 实现栈
stk.push(make_pair(3e18, 1));
for (int i = 2; i <= n; ++i) {
while (stk.size()) {
// 如果这一个结点与栈中上一个节点的连线会形成下凸包
// 那么将这个点从栈中删除
// 否则,这个点和栈中上一个节点形成上凸包,停止退栈
double slplst = stk.top().x;
int id = stk.top().y;
double slpnow = getslp(pt[id].x, pt[id].y, pt[i].x, pt[i].y);
// 通过比较 slpnow 和 slplst 的大小关系判断凸包情况
if (slpnow < slplst) {
stk.push(make_pair(slpnow, i));
break; // 上凸包,循环结束
}
if(stk.size()>1) stk.pop(); //下凸包,退栈
}
}
vector<pair<double, int>> vc;
// vc 为决策点点集
while (stk.size()) {
vc.push_back(stk.top());
stk.pop();
} // 栈中最后的元素就是决策点点集
for (int i = 1; i <= m; ++i) {
int slp;
cin >> slp;
// 对于每次输入,二分查找 -k 点集的位置
int lef = 1, rig = vc.size() - 2;
while (lef <= rig) {
int mid = lef + rig >> 1;
if (vc[mid].x < -slp)
lef = mid + 1;
else
rig = mid - 1;
}
int res = -2e18;
if (lef >= 0 && lef < vc.size())
res = max(res, pt[vc[lef].y].x * slp + pt[vc[lef].y].y);
if (rig >= 0 && rig < vc.size())
res = max(res, pt[vc[rig].y].x * slp + pt[vc[rig].y].y);
lef = 0;
res = max(res, pt[vc[0].y].x * slp + pt[vc[0].y].y);
rig = vc.size() - 1;
res = max(res, pt[vc[vc.size() - 1].y].x * slp + pt[vc[vc.size() - 1].y].y);
// 这里,由于逻辑混乱,不如牺牲一些常数,保证答案正确性
cout << res << '\n';
// 输出答案
}
return 0;
}
令 \(q=n\),易得总时间复杂度为 \(O(n\log n)\)。
- 如何继续优化时间复杂度?
从几何上理解:

假设一条斜率为 \(-k\) 的直线,从 \(y\) 轴正方向,远离 \(x\) 轴的地方逐渐向凸包连线递减,直到与任意凸包相切,可以发现随着 \(-k\) 的逐渐变小,相切点逐渐向 \(x\) 轴正方向移动,那么我们可以按照 \(-k\) 从大到小进行排序,利用单指针从左向右扫描,可以 \(O(n)\) 求出答案。
代码如下:
#include <bits/stdc++.h>
#define int long long
#define x first
#define y second
using namespace std;
const int N = 1e5 + 5;
pair<int, int> pt[N];
pair<int, int> slp[N];
// slp[i].x 记录询问的斜率,slp[i].y 记录每次询问的编号,方便排序后寻找原顺序输出答案
int res[N];
// 记录答案的数组
double getslp(int x1, int y1, int x2, int y2) {
if(x2-x1==0) return 2e18;
double res = (double)(y2 - y1) / (double)(x2 - x1);
return res;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; ++i) cin >> pt[i].first >> pt[i].second;
sort(pt + 1, pt + n + 1);
stack<pair<double, int>> stk;
stk.push(make_pair(3e18, 1));
for (int i = 2; i <= n; ++i) {
while (stk.size()) {
double slplst = stk.top().x;
int id = stk.top().y;
double slpnow = getslp(pt[id].x, pt[id].y, pt[i].x, pt[i].y);
if (slpnow < slplst) {
stk.push(make_pair(slpnow, i));
break;
}
if(stk.size()>1) stk.pop();
}
}
vector<pair<double, int>> vc;
vc.push_back(make_pair(-9e18, 0));
while (stk.size()) {
vc.push_back(stk.top());
stk.pop();
} //以上代码与 n log n 版本相同
for(int i = 1; i <= m; ++i) cin >> slp[i].x, slp[i].y = i;
sort(slp + 1, slp + m + 1);
//对于所有输入的斜率进行排序
int id = vc.size()-1;
// 指针一开始指向决策点点集末尾
for(int i = 1; i <= m; ++i) {
while(vc[id - 1].x > -slp[i].x) --id;
// 将指针 tp 不断向前移动
res[slp[i].y] = pt[vc[id].y].x * slp[i].x + pt[vc[id].y].y;
// 记录答案
}
for(int i = 1; i <= m; ++i) cout << res[i] << '\n';
// 输出答案
return 0;
}
如何用其优化 dp?
设 dp 状态 \(f_{i,j}\) 为前 \(i\) 个数字,分成 \(j\) 段的最小方差。
很容易得到一个朴素的状态转移方程:\(f_{i,j,}=\min\limits_{k=1}^i\{f_{k,j-1}+cost(k+i,j)\}\)。
这样的时间复杂度是 \(O(n^3)\) 的,不可过。
所以,dp 数组表示方差的方案难以优化,是不可行的,我们需要用其他方式转化方差:
令 \(p\) 等于序列平均数 \(p=\frac{{\sum_{i=1}^n}a_i}{n}\),\(S\) 为方差,\(n\) 为数组长度,\(a_i\) 为数组的第 \(i\) 个元素。
将 \({p=\frac{{\sum_{i=1}^n}a_i}{n}}\) 代入,
利用前缀和,令 \(q_i={\sum}_{j=1}^i a_j\)。
可将上式转化为 \(S=\frac{{\sum_{i=1}^n} {a_i}^2}{n}-\frac{{q_n}^2}{n^2}\)。
可以发现:多项式第一项 \(\frac{{\sum_{i=1}^n} {a_i}^2}{n}\) 是常数,只要考虑第二项 \(\frac{({\sum_{i=1}^n}a_i)^2}{n^2}\) 即可。
这样,令 \(f_{i,j}\) 表示前 \(i\) 个数分成 \(j\) 段的最小平方和,我们就可以得到一个状态转移方程:
容易发现 \(j\) 可以作为 dp 的阶段,在 \(j\) 固定时从小到大枚举 \(i\),在 \(i\) 固定时从小到大枚举 \(k\),这样直接做还是 \(O(n^3)\) 的,考虑优化掉决策 \(k\) 的枚举.
在 \(j,i\) 固定时,对式子进行变形,分离变量:
在枚举 \(i\) 的时候,我们实际是在查询 \(f_{j-1}\) 这一维里前 \(i-1\) 个数中 \(f_{k,j-1}+q_{k}^2-2q_{i}\times q_{k}\) 这个式子的最小值.
这是一个 \((\)常量 \(\times\) 变量 \(+\) 变量\()\) 形的转移,符合斜率优化的结构,令 \(k=-2q_{i},x=q_{k},y=f_{k,j-1}+q_{k}^2\),这就转化为了每次添加一个点,查询 \(kx+y\) 的最小值,且 \(k=-2q_{i}\) 单调递减.
这就是斜率优化引入题的变式,利用上一题的结论维护凸包与最优决策点即可过掉这一题.
推式子过程,若用 \(k_1\) 比 \(k_2\) 转移更优,则:
上式于是成为了一个标准的斜率优化式,然后使用斜率优化即可,而且显而易见的,可以使用滚动数组压缩掉一维空间。
可写出代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 3007;
int a[N], q[N];
int f[N], pf[N];
int p[N];
int check(int x, int y) {
return (pf[y] - pf[x] + q[y] * q[y] - q[x] * q[x]) / (q[y] - q[x]);
}
int main() {
int n, m;
cin >> n >> m;
q[0] = 0;
for (int i = 1; i <= n; ++i)
cin >> a[i], q[i] = q[i - 1] + a[i];
for (int i = 1; i <= n; ++i)
pf[i] = q[i] * q[i];
int l, r;
for (int i = 2; i <= m; ++i) {
l = r = 1, p[l] = i - 1;
for (int j = i; j <= n; ++j) {
while (l < r && check(p[l], p[l + 1]) < 2 * q[j]) l++;
f[j] = pf[p[l]] + (q[j] - q[p[l]]) * (q[j] - q[p[l]]);
while (l < r && check(p[r - 1], p[r]) > check(p[r], j)) r--;
p[++r] = j;
}
for (int j = 1; j <= n; ++j) pf[j] = f[j];
}
cout << m * f[n] - q[n] * q[n];
return 0;
}
总结
- 可以在写题前先考虑朴素算法,再进行优化;
- 斜率优化难度不大,主要在于推式子,推出式子后,可以用一个单指针或者双指针的做法优化转移;
- 小技巧:查询最大值维护上凸包,斜率递减;查询最小值维护下凸包,斜率递增;至于决策点如何移动根据几何直观看切点即可减少很多思维量。
- 多练习推式子和斜率优化 dp,纸上得来终觉浅,绝知此事要躬行!




 浙公网安备 33010602011771号
浙公网安备 33010602011771号