高精度

\(1.\) 介绍

高精度是一种广为人知的算法，它所涉及的范围是大数与大数之间的运算。

在我们平时做题中有时会遇到几十位，几百位这样的数之间进行加减乘除等运算。

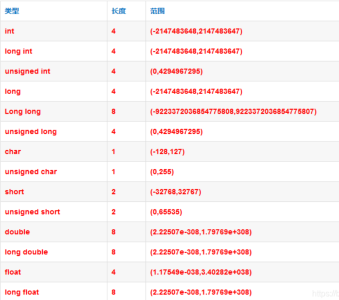
见上表，我们所熟知的 \(long \quad long\) 和 \(double\) 类型都已经存不下了，这时候，我们就需要引入一个新的算法，叫做高精度算法。

\(2.\) 思想

高精度算法本质上是用字符串模拟数字进行计算，利用类似于数学里的竖式的形式，一位一位的进行计算。

\(3.\) 代码及其原理

这里我们列了一个竖式，计算的是 \(12+68\) 。

我们可以定义 \(a,b\) 两个数组，用来按位存放每一个数字。

这个竖式就可以这样存：

a[1]=2,a[2]=1
b[1]=8,b[2]=6

这里是倒序存储，这样有助于我们进行计算。

之后，我们可以写核心代码了，算法描述如下：

int c[10001];
void ad(int a[],int b[]){
	int i=1,jw=0;
	while((i<=len(a))||(i<=len(b))){
		c[i]=a[i]+b[i]+jw;//第i位相加并加上上一位的进位
		jw=c[i]/10;//高位进位
		c[i]%=10;//存储第i位的值
		i++;
	}
}

完整代码如下：

#include <iostream>
#include <cstdio>
#include <fstream>
#include <algorithm>
#include <cmath>
#include <string>
#include <cstring>
using namespace std; 
int a[1001],b[1001],c[1001]={0};
int main()
{
	string s1,s2;
	cin>>s1>>s2;
	int len1=s1.size();
	int len2=s2.size();
	int lenc=max(len1,len2);
	for(int i=0;i<=len1-1;++i){
		a[i]=s1[len1-1-i]-'0';
	}
	for(int i=0;i<=len2-1;++i){
		b[i]=s2[len2-1-i]-'0';
	}
	int jw=0;
	for(int i=0;i<=lenc-1;++i){
		c[i]=a[i]+b[i]+jw;
		if(c[i]>=10){
			jw=1;
			c[i]=c[i]%10;
		}
		else{
			jw=0;
		}
	}
	if(jw!=0){
		c[lenc]=1;
		lenc++;
	}
	int len=lenc-1;
	while(c[len]==0&&len>=1){
		len--;
	}
	for(int i=len;i>=0;--i){
		cout<<c[i];
	}
    return 0;
}

而减法，乘法和除法的运算过程也是同理，都是运用竖式的思想来解决的。

//减法
int jw=0;
		for(int i=0;i<=len1-1;++i){
	    if(a[i]<b[i]){
	        jw=10;
	        a[i+1]--;
	        c[i]=jw+a[i]-b[i];
		}
		else{
			jw=0;
			c[i]=a[i]-b[i];
		}
    }

//乘法
for(int i=0;i<=len2-1;++i){
		for(int j=0;j<=len1-1;++j){
			c[i+j]+=b[i]*a[j]; 
			if(c[i+j]>=10){
				c[i+j+1]+=c[i+j]/10;
				c[i+j]=c[i+j]%10;
			}
		}
	} 

//除法
for(int i=1;i<=len1;++i){//按位相除 
	c[i]=(jw*10+a[i])/b;
	jw=(jw*10+a[i])/b;
}

\(4.\) 建议

高精度算法是每个初学者必会的算法，它可以和其他算法组合起来解决一些数据范围较大的题目。