间断检测(一)
间断检测
对一个下图所示的 3×3 模板,这一过程包括计算模板所包围区域内灰度级与模板系数的乘积之和。就是说,在图像中任意点的模板响应由下列公式给出:
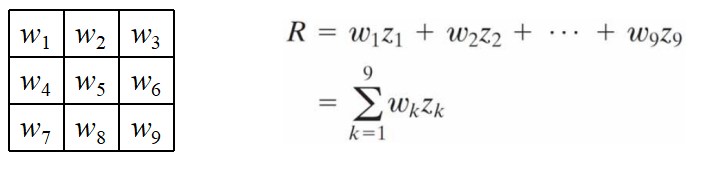
这里,zi 是与模板系数 wi 相联系的像素的灰度级。模板的响应定义是相对于它的中心位置。
点检测
基本思想:如果一个孤立的点(此点的灰度级与其背景的差异相当大,并且它所在的位置是一个均匀的或近似均匀的区域)与它周围的点很不相同,则很容易被这类模板检测到。
如下模板:

上述又为拉普拉斯模板。针对点的检测。
代码实例
clear;clc; f = imread('dot2.png'); f1=rgb2gray(f); w = [-1 -1 -1;-1 8 -1;-1 -1 -1]; % 点检测掩模 g = abs(imfilter(double(f1),w,'conv')); g=g(5:488,5:490); T = max(max(g(:))); g = g>=(T.*0.3); subplot(1,3,1);imshow(f);title('原图像'); %subplot(1,3,2);imshow(g2);title('原图像'); subplot(1,3,3);imshow(g);title('点检测');

线检测
下面四个模板分别对4个方向上单像素宽的线有最大响应。
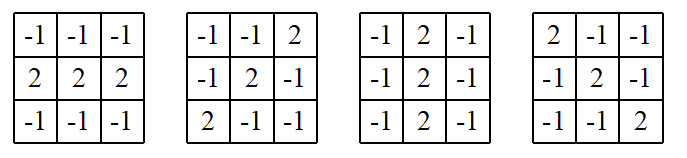
令 R1、R2、R3、R4 代表图中从左到右模板的响应,分别对应检测水平,45°,垂直,-45°(x轴垂直向下)。假设4个模板分别应用于一幅图像,在图像中心的点,如果 |Ri|>|Rj|,j≠i,则此点被认为与模板 i 方向的线更相关。 如果只检测特定方向上的线,我们应使用与这一方向有关的模板,并设置该模板的输出门限。
例子
特定方向上的线检测 图:一幅电路接线模板的数字化(二值)图像。假设我们要找到一个像素宽度的并且方向为-45°的线条。基于这个假设,使用上图中最后一个模板。
原图像:

代码
clear;clc; f = imread('lineDetect.png'); f=rgb2gray(f);% 图像大小 w = [2 -1 -1;-1 2 -1;-1 -1 2]; % 45°方向检测线 g = imfilter(double(f),w); gtop = g(1:120,1:120); % 左上角区域 gtop = Zoom(gtop,4); % 通过复制像素将图像扩大gtop*4倍 gbot = g(end-119:end,end-119:end); % 右下角区域 gbot = Zoom(gbot,4); g1 = abs(g); % 检测图的绝对值 T = max(g1(:)); g2 = g1>=T; subplot(3,2,1);imshow(f);title('原图像'); subplot(3,2,2);imshow(g,[]);title('线检测-45°方向'); subplot(3,2,3);imshow(gtop,[]);title('左上角区域'); subplot(3,2,4);imshow(gbot,[]);title('右下角区域'); subplot(3,2,5);imshow(g1,[]);title('图像绝对值'); subplot(3,2,6);imshow(g2);title('g>=T');
Zoom为运用双线性插值法对图像进行放大:
function [I_out] = Zoom(I_in,tn) %UNTITLED14 此处显示有关此函数的摘要 % 此处显示详细说明 % 首先读入需要放大的灰度图像 m = size(I_in,1); % 获取原图像大小 n = size(I_in,2); T = [tn,0,0;0,tn,0;0,0,1]; % 仿射矩阵T % 定义输出图像 I_out I_out = ones(m*tn,n*tn); for i = 1:m*tn % 从图像的左上角开始遍历输出图像 for j = 1:n*tn % 输出图像像素坐标反向映射得到输入图像像素坐标x和y z = [i,j,1]/T; x = z(1); y = z(2); % 下面判断反向映射得到的坐标(x, y)是否超出输入图像的大小, % if条件成立则没有超出, % 条件不成立则不进行任何操作,定义I_out时已经默认该点灰度为1 if (x>=1 & y>=1) & (x<=m & y<=n) % 然后再判断x或y是否为小数,if条件成立则是小数 if (rem(x,1))||(rem(y,1)) % 坐标为小数则需要插值 % 先获取该小数坐标(x, y)邻近的四个像素坐标 x0 = floor(x); x1 = ceil(x); y0 = floor(y); y1 = ceil(y); % 获取邻近坐标的灰度值 a = I_in(x0,y0); b = I_in(x0,y1); c = I_in(x1,y0); d = I_in(x1,y1); % 双线性内插 g1 = a + (x-x0) * (c - a); g2 = b + (x-x0) * (d - b); I_out(i,j) = g1 + (y - y0) * (g2 - g1); else % x和y都为整数则直接赋予原图像的灰度值 I_out(i,j) = I_in(x,y); end end end end % 显示原图像和放大后的输出图像 %figure;imshow(I); %figure;imshow(I_out);end

从上方,我们可以看到左上角和右下角的线宽不一样,说明我们可以运用特定大小的模板来对图像进行特定线宽的先检测。
下面,采用5*5的梯度模板:

可见模板过大,效果变坏。
边缘检测
一条理想的边缘具有如图所示模型的特性。依据这个模型生成的完美边缘是一组相连的像素的集合(此处为在垂直方向上),每个像素都处在灰度级跃变的一个垂直的台阶上(如图形中所示的水平剖面图)。
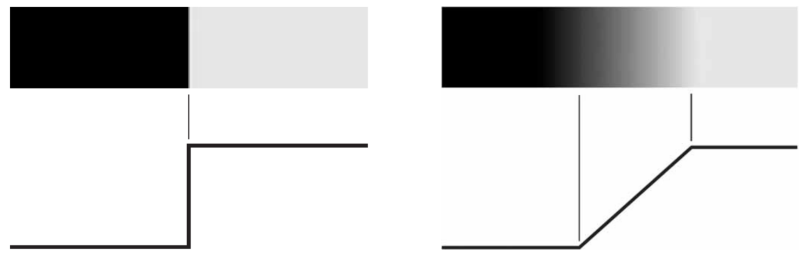
实际上,光学系统、取样和其它图像采集的不完善性使得到的边缘是模糊的,边缘被模拟成具有“类斜面”的剖面.
在有噪声的边缘附近的一阶和二阶导数性质:
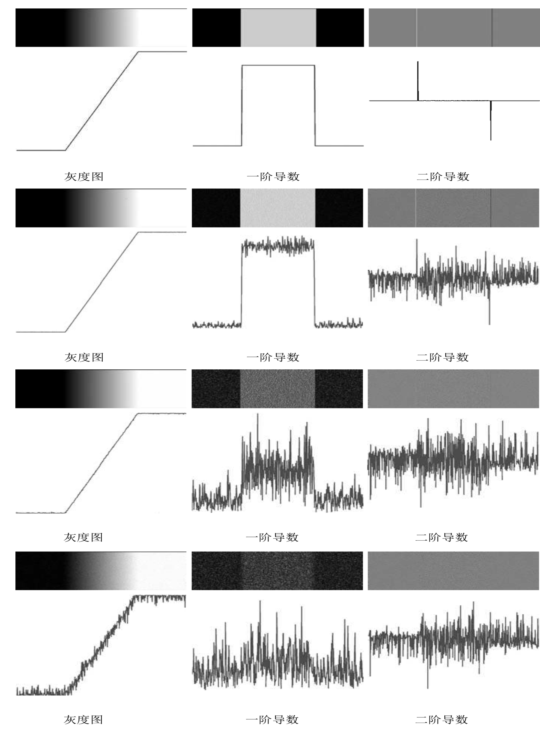
第1列第1幅图像无噪声,其它3幅分别被附加的零均值且标准差为0.1、1.0和10.0灰度级的高斯噪声污染了。 每幅图像下面显示的图是穿过图像的水平扫描线的灰度级剖面线。 第2列图像:左边图像的一阶导数图像 第3列图像:二阶导数图像.
我们可以得出这样的结论:为了对有意义的边缘点进行分类,与这个点相联系的灰度级变化必须比在这一点的背景上的变化更为有效。 由于我们用局部计算进行处理,决定一个值是否有效的选择方法就是使用门限。因此,如果一个点的二维一阶导数比指定的门限大,我们就定义图像中的此点是一个边缘点。 如果我们选择使用二阶导数,则另一个可用的定义是将图像中的边缘点定义为它的二阶导数的零交叉点。
边缘检测:梯度算子
一幅数字图像的一阶导数是基于各种二维梯度的近似值。图像 f(x, y) 在位置 (x, y) 的为下列向量:
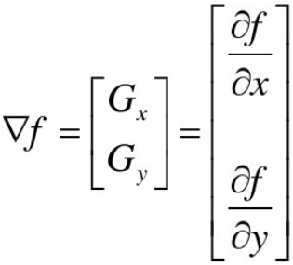
在边缘检测中,一个重要的量是这个向量的大小
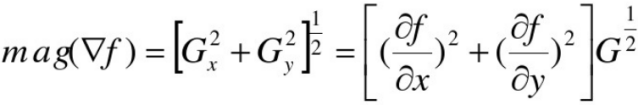
这个量给出了在 ∇f 方向上每增加单位距离后 f(x, y) 值增大的最大变化率。一般来讲也将 ∇f 称为梯度(尽管并不完全正确).
梯度向量的方向也是一个重要的量。令 α(x, y) 表示向量 ∇f 在 (x, y) 处的方向角。然后,由向量分析得到:
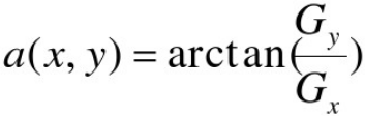
角度是以 x 轴为基准度量的。边缘在 (x, y) 处的方向与此点的梯度向量的方向垂直。 比较常见的计算梯度分量的方法是利用一些空间域的模板。
三种梯度算子
Roberts(罗伯特)交叉梯度算子(2*2维)

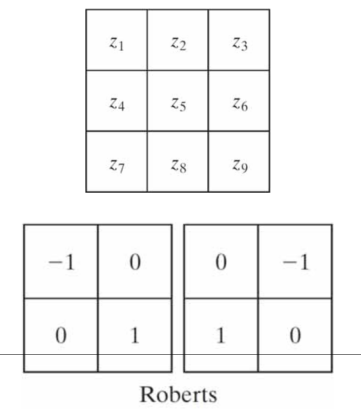
Prewitt(普鲁伊特)算子(3*3维)
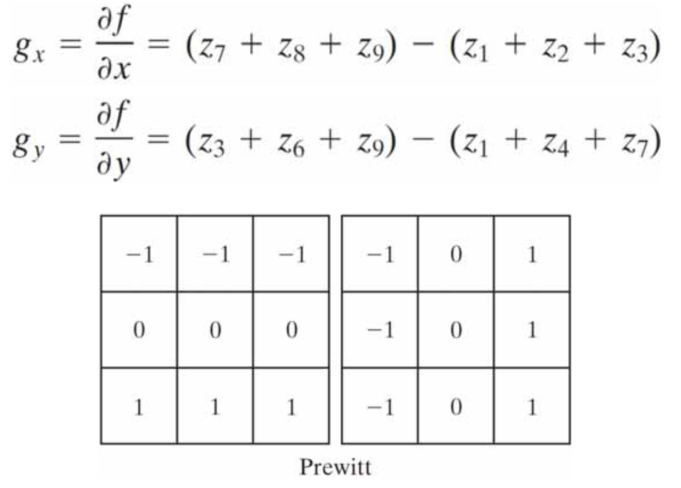
Sobel(索贝尔)算子(3*3)
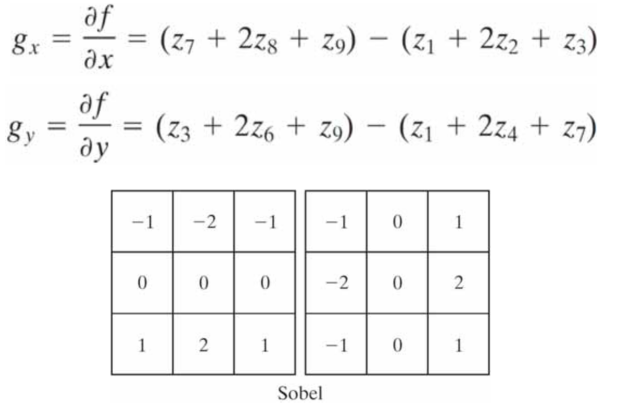
Prewitt和Sobel算子是在实践中计算数字梯度时最常用的。Prewitt模板实现起来比Sobel模板更为简单,但后者在噪声抑制特性方面略优。
对角线的模板
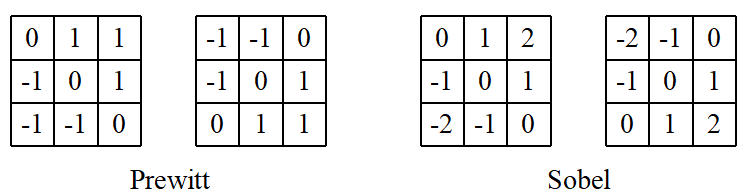
Prewitt算子结果:
img=imread('house.png'); [M,N,K]=size(img); %定义模板 model=[0 1 1;-1 0 1;-1 -1 0]; img_result=zeros(M,N,K); %预生成 model_size=3; %模板尺寸 expand_size=floor(model_size/2);%提高速度 for k=1:3 for i=1:M for j=1:N expand_img=double(wextend('2D','zpd',img(:,:,k),expand_size));%扩展0,也就是增加padding ave=sum(sum(expand_img(i:i+model_size-1,j:j+model_size-1).*model)); img_result(i,j,k)=ave; end end end img_result=uint8(img_result); subplot(1 ,2, 1); title('原图像') imshow(img) subplot(1 ,2, 2); imshow(img_result) da = ['模板大小为' num2str(model_size) ',变化后的图像']; title(da)

a=imread('house.png'); I=rgb2gray(a); BW1=edge(I,'Roberts',0.16); BW2=edge(I,'Sobel',0.16); BW3=edge(I,'Prewitt',0.06); BW4=edge(I,'LOG',0.012); BW5=edge(I,'Canny',0.12); figure('Name','进行五种边缘检测'); subplot(2,3,1);imshow(I);title('原图'); subplot(2,3,2);imshow(BW1);title('Robert算子边缘检测') subplot(2,3,3);imshow(BW2);title('Sobel算子边缘检测') subplot(2,3,4);imshow(BW3);title('Prewitt算子边缘检测'); subplot(2,3,5);imshow(BW4);title('LOG算子边缘检测'); subplot(2,3,6);imshow(BW5);title('Canny边缘检测');

未完.......待下一篇


 浙公网安备 33010602011771号
浙公网安备 33010602011771号