创建及遍历树

　　对于树的创建，及前序，中序，后序遍历。

　　小编创建时，全部采用new 动态创建内存的方式。（小编对于定义啥的，有点懵，涉及到内存存活时间和作用域的问题，姑且先动态分配内存）

 　　按照满二叉树创建：

//按照满二叉树链表创建  返回指向根节点的指针变量  自上而下 自左而右
BTNode* Create_BTree(void)
{
    BTNode* T, * p, * s[MAX_NODE];
    char ch; int i, j;
    T = new BTNode;
    while (true)
    {
        cout << "请输入i（0代表结束创建过程）：" << endl;
        cin>>i;
        if (i == 0)break;
        else {
            cout << "请输入字符" << endl;
            cin.get(ch); cin.get(); p = new BTNode;
            p->data = ch;
            p->Lchild = p->Rchild = NULL; s[i] = p;
            if (i == 1)T = p;
            else
            {
                j = ceil(i / 2);
                if (i % 2 == 0)s[j]->Lchild = p;
                else s[j]->Rchild = p;
            }
        }
    }
    return T;
}

　　关于扩充二叉树：

　　原本的叶子节点后面多了个新的单元，data为‘？’。

//按照先序遍历方式 建立
BTNode * Preorder_Create_BTree(BTNode* T)
{
    char ch;
    cout << "Please input a char:" << endl;
    cin.get(ch); cin.get();
    if (ch == '?')
    {
        T->data='?';
        T->Lchild = NULL;
        T->Rchild = NULL;
        return T;
    }
    else
    {
        T->data = ch;
        T->Lchild = new BTNode;
        T->Rchild = new BTNode;
        Preorder_Create_BTree(T->Lchild);
        Preorder_Create_BTree(T->Rchild);
        return T;
    }
}

　　下面分别是前序，中序，后序的访问：

struct BTNode
{
    char data;
    struct BTNode* Lchild, * Rchild;
};
//DLR先序遍历（根节点 左 右）  LDR中序遍历  LRD后序遍历
//分别讨论递归算法和非递归算法
const void visit(char T)
{
    cout << T << ' ';
}
void PreorderTranspose1(BTNode* T)
{
    if (T->data != '?')
    {
        visit(T->data);
        PreorderTranspose1(T->Lchild);
        PreorderTranspose1(T->Rchild);
    }
}
//中序遍历   左 根 右
void InorderTraverse1(BTNode* T)
{
    if (T->data != '?')
    {
        InorderTraverse1(T->Lchild);
        visit(T->data);
        InorderTraverse1(T->Rchild);
    }
}
//后序遍历 左 右 根
void PostorderTraverse1(BTNode* T)
{
    if (T->data != '?')
    {
        PostorderTraverse1(T->Lchild);
        PostorderTraverse1(T->Rchild);
        visit(T->data);
    }
}

 求叶子节点树和深度：

针对扩展树，求的叶子节点正是‘？’。

//求二叉树的叶子节点数     先找的左下的叶子节点
int search_leaves(BTNode* T)
{
    BTNode* Stack[MAX_NODE], * p = T;
    int top = 0, num = 0;
    if (T->data!='?')
    {
        Stack[ ++top ] = p;
        while (top > 0)
        {
            p = Stack[top--];    //当节点左右节点都是NULL时，Stack中这个节点位置都会被左节点替代,从而跨越到本届点的右边
            if (p->Lchild == NULL && p->Rchild == NULL) num++;
            if (p->Rchild != NULL)
                Stack[++top] = p->Rchild;
            if (p->Lchild != NULL)
                Stack[++top] = p->Lchild;
        }
    }
    return num;
}
//求二叉树的深度  利用层次遍历法可以直接求二叉树的深度
int search_depth(BTNode* T)
{
    BTNode* Queue[MAX_NODE], * p = T;
    int front = 0, rear = 0, depth = 0, level;
    if (T->data!='?')
    {
        Queue[++rear] = p;
        level = rear;
        while (front < rear)
        {
            p = Queue[++front];
            if (p->Lchild != NULL)
                Queue[++rear] = p->Lchild;
            if (p->Rchild != NULL)
                Queue[++rear] = p->Rchild;
            if (front == level)
            {
                depth++; level = rear;
            }
        }
    }
    return depth;
}

 　　此时，我们通过判定左右子树是否为空来判定叶子节点的范围。小编代码中全部通过动态内存创建的BTNode，所以也会包含进来。

　　

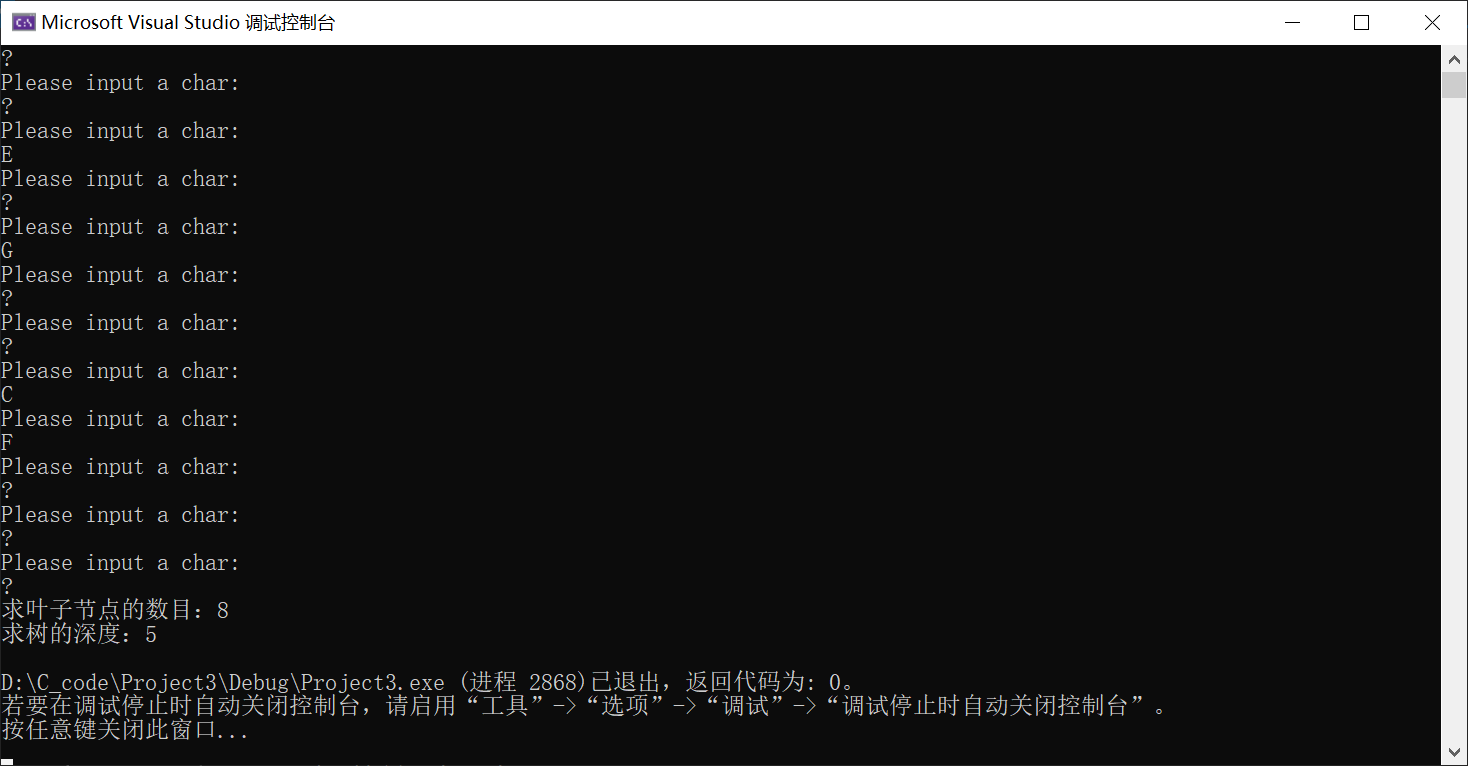
　　如果想要忽略‘？’对求解叶子节点以及深度的影响，代码可以更改如下：

　　通过判定左右节点data数据是否为‘？’来判定叶子节点。

//求二叉树的叶子节点数     先找的左下的叶子节点
int search_leaves(BTNode* T)
{
    BTNode* Stack[MAX_NODE], * p = T;
    int top = 0, num = 0;
    if (T->data!='?')
    {
        Stack[ ++top ] = p;
        while (top > 0)
        {
            p = Stack[top--];    //当节点左右节点都是NULL时，Stack中这个节点位置都会被左节点替代,从而跨越到本届点的右边
            if (p->Lchild->data == '?' && p->Rchild->data == '?') num++;
            if (p->Rchild->data != '?')
                Stack[++top] = p->Rchild;
            if (p->Lchild->data != '?')
                Stack[++top] = p->Lchild;
        }
    }
    return num;
}
//求二叉树的深度  利用层次遍历法可以直接求二叉树的深度
int search_depth(BTNode* T)
{
    BTNode* Queue[MAX_NODE], * p = T;
    int front = 0, rear = 0, depth = 0, level;
    if (T->data!='?')
    {
        Queue[++rear] = p;
        level = rear;
        while (front < rear)
        {
            p = Queue[++front];
            if (p->Lchild->data != '?')
                Queue[++rear] = p->Lchild;
            if (p->Rchild->data != '?')
                Queue[++rear] = p->Rchild;
            if (front == level)
            {
                depth++; level = rear;
            }
        }
    }
    return depth;
}