Huffman树和其编码

　　小编最近学习了Huffman树，特此记录一下。

　1 不过，我们首先来介绍一下 线索树。

　　线索树 n个节点的二叉树 n-1条指针线，n个节点右2n个指针域，右n+1个空闲指针，利用这些空闲指针来存放直接前驱和直接后继信息。

　　若节点右左孩子：则Lchild指向左孩子，否则指向直接前驱。
　　若节点由右孩子：则Lchild指向右孩子，否则指向直接后继。
　　我们增加两个标致域 Ltag：0 指向左孩子 1 指向前驱 Rtag：0指向右孩子 1 指向直接后继线索链表  按照某种次序遍历，加上线索的二叉树叫线索二叉树。

　　相关的定义：

typedef struct BiThrNode
{
    elemtype data;
    struct BiThrNode* Lchild, * Rchild;
    int Ltag, Rtag;
}BiThrNode;
typedef struct listnode
{
    int childno;
    struct listno* next;
}CTNode;
typedef struct
{
    elemtype data;
    CTNode* fistchild;
}HNode;
typedef struct
{
    HNode nodes[MAX_NODE];
    int root;
    int num;
}CLinkList;
//孩子兄弟表示法（二叉树表示法）   两个指针域，分别指向节点的第一个子节点和下一个兄弟节点
//和二叉树的 左右节点类似
typedef struct CSnode
{
    elemtype data;
    CSnode* firstchild, * nextchild;
}CSNode;
//树转换成二叉树
//1 加虚线 在树的每层按从左至右的数需在兄弟节点之间加上虚线
//2 去连线 除最左边的第一个子节点之外，父节点与其所有其他子节点的连线都去掉
//3 旋转 将树顺时针旋转45  原有实线倾斜
//4 整型 旋转后的所有虚线改为实线 并向右倾斜

//树和森林没有 中序遍历

//赫夫曼树  最优树 带权路径最短的树
//树的路径长度  树根到每个节点的路径长度之和
//带权的路径长度 从该节点到树的根节点之间的路径长度与节点的权的乘积

2 Huffman树

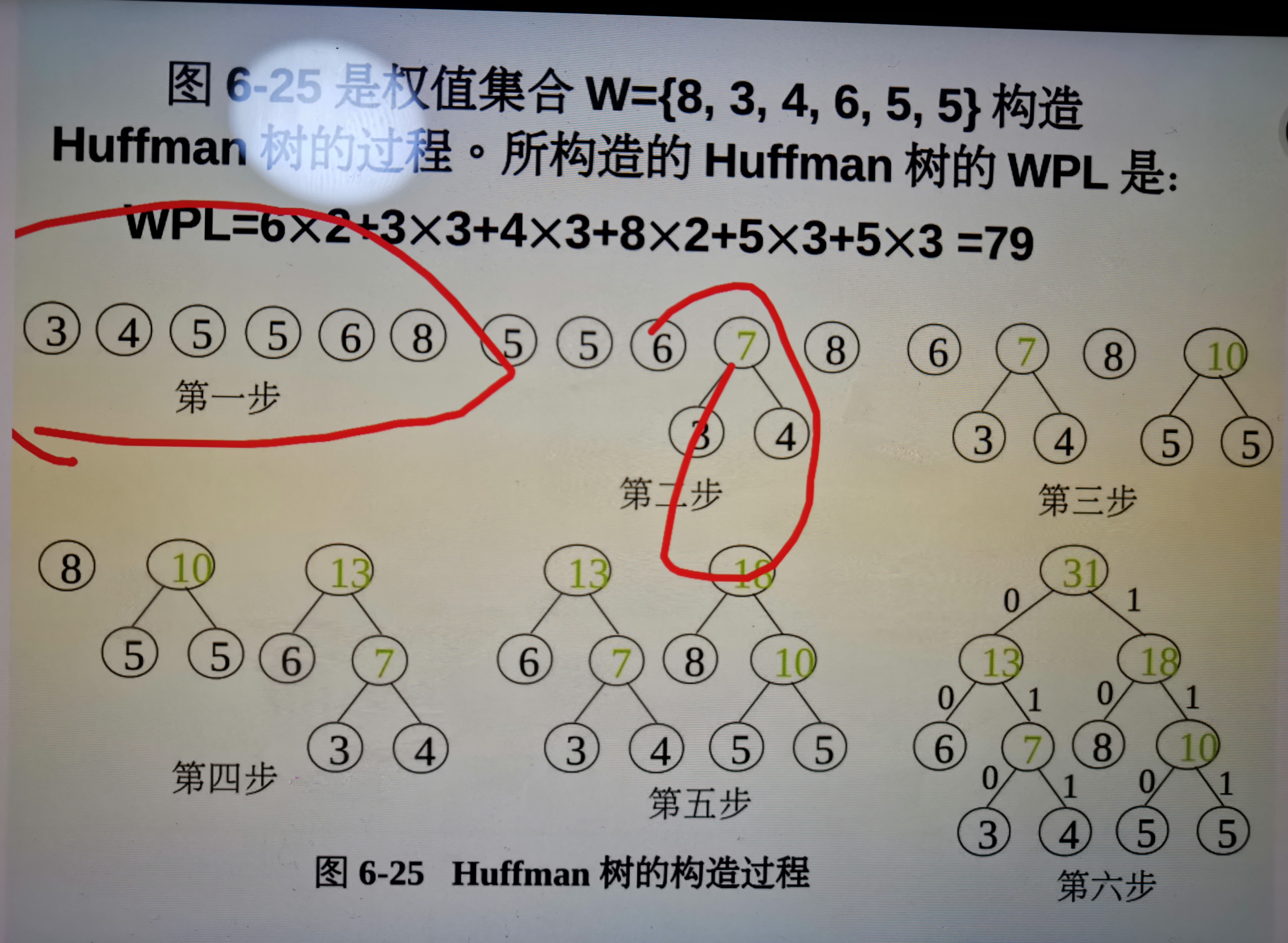
typedef struct
{
    unsigned int Weight;
    unsigned int Parent, Lchild, Rchild;
}HTNode;
//创建一颗叶子节点数为n的Huffman数
//生成Huffman数后 树的根节点的下标是2n-1 即m-1
void Create_Huffman(unsigned n, HTNode HT[], unsigned m)
{
    unsigned int w; int k, j;
    for (k = 1; k < m; k++)
    {
        if (k <= n)
        {
            cout << "Please Input Weighrt:w=?" << endl;
            cin >> w; HT[k].Weight = w;
        }
        else HT[k].Weight = 0;
        HT[k].Parent = HT[k].Lchild = HT[k].Rchild = 0;
    }
    for (k = n + 1; k < m; k++)
    {
        unsigned w1 = 32767, w2 = w1;  //分别保存权值最小的两个
        int p1 = 0, p2 = 0;   //分别保存最小权值的下标
        for (j = 1; j <= k - 1; j++)
        {
            if (HT[k].Parent == 0)  //尚未合并
            {
                if (HT[j].Weight < w1)
                {
                    w2 = w1; p2 = p1;
                    w1 = HT[j].Weight; p1 = j;
                }
                else if(HT[k].Weight<w2)
                {
                    w2 = HT[j].Weight; p2 = j;
                }
            }
        }
        HT[k].Lchild = p1; HT[k].Rchild = p2;
        HT[k].Weight = w1 + w2;
        HT[p1].Parent = k; HT[p2].Parent = k;
    }
}

3 Huffman编码

　　Huffman可以用来构造编码长度不等且译码不产生二义性的编码。

　　我们对生成的Huffman树，进行编码。

　　产生的编码如下：

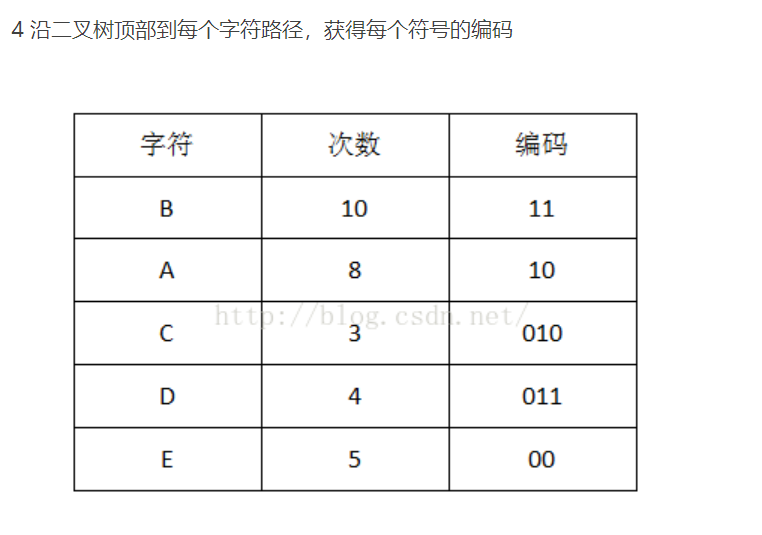
　　Huffman编码算法，又来那种处理的方式：

1 从叶子节点到根节点逆向处理，求得每个叶子节点的对应字符的Huffman编码。

2 从根节点开始遍历整个二叉树，求得每个叶子节点得对应字符得Huffman编码。

//Huffman编码算法
//根据出现频度（权值）weight，对叶子节点的Huffman编码。
void Huff_coding(unsigned n, Hnode HT[], unsigned m)
{
    int k, sp, fp;
    char* cd, * HC[m];
    cd = (char*)malloc(m * sizeof(char));
    cd[n] = '\0';
    for (k = 1; k < n + 1; k++)
    {
        sp = n; p = k; fp = HT[k].parent;
        for (; fp != 0; p = fp, fp = HT[p].parent)
            if (HT[fp].Lchild == p)cd[--sp] = '0';
            else cd[--sp] = '1';
        HC[k] = (char*)malloc((n - sp) * sizeof(char));// 为第k个字符分配保存编码二定空间
        strcpy(HC[k], &cd[sp]);
    }
    free(cd);
}

　　上述代码为第一种。产生得编码在HC多维数组保存。