【学习笔记】图论建模

开个坑，之前写过的就算了以后碰见再加。

差分约束

考虑一组变量 \(x_1,x_2,\cdots,x_n\)，现在我们有若干不等关系形如 \(x_1-x_2\le t\)，求一组合法的解。

发现 \(x_1-x_2\le t\) 形似最短路中 \(dis_x-dis_y\le w(x,y)\)，把这张图建出来跑最短路即为一组合法解。若出现负环代表原不等式组无解。由于最短路的优美性质，差分约束系统得到的一组解是在下界上字典序最小的解。

常见的转化：

• \(x_1-x_2\ge t\to x_2-x_1\le -t\)。

• \(x_1=x_2\to x_1-x_2\le0,x_1-x_2\ge0\)。

• \(\frac{x_1}{x_2}\le t\to\log x_1-\log x_2\le\log t\)。

加点可以视作减去该点负点权，但此时回溯得到的解不满足字典序最小的性质。

网络流

拆点

比较经典的建模方法，如果一个点无法表示所有信息就把这一个点拆成多个点。用的时候需要思考拆出来的点之间有何关系，该是否需要以及如何表示拆出来的这些点原来是一个点。

P3153

经典地将每个男/女拆成两点分别表示与喜欢的对象连边和与不喜欢的对象连边。对于喜欢的部分其容量为 \(\infty\)，对于不喜欢的部分其容量为 \(k\)。

P2764 最小路径覆盖

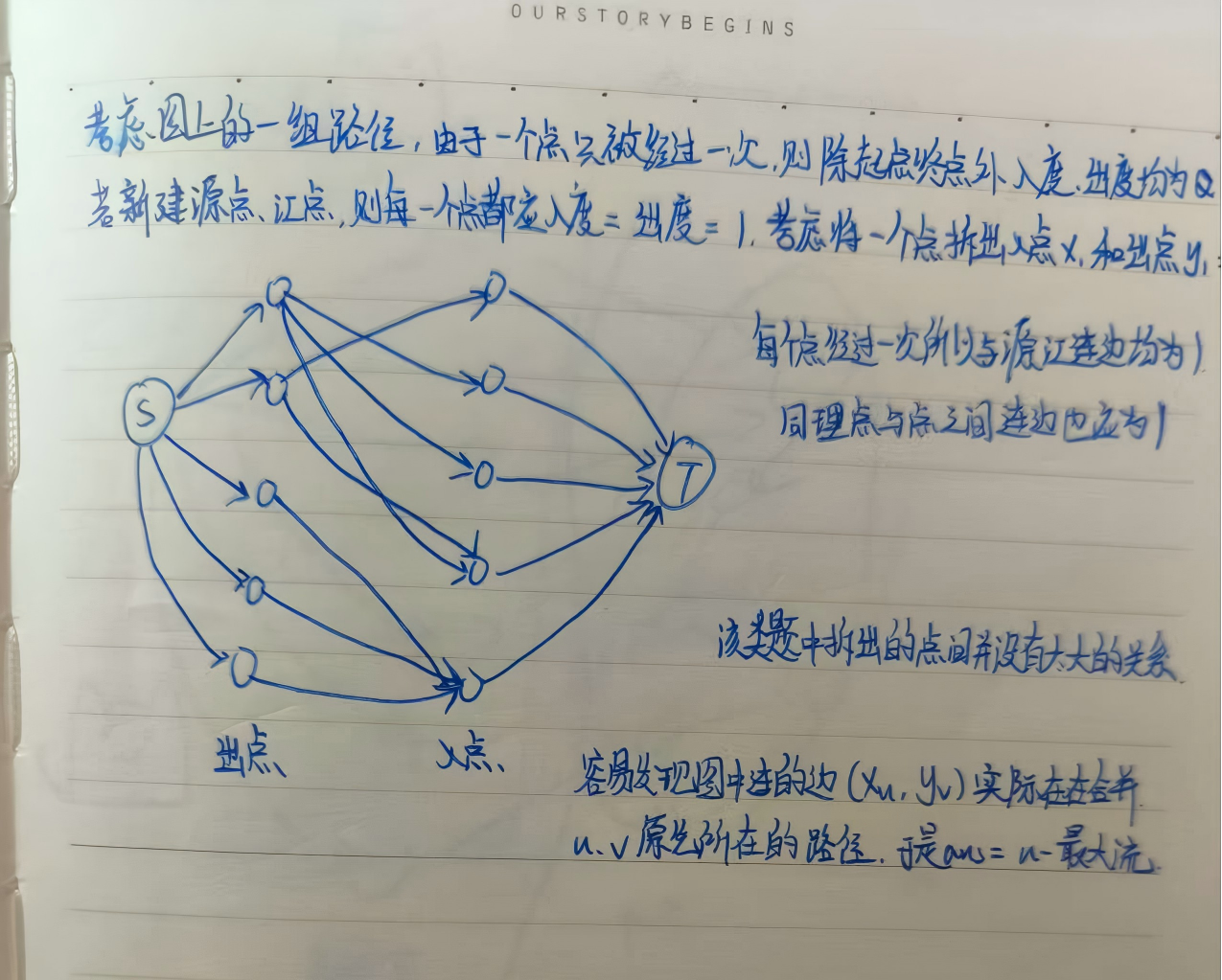
二分图最大权独立集

给一张二分图，点有点权，问最大权独立集。普通图最大权独立集是不可做的，所以一定要二分图才有性质。

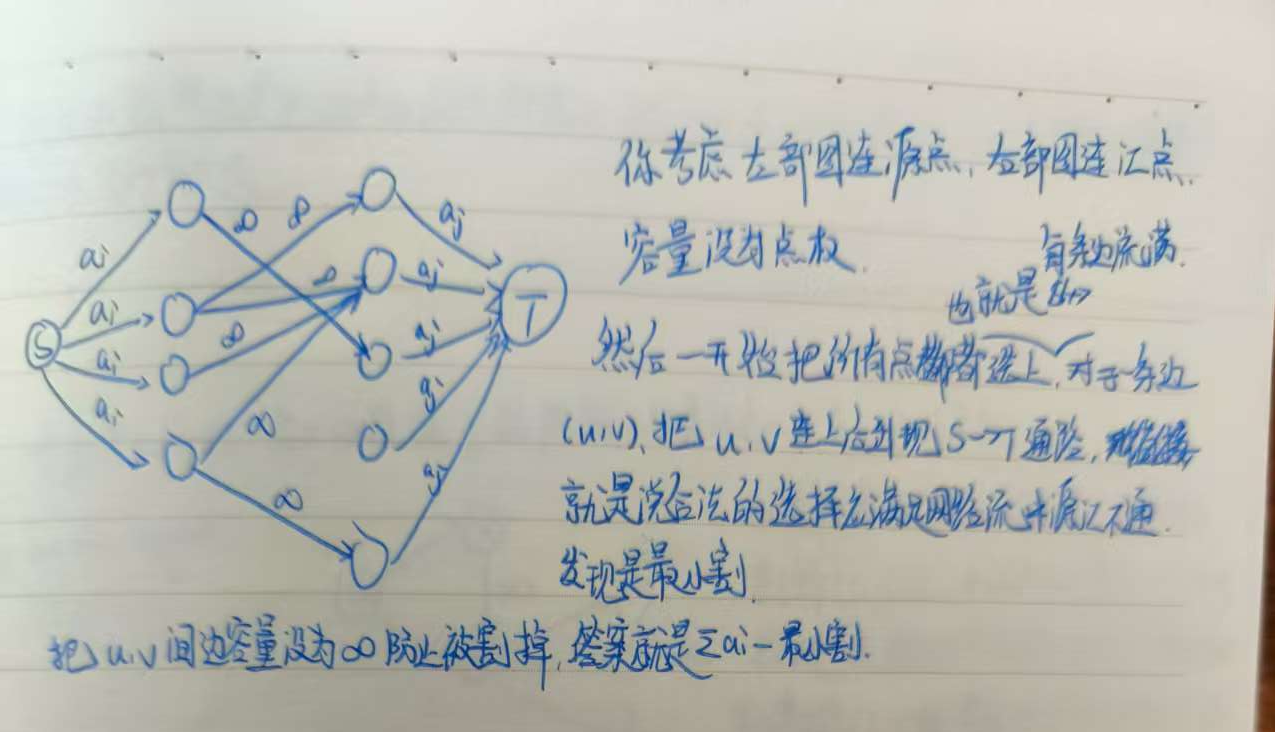
最大权闭合子图

给一个图，点有点权，一条有向边 \(x\to y\) 表示若选择 \(x\) 必须选择 \(y\)，求满足该条件下最大点权和。

最直观的想法就是把正点权的点全部选上。选与不选是将图划分为两个集合的题目，考虑最小割。

所以对于 \(a_i>0\) 的 \(i\) 连边 \(S,i,a_i\)，割掉这条边代表不选择点 \(i\)，失去 \(a_i\) 的代价。对于 \(a_i<0\) 的 \(i\) 连边 \(i,T,-a_i\)，割掉这条边代表选择点 \(i\)，失去 \(-a_i\) 的代价。

此类选择的限制具有传递性，很好地帮助我们简化了建图的情况数。

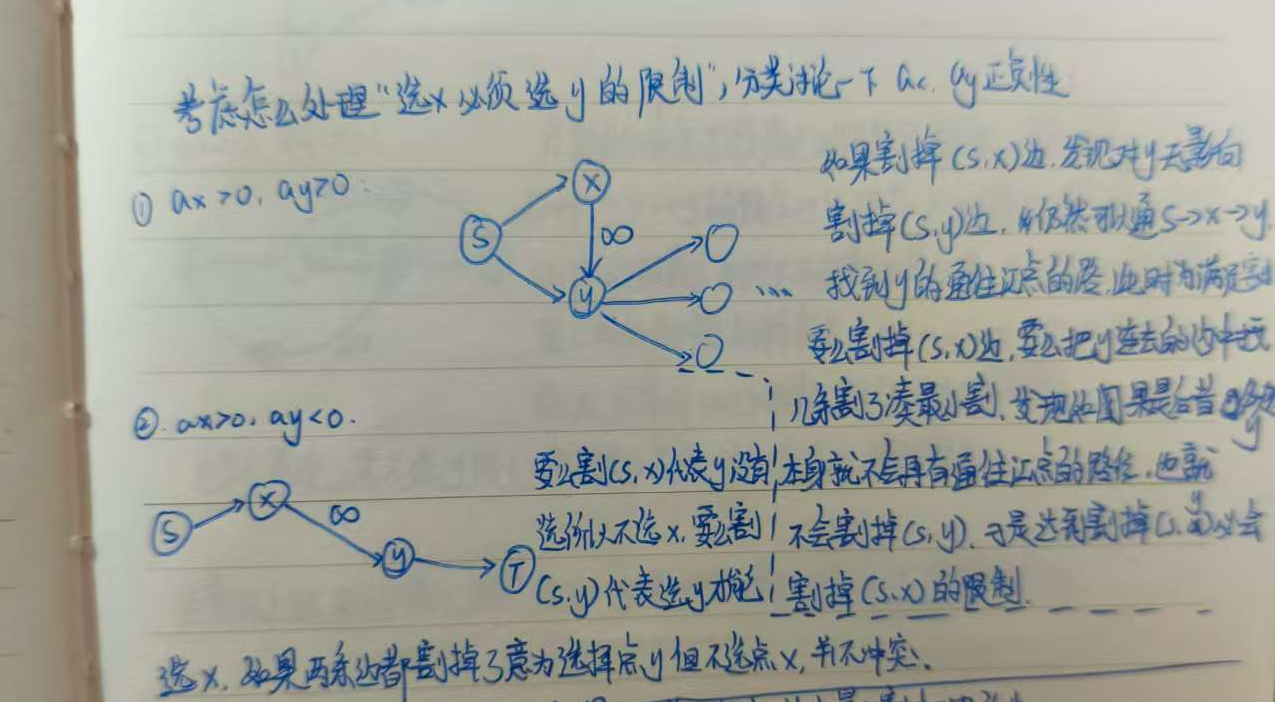
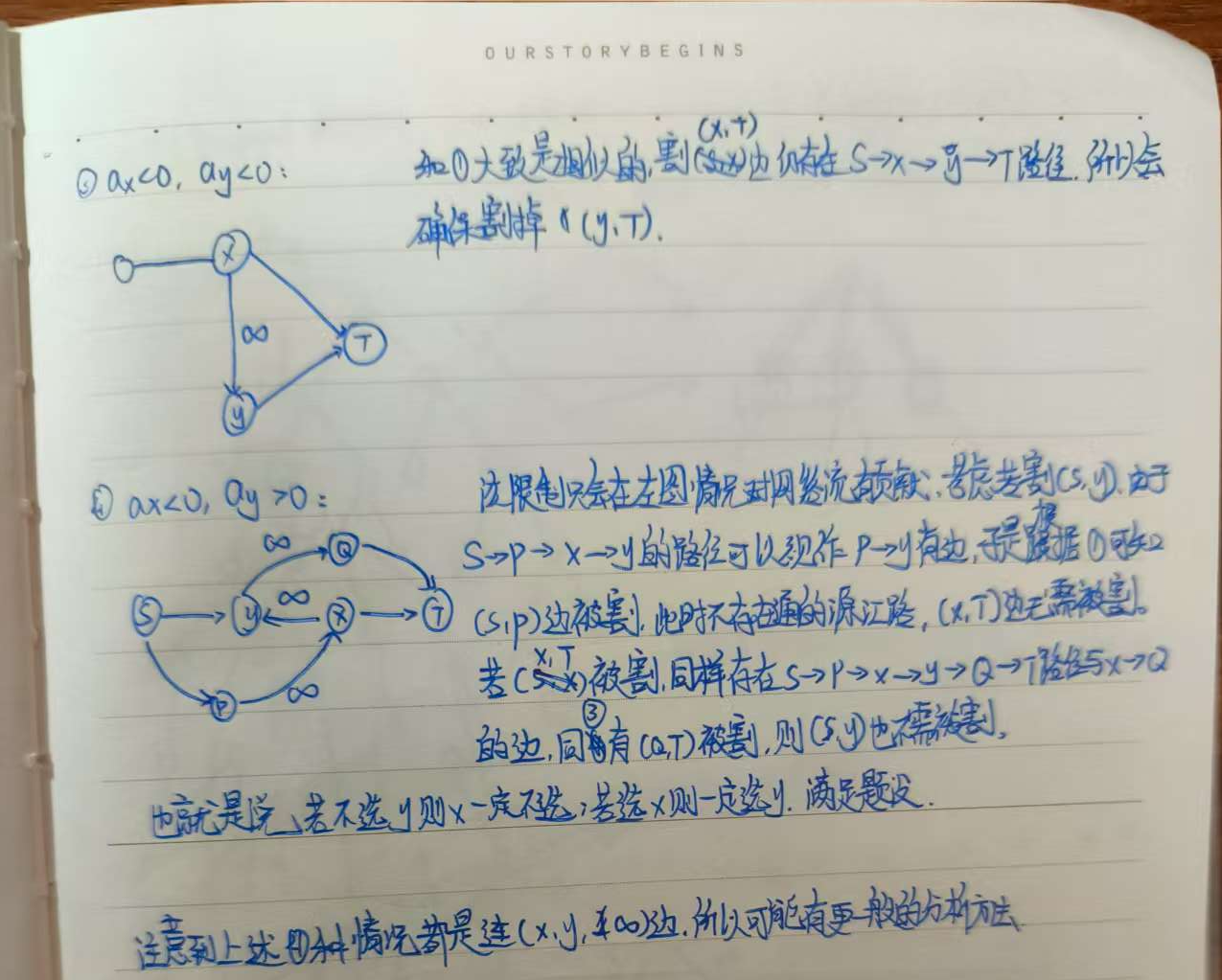
距离模型

咕咕咕。

二元关系

同时选择 \(x\) 与 \(y\) 可能得到新的代价。如果不知道如何建边权，为什么不把有关系的边全部建出来解方程呢？

P1646

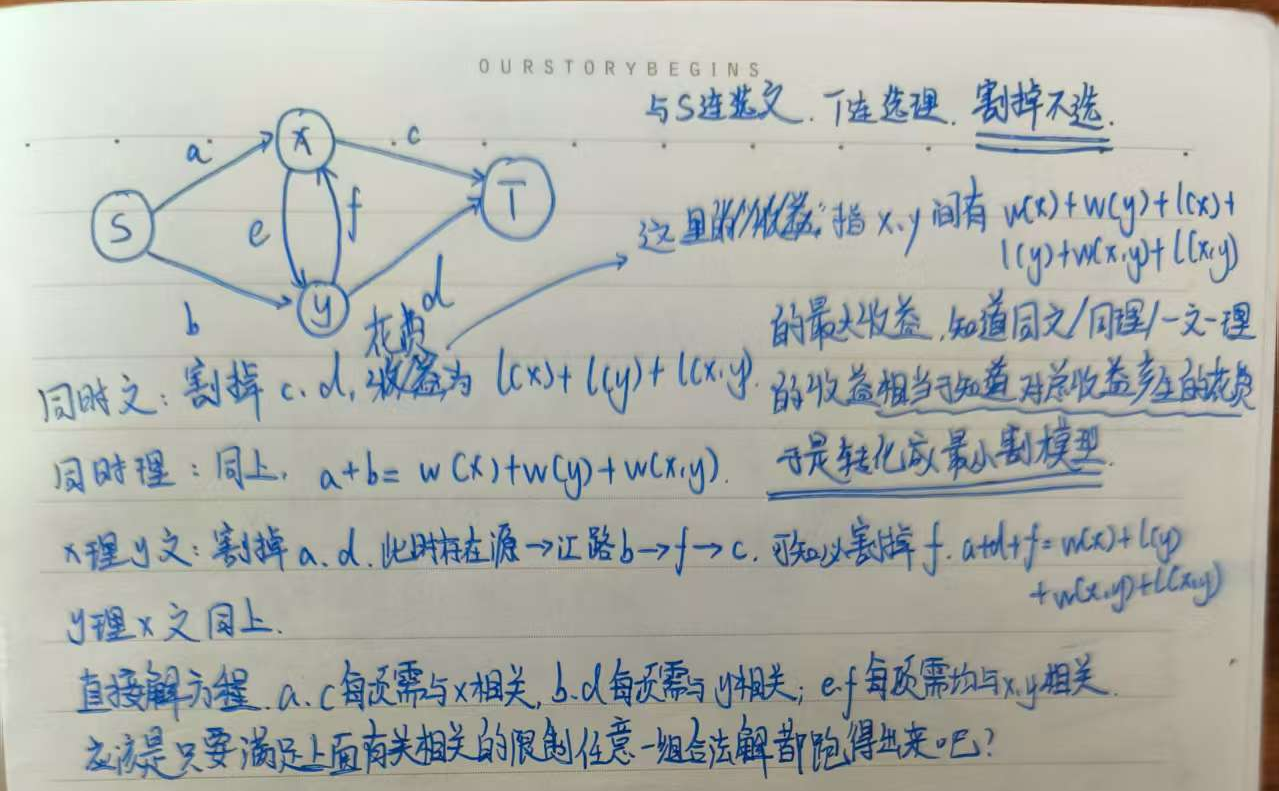
度数限制

还不会咕咕咕。

区间覆盖

考虑如下的一种问题：有几个区间 \([l_i,r_i]\)，每个区间有权值 \(a_i\)，选择一些区间使得在每个点被覆盖次数 \(\le k\) 的限制下选择的区间权值最大。