背包六讲(也不知道为啥就是六个 $QwQ$)
浅谈
对于本文来说,如果没有特殊声明,则题目描述的顺序就是输入的顺序,题目来源皆来自于AcWing;
本文为了压缩文本,题目只给大意,寻找数据,还请到AcWing寻找。
明确些东西
\(1.\)容量 : 也就是这一个题中 , 我们怎样表示状态的数组
\(2.\)体积(费用) : 也就是这一个题中 , 我们用来转移的数组,或者说,建立关系的数组
\(3.\)价值 : 也就是我们维护的数组。
1. 01背包
【题目描述】:有\(N\)件物品和一个容量是\(V\)的背包。每件物品只能使用一次。第\(i\)件物品的体积是\(v_i\),价值是\(w_i\)。求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值。
\(f_{i,j}\)表示总共拿第\(i\)种物品,总共花费\(j\)体积的最大价值
第一层循环枚举每一个物品,看一下是否可以拿第\(i\)种物品,同时,第二层循环,枚举体积\(j\);
【状态转移】:
当前背包的体积不够这个物品放的(\(j<v_i\)),前\(i-1\)个物品最优解 \(f_{i,j}=f_{i-1,j}\)
当前背包的体积够的时候,面临两个选择:
选的时候:\(f_{i,j} =max(f_{i,j},f_{i-1,j-v_i+}w_i)\)
不选的时候: \(f_{i,j}=f_{i-1,j}\)
然后就开始了:
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
int n,m;
int w[1001],v[1001];
int f[1001][1001];
int main()
{
scanf("%d%d",&n,&m);
for(register int i=1;i<=n;i++)
{
scanf("%d%d",&v[i],&w[i]);
}
for(register int i=1;i<=n;i++)
{
for(register int j=0;j<=m;j++)
{
f[i][j]=f[i-1][j];//这个初始化的意思就是,我们不选这个物体
if(j>=v[i])
{
f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+w[i]);//状态转移
}
}
}
cout<<f[n][m]<<endl;
return 0;
}
然后发现这个是恶心的两维,然后复杂度是O(\(nm\)),接下来我们考虑一下优化(滚动数组不会)
-
优化(二维压成一维的可行性)
f_{i,j}=f_{i-1,j}$ (不含i的所有的选法的最大价值)
\(f_{i,j}=max(f_{i,j},f_{i-1,j-v_i}+w_i)\) (包含物品i的所有选法的最大价值)
然后发现,第\(i\)物品的状态取决于第\(i-1\)件物品的状态,那么我们就没必要保留第\(i-2\)的物品的状态了(具体问题具体说,这里是板子) -
对于优化后的01背包为什么需要倒序枚举,一开始我也确实是很迷,在 \(nyx\)的帮助下理解了一下,经过 11.18号的学习,之后,也是明白了,说一下:
优化完之后我们只有上一层的状态,更新值的时候也是只能原地滚动更改,我们在更新索引值较大的dp值的时候需要索引值较小的,也就是需要保证在更
新索引值较大的dp值之前,必须保证索引值较小的上一层的dp值还在,且没被更新,所以我们需要从大到小枚举,换个意思说,如果我们从小到大枚举,
我们现在更新体积为\(j\)的情况,我们需要用到\(j-v_i\)的,我们需要记录同时我们进行更改,而到了其他的体积\(j_2\),状态转移的时候需要前面的体积,会重新覆盖导致错误。
然后代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
int f[1001],n,m;
int v[1001];
int w[1001];
int main()
{
scanf("%d%d",&n,&m);
for(register int i=1;i<=n;i++)
{
scanf("%d%d",&v[i],&w[i]);
}
for(register int i=1;i<=n;i++)
{
for(register int j=m;j>=v[i];j--)
{
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
cout<<f[m]<<endl;
return 0;
}
2. 完全背包:
【题目描述】:有\(N\)种物品和一个容量是\(V\)的背包,每种物品都有无限件可用。第\(i\)种物品的体积是&v_i&,价值是\(w_i\)。求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值。
【解题思路】:
第一层循环枚举物品的种类\(i\),第二层循环枚举体积\(j\),第三次循环则是枚举不大于体积\(j\)的最大的物品个数,
状态转移方程:看一下 01 背包,也就十分清楚了
\(f_{i,j}=max(f_{i,j},f_{i-1,j-k*v_i}+k*w_i)\)
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cmath>
using namespace std;
int n,m;
int v[1001],w[1001];
int f[1001][1001];
int main()
{
scanf("%d%d",&n,&m);
for(register int i=1;i<=n;i++)
{
scanf("%d%d",&v[i],&w[i]);
}
for(register int i=1;i<=n;i++)
{
for(register int j=0;j<=m;j++)
{
for(register int k=0;k*v[i]<=j;k++)
{
f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
}
}
}
cout<<f[n][m]<<endl;
return 0;
}
然后发现这个复杂度挺高的,O(\(nm^2\)),很容易就会\(TLE\)掉,所以类比于01背包,然后就容易优化了
状态转移方程
\(f_j=max(f_j,f_{j-v_i}+w_i)\)
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
int n,m;
int v[1001],w[1001];
int f[1001];
int main()
{
scanf("%d%d",&n,&m);
for(register int i=1;i<=n;i++)
{
scanf("%d%d",&v[i],&w[i]);
}
for(register int i=1;i<=n;i++)
{
for(register int j=v[i];j<=m;j++)//01背包从大到小。完全背包从小到大
{
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
cout<<f[m]<<endl;
return 0;
}
同样的,我还是不会滚动数组,所以也就是优化到这了
3.多重背包
【题目描述】:
有\(N\)种物品和一个容量是\(V\)的背包。第\(i\)种物品最多有\(s_i\)件,每件体积是\(v_i\),价值是\(w_i\)。求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。输出最大价值。
【思路分析】:
对于这个题来说,我们可以直接将这个多重背包拆开,拆成\(01\)背包,可以理解到那个场面,无非也是多了一层循环,其余均一样,去掉第一维的优化过程也就没必要说了,值得一说的是多重背包的两种大优化(能过20000的),
【Code】:类比01背包优化(非优化):
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <set>
using namespace std;
const int maxn=1e6;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int n,m;
int s[maxn],v[maxn],w[maxn];
int f[maxn];
int main()
{
n=read(),m=read();
for(int i=1;i<=n;i++)
{
v[i]=read(),w[i]=read(),s[i]=read();
}
for(int i=1;i<=n;i++)
{
for(int j=m;j>=0;j--)
{
for(int k=0;k<=s[i];k++)
{
if(j>=k*v[i])
{
f[j]=max(f[j],f[j-k*v[i]]+k*w[i]);
}
}
}
}
printf("%d",f[m]);
return 0;
}
【优化方案,二进制优化】:
我们十分容易发现,我们在没有优化的时候是把多重背包全部拆分成\(01\)背包,但如果数据大了, 光拆分时间复杂度就已经够了。
再接下来我们想起来,如果我们不是一个个的拆分成\(01\)背包,而是拆分成一堆一堆的呢,利用二进制的思想进行拆分,在拆分的时候我们直接选择一堆一堆的,就例如,我们选3个物品\(A\),最优,如果是\(01\)背包的话,就是分成 1 ,1, 1;但是如果二进制优化了,就是 1 , 2,数据更大,则优化的更加明显,总而言之就是,拆分成二的倍数(如果拆到不能拆的时候,就是自己一个背包就可以了) 1,2,4,8,12,24,48,……之类的,反正就是可以凑出需要的背包数,就比如 11个物品\(A\),11在二进制下,是\(1011=1000+10+1\) 然后 \(1000=4,10=2,1=1\),只需要 物品个数为1,2,4的三堆就可以了。
/*二进制优化多重背包*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <set>
#include <vector>
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
struct Node
{ //定义结构体用它重新构建01背包
int volume;
int value;
};
int f[2000],n,m;
int main()
{
vector<Node>Goods; //定义结构体数组
cin>>n>>m; //输入物品数和背包大小
for(int i=1;i<=n;i++)
{
int volume,value,counts;
cin>>volume>>value>>counts;//现场输入物品的体积、价值、数量
for(int j=1;j<=counts;j<<=1)//开始拆解数量重新构建商品赋予价值和体积
{
counts-=j;
Goods.push_back({j*volume,j*value});
}
if(counts>0) //如果有剩余单独构建一个商品
{
Goods.push_back({counts*volume,counts*value});
}
}
for(int i=0;i<Goods.size();i++)//接下来就是熟悉的01背包了遍历每件商品
{
for(int j=m;j>=Goods[i].volume;j--)//体积从大到小
{
f[j]=max(f[j],f[j-Goods[i].volume]+Goods[i].value);//状态转移
}
}
cout<<f[m]<<endl;//输出答案
return 0;
}
再优化,单调队列优化:请见 单调队列第三个
4.分组背包
【题目描述】:
有\(N\)组物品和一个容量是\(V\)的背包。每组物品有若干个,同一组内的物品最多只能选一个。每件物品的体积是\(v_{i,j}\),价值是\(w_{i,j}\),其中\(i\)是组号,\(j\)是组内编号。求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。输出最大价值。
【思路分析】:
每一个分组都可以看成一个集合\(A\),那么我们只能从这里面挑出一个物品\(k\),也就是\(k \in A\),所以可以在\(k\)和集合\(A\)中建立关系,可能会想到建图,但是当\(A\)中的编号为\(k\)的物品已经\(OK\)了,我们的状态转移也应该用到这个\(k\)要还是不要决定下一个,这样的话,你的写一个很难表示,所以直接用一个二维数组来表示就可以了。然后就可以开始了;
【状态设计】:
还是 \(f_{i,j}\)表示从前\(i\)组选,体积为\(j\)的最大价值
【状态转移】:
我们考虑,在 \(f_{i,j}\)可以由什么得到,它可以由同一组的得到,也可以从上一组的得到,那么状态转移的时候外层循环就需要枚举总共有多少组了(同时也就是说,我们也应该求出组数,例如link,就别忘了求),
\(f_{i,j}=max(f_{i-1,j}, \max\limits_{0\leq k\leq该组的所有物品数} f_{i-1,j - v_{i,k}}+w_{i,k})\)表示从前\(i\)组选,但是我们有两个选择就是可以不选该该组中的物品或不选
选,那么就是 \(f_{i-1,j}\);
不选对应的情况就是\(\max\limits_{0\leq k\leq该组的所有物品数} f_{i-1,j - v_{i,k}}+w_{i,k}\)其中 \(v_{i,k}\)表示的是在第\(i\)组中的第\(k\)个物品所应对的体积,那么自然,\(w_{i,k}\)表示的就是价值了。
【代码】:
#include<iostream>
#include<algorithm>
using namespace std;
const int N=110;
int f[N][N],v[N][N],w[N][N],s[N];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>s[i];
for(int j=1;j<=s[i];j++)//第 i组背包的第 j个物品体积,价值
{
cin>>v[i][j]>>w[i][j];
}
}
for(int i=1;i<=n;i++)//n组,背包,枚举背包数目
{
for(int j=0;j<=m;j++) // 枚举体积 ,类比前面的背包
{
f[i][j]=f[i-1][j];
for(int k=1;k<=s[i];k++)//枚举每一组中的物品
{
if(j>=v[i][k]) //体积够才拿,不然你拿个锤子
{
f[i][j]=max(f[i][j],f[i-1][j-v[i][k]]+w[i][k]);
}
}
}
}
cout<<f[n][m];
return 0;
}
类比01背包优化一下,去掉第一维:
【Code】:(上一个有注释,这个就不要了吧\(QwQ\))
#include<iostream>
#include<algorithm>
using namespace std;
const int N=110;
int f[N],v[N][N],w[N][N],s[N];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>s[i];
for(int j=1;j<=s[i];j++)
{
cin>>v[i][j]>>w[i][j];
}
}
for(int i=1;i<=n;i++)
{
for(int j=m;j>=0;j--)
{
for(int k=1;k<=s[i];k++)
{
if(v[i][k]<=j)
{
f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
}
}
}
}
cout<<f[m];
return 0;
}
【注意】:
1.倒序枚举 \(j\) 类比01背包的优化
2.对于每一组内 \(s_i\)个物品的循环\(k\)应放在\(j\)的内层。从背包角度看,这是因为每组内至多选一个物品,若把\(k\)置于\(j\)的外层,就会类似于多重背包。每组背包在\(f\)数组上转移就会产生累积,最终可以选择超过1个物品。从动态规划角度看,\(i\)是阶段,\(i\)和\(j\)共同组成“状态”,而\(k\)是决策——在第i组内使用哪一个物品。这三者的顺序绝对不能混淆。 ————李煜东《算法竞赛进阶指南》
5.有依赖性的背包
【题目分析】:
有 N 个物品和一个容量是 V 的背包。物品之间具有依赖关系,且依赖关系组成一棵树的形状。如果选择一个物品,则必须选择它的父节点。如下图所示:
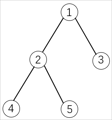
如果选择物品5,则必须选择物品1和2。这是因为2是5的父节点,1是2的父节点。每件物品的编号是\(i\),体积是\(v_i\),价值是\(w_i\),依赖的父节点编号是\(p_i\)。物品的下标范围是 1…N。求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。输出最大价值。
【输入格式】
第一行有两个整数 N,V,用空格隔开,分别表示物品个数和背包容量。
接下来有 N 行数据,每行数据表示一个物品。
第\(i\)行有三个整数\(v_i,w_i,p_i\)用空格隔开,分别表示物品的体积、价值和依赖的物品编号。
如果 \(p_i\)=−1,表示根节点。 数据保证所有物品构成一棵树。
【输出格式】:
输出一个整数,表示最大价值。
【思路分析】:
很明显,所属关系是一棵树,那么我们要建树,同时考虑一下该节点的信息从何而来,树形DP的状态往往来自于子节点或者父亲节点。发现我们在分配背包空间时,不再像之前一样按每一个物品分配背包空间,发现,根节点必须选(你不选你啥都没有),然后根节点就可以分配到全部的背包空间,然后根节点的儿子节点记为\(to\),则\(\sum v_{to}=分配的空间-v_{根节点}\),也就是说,他的儿子节点和他自己共同分享这个背包的空间,所以我们在状态转移的时候也就是要直接转移空间的大小,而不是枚举物品数目(儿子还有儿子,儿子的儿子还有儿子,子子孙孙无穷匮也),但是我们只要一遍Dfs(大风扇),就可以初始化选择这个点的全部价值,最后在回溯的时候就考虑\(now\)和它的儿子结点的转移即可。
【状态设计】:
我们搞清楚是怎么分配的体积就可,方式就是按每一个子树分多少体积进行分组,每棵子树对应一组,所以状态也就是 \(f_{i,j}\)表示的是节点i为子树分配\(j\)体积的最大价值,其中\(i\)为子树,等价于分组背包中的一组,结合上文yy一下;
【状态转移】:
\(f_{now,j}=\max\limits_{0 \leq k \leq j-v_{now}}(f_{now,j},f_{now,j-k}+f_{to,k})\)表示now这颗子树,中分配\(j\)体积的最大值就是只选择这颗子树的根,或者就是选择这颗子树的某些节点,但是这些节点也不一定全选(全选还DP个锤子),给节点分大小为\(k\)的体积,\(DP\)一下,然后看一下最大值就行了,
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int maxn=1e6;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
struct node
{
int nxt,to;
}edge[maxn<<1];
int n,m,number_edge,root;
int v[maxn],w[maxn],head[maxn];
void add_edge(int from,int to)//建树自然要用到邻接表,啊这,我不会vector
{
number_edge++;
edge[number_edge].nxt=head[from];
edge[number_edge].to=to;
head[from]=number_edge;
}
int f[1001][1001];//上面的状态设计就不必说了
void dfs(int now,int fa)//英文缩写简洁明了
{
for(int i=v[now];i<=m;i++)//既然到了 now这个点,那么就意味着,必须选这个点了,所以初始化
{
f[now][i]=w[now];
}
for(int i=head[now];i;i=edge[i].nxt)
{
int to=edge[i].to;
if(to==fa)//不能嗨皮地回去
{
continue;
}
dfs(to,now);
//合并
for(int j=m;j>=v[now];j--)// j的范围就是 m 到 v[now],如果小于,那么也就是不能选择 now这棵子树上的
{
for(int k=0;k<=j-v[now];k++)//采取分空间,直接分给子树k的空间树
{
f[now][j]=max(f[now][j],f[now][j-k]+f[to][k]);
}
}
}
}
int main()
{
n=read(),m=read();
for(int i=1;i<=n;i++)
{
int fa;
v[i]=read(),w[i]=read(),fa=read();
if(fa==-1)//求出根节点
{
root=i;
}
else //建立树边
{
add_edge(i,fa);
add_edge(fa,i);
}
}
dfs(root,0);//开始树形DP
printf("%d",f[root][m]);//ans,如果树上的一个节点存储多个信息,那么ans就不这么简单了
return 0;
}
6.二维费用背包:
【题目描述】:
有\(N\)件物品和一个容量是\(V\)的背包,背包能承受的最大重量是\(M\)。每件物品只能用一次。体积是\(v_i\),重量是\(m_i\),价值是\(w_i\)。求解将哪些物品装入背包,可使物品总体积不超过背包容量,总重量不超过背包可承受的最大重量,且价值总和最大。输出最大价值。
【思路分析】:
有点显而易见了,不再局限于体积,还要有价值,无非就是多了一层循环罢了
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int maxn=1e3;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int n,m,s;
int f[maxn][500][500],w[maxn],v[maxn],l[maxn];
int main()
{
n=read(),m=read(),s=read();
for(int i=1;i<=n;i++)
{
v[i]=read(),l[i]=read(),w[i]=read();
}
for(int i=1;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
for(int k=0;k<=s;k++)
{
f[i][j][k]=f[i-1][j][k];//不拿
if(k>=l[i] && j>=v[i])//先判断一下是否能拿,这个地方不能把这个判断放到循环里面
{
f[i][j][k]=max(f[i-1][j-v[i]][k-l[i]]+w[i],f[i][j][k]);
}
}
}
}
printf("%d",f[n][m][s]);
return 0;
}
再次优化后
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
using namespace std;
int n,m,v;
int f[1001][1001];
int mi[1001],vi[1001],wi[1001];
int main()
{
scanf("%d%d%d",&n,&v,&m);
for(register int i=1;i<=n;i++)
{
scanf("%d%d%d",&vi[i],&mi[i],&wi[i]);
}
for(register int i=1;i<=n;i++)
{
for(int j=v;j>=vi[i];j--)
{
for(int k=m;k>=mi[i];k--)
{
f[j][k]=max(f[j][k],f[j-vi[i]][k-mi[i]]+wi[i]);
}
}
}
cout<<f[v][m]<<endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号