# [NOIP 2016 提高组] 天天爱跑步 题解

简要题意

给定一个拥有 \(n\) 个节点的树和 \(m\) 条运动路径，求对于每个点 \(u\) , 在 \(w_i\) 时刻经过此点的玩家数量。

思路

暴力

首先暴力模拟每个玩家的运动路径来计算对每个节点 \(u\) 是否有贡献是不可取的，最劣时（即树退化成链）复杂度为 \(\Theta(nm)\) 。

转化

于是我们可以转换思路，不枚举玩家对每个节点 \(u\) 的贡献。那我们还能枚举什么呢？ 显而易见，我们只剩下枚举每个点 \(u\) 看哪些玩家对他有贡献了，处理贡献时只需要 dfs 一遍这个树就可以了。

问题就转化成我们怎样才能计算出和统计贡献， 因为每个玩家的的运动速度是一定的，所以到达每个点的时间可以直接转化成距离，而树上的距离往往和深度又会有关系，于是我们又将距离转化到了深度之间的关系。

分类讨论

对于节点 \(p\) ，当他在一条起点在 \(s\)， 终点在 \(t\) 的路径上时，怎么判断玩家有没有对它做贡献呢？

显而易见的，有两种情况

在 \(s\) 到 \(\text{LCA}(s, t)\) 上

如图所示：

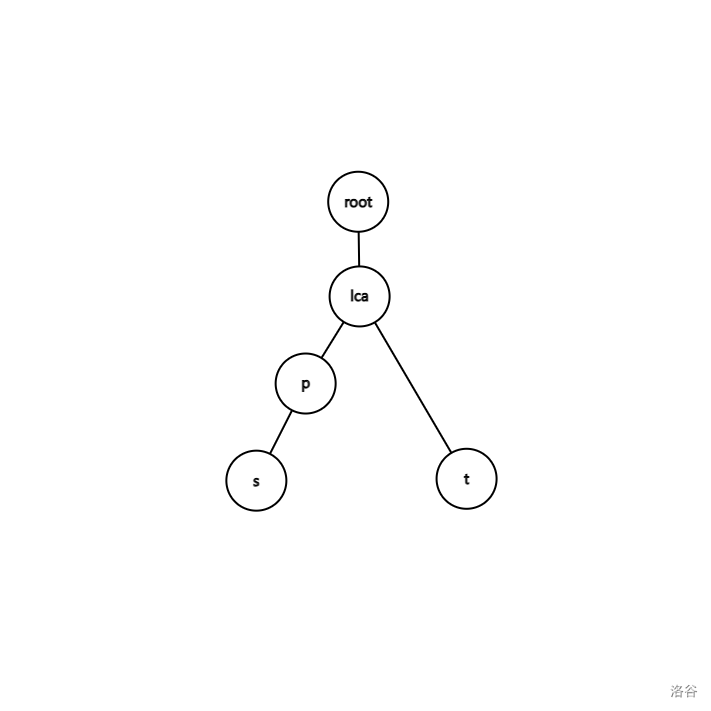
那么符合条件的 \(p\) 一定满足： \(\text{dist}(s,p) = w_p = dep_s - dep_p\) ，由于 \(s\) 是固定的，所以我们进行移项，得 \(w_p + dep_p = dep_s\)

所以当 \(w_p + dep_p = dep_s\)时， \(s\) 会对 \(p\) 做一个贡献。

在 \(t\) 到 \(\text{LCA}(s, t)\) 上

如图：

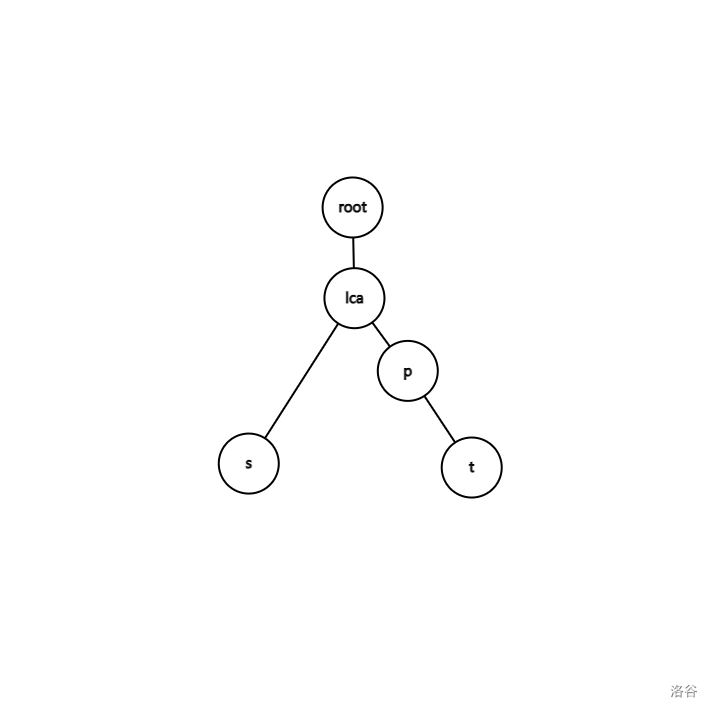
同理，符合条件的 \(p\) 满足：\(\text{dist}(s,p) = w_p = dep_s + dep_p - 2 \times dep_{lca}\) ，仿照上文移项得 $w_p - dep_p + 2 \times dep_{lca}= dep_s $

如何统计

我们对每个节点开两个单点修改单点查询的动态开点权值线段树（貌似有点鸡肋），利用树上差分分别统计两种情况的贡献，最后查询递归时进行线段树合并后单点查询就行了。

对于第一种情况，\(p\) 的贡献来自于路径 \(s \to lca\) 所以在 \(s\) 处增加 \(dep_s\) 的贡献，再在 \(lca\) 的父亲处减少贡献。第二种情况类似。

查询时，对于每个点 \(p\) ，第一种情况直接查询 \(w_p + dep_p\) 的点有多少个，第二种类似。

Code:

#include <bits/stdc++.h>
//#define int long long
using namespace std;
int n, m;
/*链式前向星*/
constexpr int MAXN = 3e5 +5;
struct ed {
	int to, nxt;
} edge[MAXN << 1];
int head[MAXN];
int tot;
void add_edge(int u, int v) {
	edge[++tot].to = v, edge[tot].nxt = head[u], head[u] = tot;
}
/*倍增求LCA*/
constexpr int LOG = 20;
int dep[MAXN], dp[MAXN][LOG];
void dfs(int u, int fa) {
	dep[u] = dep[fa] + 1, dp[u][0] = fa;
	for (int i = head[u]; ~i; i = edge[i].nxt) {
		int v = edge[i].to;
		if (v == fa)
			continue;
		dfs(v, u);
	}
}
void init() {
	dfs(1, 0);
	for (int j = 1; j < LOG; ++j)
		for (int i = 1; i <= n; ++i)
			dp[i][j] = dp[dp[i][j - 1]][j - 1];
}
int lca(int u, int v) {
	if (dep[u] < dep[v])
		swap(u, v);
	if (dep[u] != dep[v]) {
		for (int i = LOG - 1; i >= 0; --i)
			if (dep[dp[u][i]] >= dep[v])
				u = dp[u][i];
	}
	if (u == v)
		return u;
	for (int i = LOG - 1; i >= 0; --i)
		if (dp[u][i] != dp[v][i])
			u = dp[u][i], v = dp[v][i];
	return dp[u][0];
}
/*动态开点权值线段树*/
class SegmentTree {
	int trnode[MAXN * 50];
	int ls[MAXN*50], rs[MAXN*50];
public:
	int root[MAXN], cnt;
#define mid ((l +r) >> 1)
	void merge(int &p, int &q, int l, int r) { 
		if (!p || !q) return p = p + q, q = 0, void(); 
		if (l == r) {
			trnode[p] += trnode[q];
			q= 0;
			return;
		}
		merge(ls[p], ls[q], l, mid), merge(rs[p], rs[q], mid + 1, r);
	}
	void update(int &root, int l, int r, int x, int val) {
		if (!root)
			root = ++cnt;
		if (l == r)
			return  trnode[root] += val, void();
		if (x <= mid)
			update(ls[root], l, mid, x, val);
		else
			update(rs[root], mid + 1, r, x, val);
	}
	int query(int root, int l, int r, int x) {
		if (!root)
			return  0;
		if (l == r)
			return trnode[root];
		if (x <= mid)
			return query(ls[root], l, mid, x);
		else
			return query(rs[root], mid + 1, r, x);
	}
} tr[2];
/**/
int ans[MAXN], w[MAXN];
void calc_ans(int u, int fa) {
	for (int i = head[u]; ~i; i = edge[i].nxt) {
		int v = edge[i].to;
		if (v == fa)
			continue;
		calc_ans(v, u);
		tr[0].merge(tr[0].root[u], tr[0].root[v], 1, n);
		tr[1].merge(tr[1].root[u], tr[1].root[v], -n, 2 * n); //注意两个的范围不一样
	}
//	auto val = ;
	if (dep[u] + w[u] > n)
		ans[u] = 0;
	else
		ans[u] = tr[0].query(tr[0].root[u], 1, n, dep[u] + w[u]);
	ans[u] += tr[1].query(tr[1].root[u], -n, 2 * n, dep[u] - w[u]);
}
signed main() {
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	memset(head, -1, sizeof(head));
	cin >> n >> m;
	for (int i = 1, u, v; i < n; ++i)
		cin >> u >> v, add_edge(u, v), add_edge(v, u);
	for (int i = 1; i <= n; ++i)
		cin >> w[i];
	init();
	for (int i = 1, s, t; i <= m ; ++i) {
		cin >> s >> t;
		int ances = lca(s, t);
		tr[0].update(tr[0].root[s], 1, n, dep[s], 1);
		tr[0].update(tr[0].root[ances], 1, n, dep[s], -1);
		tr[1].update(tr[1].root[t], -n, 2 * n, 2 * dep[ances] - dep[s], 1);
		tr[1].update(tr[1].root[dp[ances][0]], -n, 2 * n, 2 * dep[ances] - dep[s], -1);// 注意lca
	}
	calc_ans(1, 0);
	for (int i = 1; i <= n; ++i)
		cout << ans[i] << ' ';
	return 0;
}