浅谈导数

导数的一般定义及几何意义

引入

我们在初中学一次函数的时候，知道有一个东西叫做斜率。令在某一次函数上的两点分别为 \((x_0, y_0)\) ， \((x_1,y_1)\) ，则它的表达式为 \(k = \large{\frac{y_0 - y_1}{x_0 - x_1}} = \large{\frac{\Delta y}{\Delta x}}\) 。通过斜率我们轻易的看出函数在某一刻的变化趋势，但在面对类似二次函数这样的函数时，我们似乎求不出它们的斜率，也仅仅能从函数图像上看到它们的变化趋势，但事实真的是这样吗？

正片

在我看来，导数是斜率的扩展，为什么?继续看
在面对二次函数这样变化不为线性的函数时，如果想探究其瞬间变化情况，可以选择做切线（如图所示）

那么，由此我们便可以引出导数的概念了

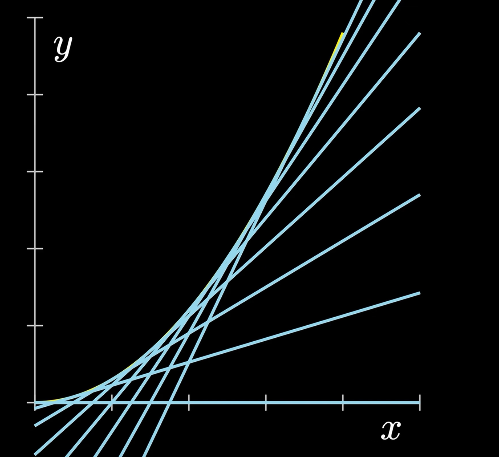
导数的定义

假设函数 \(y = f(x)\) 在点 \(x_0\) 处的邻域内有定义，当自变量 \(x\) 在 \(x_0\) 处取得增量 \(\Delta x\)，相应的函数取得增量 \(\Delta y\)，如果 \(\frac{\Delta y}{\Delta x}\) 在 \(\Delta x \to 0\) 时的极限存在，那么称函数 \(y = f(x)\) 在点 \(x_0\) 处可导。

一些发现

看起来是不是就是天书，但可以总结为一个公式

\[f'(x) = \lim\limits_{\Delta x \to 0} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} \]

你会发现这一串 \(f(x_0 + \Delta x) - f(x_0)\) 刚好不就是函数 \(f(x)\) 的增量 \(\Delta y\)吗？
那么公式就会变为

\[f'(x) = \lim\limits_{\Delta x \to 0} \frac{\Delta y}{\Delta x} \]

还记得点斜式公式吗，其实这两个就是等价的，所以回收开头 导数可以粗略的看作函数在某处切线的斜率
当然导数有一个更加严谨但比较晦涩难懂的定义，就不提了。

形象理解

很好，那你就已经知道导数的基础了，那我们形象的理解一下

我们做了一条二次函数，在上面取了一点$(1,0.3)$，做了切线，但是只知道一点无法求出斜率，所以我们再取一点 $(3,2.7)$

由点斜式求得两点连线的的斜率 $k_1 = 1.2$，但发现误差很大，于是我们发现只要两点越近，误差越小 所以带入公式得 $$ k = \lim_{\Delta x \to 0} \frac{0.3(x + \Delta x)^2 - 0.3x^2}{\Delta x} = \lim_{\Delta x \to 0} (0.3\Delta x + 0.6x) $$ 我们又可以发现，当 $x$ 趋之于 $0$ 的时候 $0.3\Delta x$ 可以忽略不记 ， 所以该函数在 $(1,0.3)$ 求的的导数 $$ f'(x) = 0.6x $$ 下面是一些常用函数和符合函数的导数

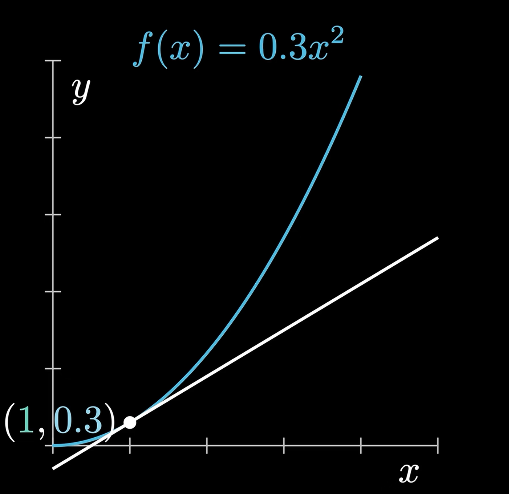
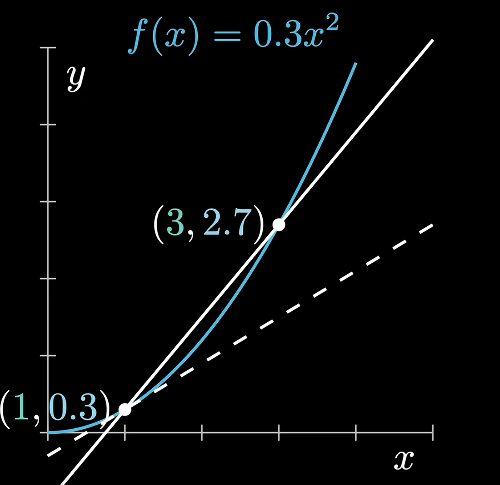
常用函数的导数

\(f(x)\)	\({f(x)}'\)
\(y = x ^ n\)	\({y}' = n \times x ^ {n - 1}\)
\(y = \sin{x}\)	\({y}' = \cos{x}\)
\(y = \cos{x}\)	\({y}' = -\sin{x}\)
\(y = a ^ x\)	\({y}' = a ^ x\ln a\)
\(y = e ^ x\)	\({y}' = e ^ x\)
\(y = \log_{a}{x}\)	\({y}' = \frac{1}{\large{x\ln{a}}}\)
\(y = \ln x\)	\({y}'=\frac{1}{\large{x}}\)

复合函数的导数

\(y = f(x) \pm g(x)\)	\(y'= f'(x) \pm g'(x)\)
\(y = f(x)g(x)\)	\(y'= f'(x)g(x) + f(x)g'(x)\)
\(y = \frac{\large{f(x)}}{\large{g(x)}}\)	\(y' = \frac{\large{f'(x)g(x)-f(x)g'(x)}}{\large{g'(x)}^2}\)
\(y=f(u(x))\)	\(y=u'(x)f'(x)\)

注意：\(\Delta x\) 不为0， 只是无穷接近0

未完持续

后记

理解导数仅仅只是开始，导数是是一个数学工具，十分有用。但碍于篇幅，其复杂公式就不一一赘述。
本人能力不足，有用词不精准或有知识性错误请指出
推荐观看Bilibili上的视频，比较形象有意思，本文一些图片引用自其中