并查集
并查集
2022.10.10 新增带权并查集(然鹅咕到了10.16)
2024.12.13 可持久化并查集!!!!!
1.含义
2.操作
查询()
int get(int x){
if(fa[x]==x)//fa[]为father数组用来存根
return x;
return get(fa[x]);
}
合并()
fa[get(y)]=get(x);
初始化()
for(int i=1;i<=n;i++)fa[i]=i;
3.一些优化
其实优化前的并查集并不迅捷
一次查询就能达到O(n)的复杂度
而一道题中就会有成千上万次合并和查询
复杂度不堪想象 这时就需要路径压缩和按秩合并了
路径压缩
int get(int x){
if(fa[x]==x)
return x;
return fa[x]=get(fa[x]);
}
原理
实际上,我们只关心每个集合对应的“树形结构”的根节点是什么,并不关心这棵树的具体形态——这意味着下图中的两颗树是等价的:
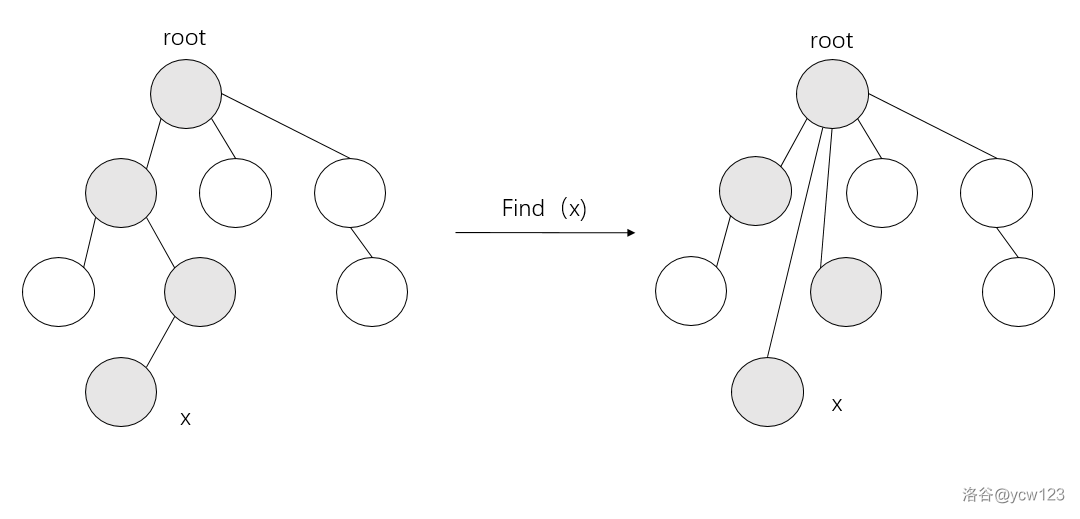
因此,我们可以 在每次执行 find 操作的同时,把访问过的每个节点(也就是所查询元素的每个祖先)都直接指向树根, 即把上图中左边那棵树变成右边那颗。
采用路径压缩优化的并查集,每次 find 操作的平均复杂度为 \(O(\alpha(n))\) 。
按秩合并
void merge(int x,int y){
int fx=get(x),y=get(y);
if(dep[fx]>dep[fy])swap(fx,fy);
fa[fx]=fy;
if(dep[fx]==dep[fy])dep[fy]++;
}
合并的优化方式是按秩合并,这种优化可以忽略,不去使用它。 在数据量非常大,且数据刁钻时,可考虑加上这个优化,否则,路径压缩足矣
原理
优化方法是创建一个dep数组维护每个集合树的深度。
在合并时,将深度小的树作为深度大的的儿子, 最后树的总深度仍是最大的那个深度,这样,在find时,会提高效率。
若两颗树的深度相同,则谁做谁的儿子都可以,只需将其深度加一即可
文中 α为阿克曼函数的反函数,一般认为不会超过5.
4.例题
种类并查集
普通并查集解决了是否为亲戚的问题
可如果想知道集合间的具体关系就要运用种类并查集了(其实带权并查集也行)
1.区别
① 种类并查集需要根据关系种类开2~n倍的father数组
② 种类并查集在合并时需要多种关系同时转移
如 朋友的朋友是朋友,敌人的敌人是朋友;
③种类并查集初始化要依据2~n倍的father数组大小
2.应用
需要多种关系同时存在,且关系间可相互转变的集合问题
3.实现
以一道水题举例
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
int fa[1500000];//1~n 为同类 n+1~2n 为食物 2n+1~3n 为天敌
//得:n+1~2n吃2n+1~3n;
int get(int x){//找祖先
if(fa[x]==x)return x;
return fa[x]=get(fa[x]);
}
int main()
{
int n,k,x,y,a,ans=0;
cin>>n>>k;
for(int i=1;i<=3*n;i++){//初始化
fa[i]=i;
}
for(int i=1;i<=k;i++){
cin>>a>>x>>y;
if(x>n||y>n||(a==2&&x==y)){//如果 x,y不在n中或自己吃自己,则为假;
ans++;//谎言数++
continue;//没有在判断下去的必要了
}
if(a==1){//如果说明x,y是同类
if(get(x)==get(y+n)||get(x)==get(y+2*n)){//如果y的天敌或食物是x,则为假
ans++;
}
else{//否则,x和y是同类
fa[get(y)]=get(x);//x,y是同一种
fa[get(y+n)]=get(x+n);//x,y的食物是同一种
fa[get(y+2*n)]=get(x+2*n);//x,y的天敌是同一种
}
}
if(a==2){//如果说明x吃y
if(get(x)==get(y)||get(x)==get(y+n)){//如果x,y是同类或y吃x,则为假
ans++;//谎言数++
}
else{//否则
fa[get(y+2*n)]=get(x);//y的天敌是x
fa[get(y+n)]=get(x+2*n);//y的食物是x的天敌
fa[get(y)]=get(x+n);//y是x的食物
}
}
}
cout<<ans;
return 0;
}
就是一个关系相互转变的过程
例题
带权并查集
顾名思义,就是有边权的并查集(也可以基本代替种类并查集)
操作
与普通并查集不同,在查询和合并时需要更新到根节点的距离,不同的题目有不同的权值计算方式,应结合实际分析
例题
可持久化并查集
前置知识
1.可持久化数组(可持久化线段树)
可持久化数组,支持基于某一历史版本的单点修改与单点查询,是实现可持久化并查集的基础.在这里不再做讲解。
问题引入
看到题目名字合并查询操作
考虑并查集,回溯历史版本,可持久化数据结构的基本操作
直接用可持久化线段树暴力修改和查询只需要单点修改与单点查询,但显然时间不允许,考虑优化.
路径压缩不可行原因
-
路径压缩时间复杂度为均摊,并查集形态为链时,单次查询最高 \(O(N)\),若一直回溯到某个为链的时刻进行操作,时间复杂度会错误
-
路径压缩过程中修改最多有 \(N\) 个在可持久化线段树上则需要新建 \(N log N\) 个节点 节点数最多达到 \(MNlogN\) 个显然开不下.
按秩合并
1. 按深度合并
较好写,也是我所采取的的方法
2.按子树大小合并
据说常数小
3. \(rand()\)
神秘
注意事项
- 合并时不能在修改节点父亲的同时更新深度,会导致时间复杂度错误
- 只有在两棵子树深度相等时才更新深度
- 若两者已在同一集合中记得继承版本后再跳过


 浙公网安备 33010602011771号
浙公网安备 33010602011771号