十二重计数法
问题背景:
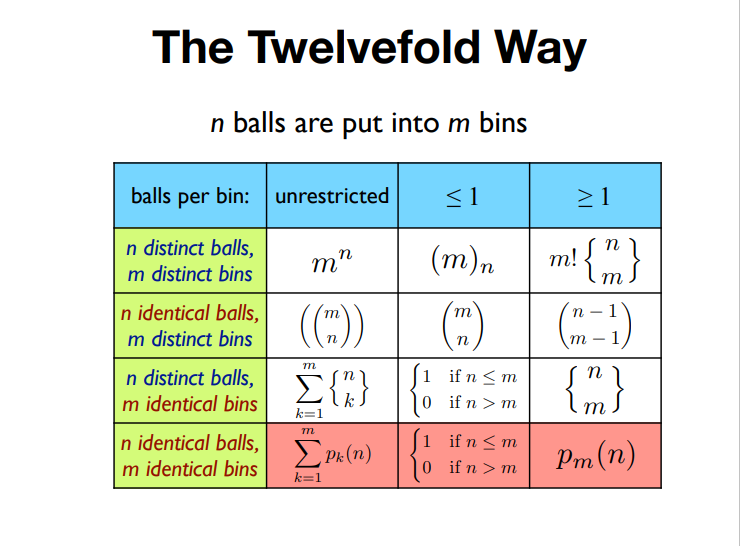
(组合版本)\(n\) 个小球放入 \(m\) 个盒子中。
(集合版本)\(n\) 元集合映射到 \(m\) 元集合。
有 \(12\) 种对方案的计数方式。球和盒子是否相同(意思是,对于两个相同的球,交换其映射对象得到的方案视为一种)有四种;限制方式(无限制;每个盒子放 \(\le 1\) 个球/单射;每个盒子放 \(\ge 1\) 个球/双射)有三种。
这些计数方式构成了最经典的十二重计数法,也就是最经典的方案计数问题。
基本定理
乘法原理:两个集合做笛卡尔积(笛卡尔积:对于两个单位元分别为 \(\epsilon_1, \epsilon_2\) 的集合 S,T 的笛卡尔积 \(S\times T\) 定义为 \(\{(\epsilon_1, \epsilon_2)|\epsilon_1 \in S, \epsilon_2 \in T\}\))的结果的大小等于原来两个集合大小乘积。
加法原理:两个不交集合的并的大小等于这两个集合大小之和。
双射原理:如果存在双射:\(\phi :S \rightarrow T\),那么 \(|S| = |T|\)。计数最聪明的原理。
(单射原理、满射原理:如果把双射换成单射/满射,那么 \(|S| \le |T|\) / \(|S| \ge |T|\))
基本性质和观察
对于“相同”和“不同”的转化。
考虑球不同和球相同的公式之间有什么关系:为什么不是除以 \(n!\) 的关系?因为如果在有标号的时候球 \(1,2\) 都映射到了盒 \(k\),那么当无标号的时候这个方案并不能除以 \(2!\),而是一个方案对应着一个方案。
那么如果是单射就没有这个问题了,因此对于第一行第二列,等于 \(n!\) 乘以第二行第二列。同理,是满射的话可以除以 \(m!\)。对于第一行第三列,等于 \(n!\) 乘以第三行第三列。
对于球不同盒子也不同的问题,并没有一个代表性的模型来描述;对于球相同盒子不同的问题,描述的模型是插板法/不定方程解的个数。对于球不同盒子相同的问题,描述的模型是集合的分拆。(特点不是分拆的对象是集合,而是分拆的结果是一个集合,并且分拆的对象是 \([n]\))对于球不同盒子也不同的问题,描述的模型是整数的分拆。这个是最难的,甚至没有封闭形式的答案。
对于后面三种,答案的形式都有自己鲜明的特色:组合数,第二类斯特林数,分拆数。其中单射这一列和该行主旋律稍有背离。而无限制和满射只是规定了映射入集合的大小,会比较有关联。
需要求这些东西的 \(2 \times 10^5\) 是很困难的,需要多项式。但是 \(O(n^2)\) 的公式是要会的。
第一行
第一个是 \(m^n\),乘法原理。
注意第二个是 \((m)_n\) 表示 \(m\) 的 \(n\) 次下降幂。这个东西并不是三大原理推出来的,而是一个具有树形结构,有后效性的东西。不要忽略了这一点。
第三个直接由第三行往上推。所以和斯特林数是有关系的。
插板法
\(n\) 个小球放入 \(m\) 个箱子里的满射是一个 \(\dbinom{n-1}{m-1}\) 同时也是 \(a_1+...+a_m=n\) 的正整数解个数。
单射呢?其实就是选择 \(m\) 个盒子里面放入一个球。
无限制的话,其实是非负整数解个数。那么你再加入若干个球就好了。
这里针对不定方程这个模型有一个延伸,就是考虑 \(\le n\) 的方案数。这时候加入一个“垃圾桶”元素表示扔掉就好了。如果是正整数解,那么 \(n\) 也要 \(+1\)。对正整数解也就是 \(\dbinom{(n+1)-1}{(m+1)-1}\),非负整数解也就是 \(\dbinom{n+(m+1)-1}{(m+1)}\)。
这个东西可以双射到多重集计数模型。多重集长这样:
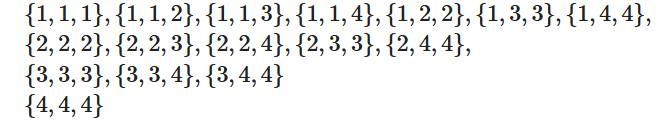
考虑每一个多重集都映射到一个数组 \({c}\) 表示 \(i\) 选了几次。其中应当满足的条件是 \(c_1 + ... + c_n = m\)。
这也就是非负整数解的个数。
还有一种映射方法,可以搞成一个单射。方法是做一遍前缀和(弄成非降序列)然后对 \(s_i += i\)(弄成上升序列)。也可以证明这个数组除了最后一个数之外也就是球无标号盒子有标号的单射个数,其中球数是 \(n + m - 1\),盒数是 \(n - 1\)。

集合的分拆
具体而言,是 \([n]\) 的分拆,分拆成若干个无标号的集合。拆成 \(m\) 份的方案数是第二类斯特林数,转移方程式 \(f_{n, m} = f_{n - 1, m - 1} + m f_{n - 1, m}\)(放到之前的子集里面,每一个子集都只有一种放的方式)
顺便提一嘴,第一类斯特林数“\(n\) 轮换 \(m\)” 的公式是,\(f_{n, m} = f_{n - 1, m - 1} + (n - 1) f_{n - 1, m}\)。
贝尔数是 \(\sum \limits_{i = 1} ^{n} S2_{n, i}\)。
分拆数
整数 \(n\) 的分拆为 \(m\) 个无标号份(可以看成是排好序了)的方案数记作 \(p_m(n)\)。
这个公式的推导过程是很精妙的。我们考虑 \(n-1\) 的分拆并不会对 \(n\) 的分拆构成子问题。不妨考虑分拆方案中最小的那个数:如果是 \(1\),方案数为 \(p_{m - 1}(n-1)\),否则对分拆结果每一个数都减去 \(1\) 化为 \(p_{m-k}(n)\) 的子问题。
因此 \(p_m(n) = p_{m - 1}(n - 1) + p_{m - k}(n)\)。
这个东西还可以用另外一个视角看待:完全背包。用 \(1 \sim n\) 去填满 \(n\) 体积的背包,并且用 \(m\) 个物品。如果看做 \(m\) 次卷积,目标多项式的定义是用 \(i\) 种物品填满 \(j\) 体积的方案数,转移多项式是一种物品填满 \(j\) 体积的方案数,这里面会算重。但是我们如果做的是一个完全背包,有很好的优势。(如果需要记录 \(m\) 那么是三维的,但是如果不需要记录 \(m\) 只是一个完全背包的结果)
注意到这个“算重”也是可以利用的。考虑这样一个问题:(CF某个F)四个角,每个角构造一个杨表,加起来大小为 \(n\) 的方案数。这样我们做出一个长度为 \(n\) 的表示一次填满 \(i\) 体积的方案数的数组,然后做四次卷积即可。
这是 jiangly 的写法。

(还没有搞懂原理)
对分拆数的大小有个概念:对于 \(n\),\(f_n = \sum \limits_{i \in [1, m]} \sum \limits_{j \in [1, i]} p_j (i)\) 的量级:
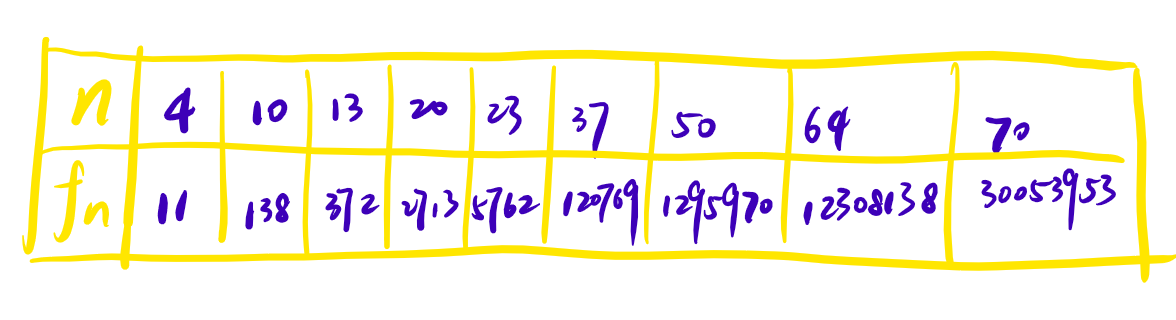
应用:证明状态数。考虑选择若干个数使得其加起来不超过 \(50\),并且相等的数是相同的。那么状态数是 \(f_{50}\),可以接受。
分拆数具象化到杨表上之后,有转置,并且转置构成双射。因此有定理:
- 分拆之后最大的数是 \(k\) 的方案数为 \(p_k (n)\)。
- \(p_k(n)=\sum \limits_{j=1}^k p_j(n-k)\)。这个就是对杨表做一次前 \(k\) 列加一个元素的结果。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号