矩阵与 DDP
1 矩阵和矩阵快速幂
1.1 矩阵乘法
矩阵乘法满足:
因此我们可以让
而 \(transform^{n} = transform^{k} \times transform^{n - k}\) 。
也就是满足结合律。
我们考虑为什么满足结合律。不妨分析 \(\mathbf{(A \times B) \times C)}_{1,1}\) 和 \(\mathbf{A \times (B \times C)}_{1,1}\) 是否相等。
推一推,假设 \(\mathbf{A}\) 的长度和宽度分别为 \((n,m)\),\(\mathbf{B}\) 的长度和宽度分别为 \((m,l)\),\(\mathbf{C}\) 的长度和宽度分别为 \((l,p)\)。
那么
这一步是关键的。由于 \((a+b+...) \times c = ac + bc + ...\),所以上式等于:
那么容易证明原等式成立。
事实上,若“乘”和“加”重新定义,那么只要满足“乘”对“加”的分配律,那么就可以进行矩阵乘法。
例如:
“乘” 变成 “加”,“加” 变成 “\(\max\)”,此时因为有
因此可以。
再例如,“乘” 还是 “乘”,“加” 变成 “\(\max\)”,行不行呢?注意到当所有数都非负的时候有
因此这时才可以使用这样的矩阵乘法。
当两个操作分别为 \(+\),\(\max\) 时,单位矩阵的构造:
理由:这个矩阵乘上任意矩阵都等于那个矩阵。
还可以是 \(\oplus, \times\) (搬到 \(\N_2\) 上做)
1.2 矩阵求逆
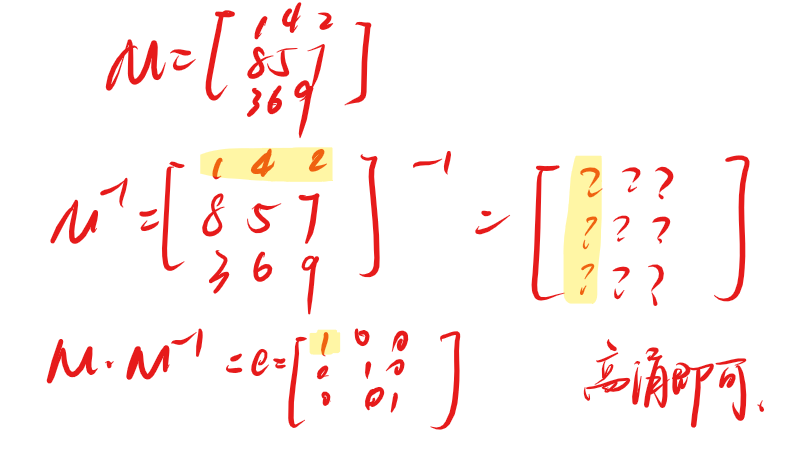
时间复杂度 \(O(n^3)\)。
1.3 矩阵快速幂
一般做矩阵快速幂的时候,是需要“把母矩阵和一个答案矩阵相乘赋值给答案矩阵”这个操作执行 \(n\) 次。这时我们可以使用矩阵快速幂优化这个过程。
传入参数的时候不引用,就不会改变母矩阵本身的值,可以重复利用。
一般为了方便会把矩阵的大小固定下来,如果 \(2\times 2\) 的矩阵乘 \(2\times 1\)的矩阵,大小不一致会很麻烦,用 \(0\) 把第二个矩阵补上变成都是 \(2 \times 2\) 的,不会影响矩阵对应位置的数字,只需要记录矩阵长=宽 \(matn=2\) 即可。
时间复杂度 \(O(\log n \times matn^3)\)。
我们可以建立一个 mat 结构体,把一些 operator 都封装在结构体里面。我们先学习一下封装的语法:
struct trial {
int a, b, c;
int d[6][6];
inline trial(int _a, int _b, int _c): a(_a), b(_b), c(_c) {
f(i, 1, 5) f(j, 1, 5) d[i][j] = i + j;
}
};
signed main() {
trial x(1, 2, 3);
cout << x.a << " " << x.b << " " << x.c << endl;
f(i, 1, 5) f(j, 1, 5) cout << x.d[i][j] << " \n"[j==5];
}
其中括号里面可以传入参数,冒号是在参数列表和函数内部之间的方便赋值的东西,函数内部也可以做点事情。
然后是矩阵快速幂模板,其中乘法用 \(r\) 是常数优化:
struct mat {
int a[5][5];
mat() {memset(a, 0, sizeof(a));}
mat operator* (mat &b) {
mat c;
f(i, 1, 4) f(k, 1, 4) {
int r = a[i][k];
f(j, 1, 4) {
c.a[i][j] += r * b.a[k][j];
c.a[i][j] %= mod;
}
}
}
mat operator^ (int k) {
mat x, ans;
//ans 赋值为单位矩阵
f(i, 1, 4) ans.a[i][i] = 1;
f(i, 1, 4) f(j, 1, 4) x.a[i][j] = a[i][j]; //也可以用 mat x = *this;。还可以在下面把 x 直接换成 (*this)。
while(k) {
if(k & 1) ans = ans * x;
x = x * x;
k >>= 1;
}
return ans;
}
};
1.4 用矩阵表示线性变换
ABC288G
对序列 \(A_0, ..., A_{3^n - 1}\) 做变换得到:
\(B_i = \sum \limits_{neighbor(i, j)} A_j\),其中 \(neighbor(i, j) = 1\) 当且仅当对于 $ \forall k = 0, ..., n - 1$ 有 \(i, j\) 的三进制中第 \(k\) 位之差不超过 \(1\)。
分析:可以从多维空间的角度,但这里有一个可供推广的思路:每一维度乘上了这样一个矩阵(线性变换都有这样的特征)

那么每一个维度乘上矩阵的逆即可,这个逆可以手算。
2 动态 DP
转移使用矩阵表示之后出现了结合律,于是可以灵活改变其中的某一些矩阵。以一个例题来分析:
例题1:最大子段和问题,区间询问版本。
https://www.luogu.com.cn/problem/SP1043
\(1 \le n, q \le 4 \times 10^5\)
考虑 dp。首先考虑简单版本:令 \(dp_i\) 表示以第 \(i\) 个元素为结尾的最大子段和。
根据矩阵乘法的重新定义,我们可以把它写成矩阵,其中“乘”->“加”,“加”->“\(\max\)”。也就是:
考虑求
有
也就是我们对于每次询问需要求出 $ \mathbf{A_R}\mathbf{A_{R-1}}...\mathbf{A_{L+1}}$。
注意到 \(\mathbf{A_i}\) 和 \(a_i\) 有关,且只和 \(a_i\) 有关。怎么求?考虑我们做序列连续和怎么做。前缀和/差分;树状数组;线段树...
考虑前缀积,但是由于矩阵不一定存在逆(需要高斯消元方程有解),不行。
考虑树状数组,我们复习一下树状数组的性质,发现差分需要有逆操作,但是矩阵不一定存在逆,不行。
于是我们可以用线段树。每一个节点维护一个矩阵,上传操作是矩阵乘法。不需要修改,只需要查询区间积即可。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e12;
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
struct mat {
int a[5][5];
mat() {
memset(a, 0xcf, sizeof(a));
}
mat operator* (mat b) {
mat c = mat();
f(i, 1, 2) {
f(k, 1, 2) {
int r = a[i][k];
f(j, 1, 2) {
c.a[i][j] = max(c.a[i][j], r + b.a[k][j]);
}
}
}
return c;
}
mat operator^ (int b) {
mat c = mat(), x = *this;
f(i, 1, 2) c.a[i][i] = 0;
while(b){
if(b&1)c=c*(*this);
(*this)=(*this)*(*this);
b>>=1;
}
return c;
}
};
struct sgt {
mat A = mat();
}t[300010];
int y[300010];
void build(int now, int l, int r) {
if(l == r) {
t[now].A.a[1][1] = t[now].A.a[1][2] = y[l];
t[now].A.a[2][1] = -inf; t[now].A.a[2][2] = 0;
return;
}
int mid = (l + r) >> 1;
build(now * 2, l, mid);
build(now * 2 + 1, mid + 1, r);
t[now].A = t[now * 2].A * t[now * 2 + 1].A;
}
mat query(int now, int l, int r, int x, int y) {
if(l >= x && r <= y) {
return t[now].A;
}
if(l > y || r < x) {
mat ret = mat();
f(i, 1, 2) ret.a[i][i] = 0;
return ret;
}
int mid = (l + r) >> 1;
return query(now * 2, l, mid, x, y) * query(now * 2 +1, mid + 1, r, x, y);
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
time_t start = clock();
//think twice,code once.
//think once,debug forever.
int n; cin >> n;
f(i, 1, n) cin >> y[i];
build(1, 1, n);
int m; cin >> m;
f(i,1,m){
int l,r;cin>>l>>r;
mat tar = mat();
tar.a[1][1] = y[l], tar.a[2][1] = 0;
mat rat = query(1, 1, n, l + 1, r);
rat = rat * tar;
cout << rat.a[1][1] << endl;
}
time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
现在考虑原问题怎么做。显然可以求出区间矩阵乘积,然后乘以初始矩阵即可。
例题2:带单点修改。
\(q\) 次修改单点 \(a_i\) + 询问。
\(1 \le n, q \le 2 \times 10^5\)
每次在线段树中单点修改 \(A_i\) 即可。
CF1814E
比赛的时候遇到的一道动态dp,场切了。
转移式子是
显然可以表示为矩阵 \(\min, +\) 乘法。问题是要搞清楚左右乘。但是不小心写成右乘也没关系,线段树网上合并的时候改成右边乘以左边即可。
#include<bits/stdc++.h>
using namespace std;
#define int long long
//use ll instead of int.
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 1e16;
//#define cerr if(false)cerr
//#define freopen if(false)freopen
#define watch(x) cerr << (#x) << ' '<<'i'<<'s'<<' ' << x << endl
void pofe(int number, int bitnum) {
string s; f(i, 0, bitnum) {s += char(number & 1) + '0'; number >>= 1; }
reverse(s.begin(), s.end()); cerr << s << endl;
return;
}
template <typename TYP> void cmax(TYP &x, TYP y) {if(x < y) x = y;}
template <typename TYP> void cmin(TYP &x, TYP y) {if(x > y) x = y;}
//调不出来给我对拍!
//use std::array.
int c[200200];
struct matrix {
//n = 3
int a[3][3];
matrix() {f(i,0,2)f(j,0,2)a[i][j]=inf;}
matrix operator*(matrix op) {
matrix res;
f(i,0,2)f(j,0,2)f(k,0,2){
cmin(res.a[i][j],a[i][k]+op.a[k][j]);
}
return res;
}
matrix(int cim1, int cim2) {
a[0][0]=inf;a[0][1]=cim1;a[0][2]=cim1+cim2;
a[1][0]=0;a[1][1]=inf;a[1][2]=inf;
a[2][0]=inf;a[2][1]=0;a[2][2]=inf;
}
}m[200200], it;
struct sgt {
matrix t[4 * 200020];
void build(int now,int l,int r) {
// f(i,1,3)f(j,1,3)cout <<t[now].a[i][j]<<" \n"[j==3];
// cout << "(build)\n";
if(l==r){
t[now]=m[l];// f(i,1,3)f(j,1,3)cout <<t[now].a[i][j]<<" \n"[j==3];
// cout << "(after build)\n";
return;
}
int mid=(l+r)>>1;
build(now*2,l,mid);build(now*2+1,mid+1,r);
t[now]=t[now*2+1]*t[now*2];
// f(i,1,3)f(j,1,3)cout <<t[now].a[i][j]<<" \n"[j==3];
// cout << "(after build)\n";
}
void modify(int now,int l,int r,int x,matrix mat) {
if(l==r){
t[now]=mat; return;
}
int mid=(l+r)>>1;
if(x<=mid)modify(now*2,l,mid,x,mat);
else modify(now*2+1,mid+1,r,x,mat);
t[now]=t[now*2+1]*t[now*2];
}
// matrix query() {return t[1];}
}sgt;
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//freopen();
//freopen();
//time_t start = clock();
//think twice,code once.
//think once,debug forever.
int n; cin>>n;
c[0]=0;
f(i,1,n-1)cin>>c[i];
f(i,1,n)m[i]=matrix(c[i-1],i-2<0?inf:c[i-2]);
it.a[0][0] = 0;it.a[1][0] = inf; it.a[2][0] = inf;
sgt.build(1,1,n);
int q; cin>>q;
while(q--){
int k,x;cin>>k>>x;c[k]=x;
m[k+1]=matrix(c[k],k-1<0?inf:c[k-1]);
sgt.modify(1,1,n,k+1,m[k+1]);
if(k<n-1){
m[k+2]=matrix(c[k+1],k<0?inf:c[k]);
sgt.modify(1,1,n,k+2,m[k+2]);
}
matrix mt = sgt.t[1]; //sgt.query();
// f(i,1,3)f(j,1,3)cout <<mt.a[i][j]<<" \n"[j==3];
matrix res = mt*it;
cout <<res.a[0][0]*2 << "\n";
}
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
/*
2023/x/xx
start thinking at h:mm
start coding at h:mm
finish debugging at h:mm
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号