CF98E Help Shrek and Donkey

CF98E Help Shrek and Donkey

纳什均衡的应用。 首先纳什均衡就是每个人都有一个是自己的期望收益最小值最大的点；
有定理：在一个零和博弈中， 一定存在一个这样的纳什均衡点
这个题也是显然的纳什均衡博弈题。
首先， 对于一个人我们有三种不同的操作

1. 直接翻牌
2. 询问一张自己没有的牌
3. 询问一张自己有的牌（达到迷惑对手的目的）
   然后对于后面两种操作， 后手都有对应的认为（认为是真的还是假的）

列出期望的表格之后

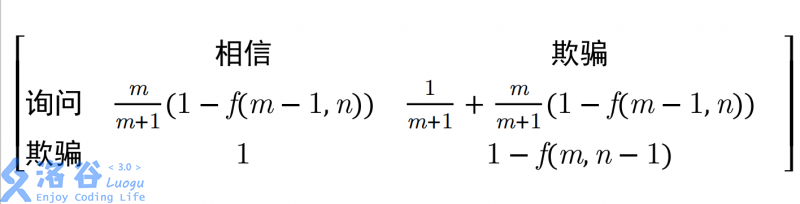
发现不可能在 \(n, m \neq 0\) 的时候翻排， 因为那样只有 \(1/ (m + 1)\) 的收益。
然后列方程求纳什均衡点就可以了

图片来源网上

/*
Author: Zcus
Blog: cnblogs.com/Zcus
*/

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'

//#define int long long
//#define FILE
#define fi first
#define se second
#define pb push_back
#define pii pair<int, int>
#define mp make_pair
#define debug(x) cout << #x << " = " << x << endl
#define For(i, x, y) for (int i = x; i <= y; i++) 
#define Rep(i, x, y) for (int i = x; i >= y; i--) 
#define file(FILE_NAME) freopen(FILE_NAME".in", "r", stdin), freopen(FILE_NAME".out", "w", stdout)
#define filein(FILE_NAME) freopen(FILE_NAME".in", "r", stdin);
#define fileout(FILE_NAME) freopen(FILE_NAME".out", "w", stdout);

template<class T> inline bool Chkmax(T& x, const T& y) { return x < y ? x = y, true : false; }
template<class T> inline bool Chkmin(T& x, const T& y) { return x > y ? x = y, true : false; }


const int maxn = 2020;
double dp[maxn][maxn];
int vis[maxn][maxn];
int n, m;

void DP(int n, int m) 
{
    
	if (vis[n][m]) return void();
	vis[n][m] = 1;
	if (m == 0) 
	{
		return dp[n][m] = 1.0, void();
	}
	if (n == 0)
	{
		return dp[n][m] = 1.0 / (m + 1), void();
	}
	DP(m, n - 1); DP(m - 1, n);
	double p = dp[m][n - 1] / (dp[m][n - 1] + 1.0 / (m + 1));
	dp[n][m] = p * m * 1.0 / (m + 1) * (1.0 - dp[m - 1][n]) + 1.0 - p;
}
int main() 
{
//	ios :: sync_with_stdio(0); cin.tie(0);
	cin >> n >> m;
	DP(n, m);
	printf("%.9lf %.9lf", dp[n][m], 1.000000000 - dp[n][m]);
	return 0;
}