巨佬的博客:https://www.luogu.com.cn/blog/CFA-44/yi-suo-chang-jian-tao-lu https://www.luogu.com.cn/paste/8hnex65m
- 二分:
- maximize minimum 或者 minimize maximum 优先考虑二分
- 二分性,答案取值范围的一段前缀/后缀合法,或者有单调性
- 计数 DP:考虑所谓的“不可划分的整体”,围绕这个整体划分子问题
- 例如 CF888F,就是将两个直接相连的点中间的所有点作为整体
- 前面对后面有影响(即,正着做有后效性)?
- 考虑倒着做
- 例如 CSP-S 2020 T4,就是倒着考虑每一条蛇到目前的最终局面时是否还健在,如果是,则继续;否则,将目前最终局面改成它做决策时的局面
- 猜出了一个贪心策略?
- 从最优性(是否可能存在一个更优的方案)和可行性(是否可以按照策略构造出一个最优方案)证明
- 相邻交换得到了一个含 max/min 的式子?
- 分类讨论所有可能的大小关系,通过推导与/或关系来得到一个确定的全序关系
- 怎么搞都要 2n 枚举子集?
- 这个子集也许有性质,例如一定是连续区间
- 期望 dp?
- 倒着设计状态和转移,已知推未知
- 所有子集的子集
- 复杂度不是 O(2n×2n),是 O(3n)
- kth 相关
- 二分答案转换成 0/1 最大子段和等问题
- 中位数相关
- 二分答案转换成 -1/1 最大子段和等问题
- 图论题中有一个数非常小
- 考虑利用它拆点
- 对所有排列考虑 / 将原序列重排
- 原来的顺序没关系了,可以排序等等方式处理
- V - E 容斥
- 对于每个点统计一遍贡献,再对每一个边统计一下贡献,两者相减后所有连通块的贡献只被算 1 次
- 对于树上连通块交的相关计数很有用
- 重心只能在以根为链头的重链上
- 两点集直径在两点集各自的直径的 4 个端点中取一对点,点集中距离一个点最远的点一定是点集的直径的两个端点之一。
- 多个价值维度均合并为一项之后互相干涉并产生价值,可以把合并出的一项作为坐标建系,例如 P5540。
- “某些元素在某时刻消失”倒流变成“某些元素在某时刻出现”有时很关键。
- 竞赛图缩点后是一条链
- 不仅区间加/减可以考虑差分,矩形加/减也可以。
- 子段和 → 整体 - 前缀 - 后缀(Topcoder 14719)
- 后面覆盖前面 → 倒过来 → 只和第一次有关系
- lcm(1,2,3,⋯ ,18)∼O(107),遇到取模+类似数据范围可以考虑这个复杂度
- 处理平方数的一种 hash:维护一个完全异或性函数,对于所有质数 p,f(p) 取任意值。
- 数据范围大也可以考虑最大流,特殊图最大流不好求可以转特殊图最小割,有一些可以用数据结构维护。
- DP 被卡空间了立刻考虑调换维度之后滚动。
- 奇怪的不能 FMT/FWT 的卷积形式可以考虑类似 karatsuba 的方式做到 3n。gym102129A
- 和时间有关的游走问题考虑建时间轴。(按理说这不是个很直接的暴力想法吗……为啥我想不到啊/kk)
- k 次方求和可以转 k 个独立方案的组合
- 根节点复制 k 份 -> 孩子独立
- 本质不同border形态数量是亚指数级别
- 离线数子区间:枚举询问右端点,线段树维护每个点作为目前扫到的多少个子区间的左端点
- 遇到 mex 的时候可以往二进制上想
- dfs 序背包:维护 dfs 序在当前点之前的信息,每次加入当前点信息并依次递归子树更新(EINOIP2022D1T4)
- 静态区间查询只能往一个方向加东西的时候考虑对称性(UNR#6 D1T3)
构造
- 差分约束/拓扑排序/高斯消元(省选2021 d1t2,某个 gym 题,CF1635E)
- 格雷码构造原理(某个洛谷月赛 C,某个联测 T1)
- 打表找规律(P3599)
- 观察/模拟样例(P5441,P8103)
- 强化/转化限制(CF1641B 转化为排序,P8282 改为最优化一个东西)
- 从特殊情况出发(CF1583F)
- 增量法(完全图构造先红后蓝哈密顿路那个题)
猜结论/性质
- 交 换 差 分/前缀和
- max/min 单调栈 -> 笛卡尔树,笛卡尔树上左链/右链一般比较有用
- 猜决策单调性(artistic partition)
- 调整/直觉(CF1442D 调整最后一个元素的位置 -> 只有一个不顶到头)
- 构造性的猜法(构造答案,部分依赖打表)
- 最优化问题简化限制:
- 它不合法,但是它同时不优于至少一个合法解,直接算进来也行(很多,比较有代表性的是 NOIP2017 宝藏)
- 分析最优性得到每一次选取的可能解集要么全部合法要么全部不合法,且可以快速判断(JOISC 2022 D2T3)
贪心
参考 https://www.luogu.com.cn/paste/8hnex65m
- 相邻交换
- 树上相邻交换:
- 先和序列上一样做。
- 由于相邻交换本身的特性,其所针对的变换通常可以合并。如果儿子排在父亲前面,合并儿子和父亲。
- 全部合并结束后按顺序选。
- 树上相邻交换:
- 超级钢琴:答案候选集合中选出最大,然后分裂集合
- 反悔贪心(P2209)
- 利用贪心想法简化问题形式(CF1632D,转化为序列切分然后 DP)
- 限制/影响最小化的思想(CF1404C:删后面不影响前面 -> 每时刻删最后一个;U202373:前面影响的限制更多 -> 优先放后面)
- 差分相关有一些需要把操作 2 个位置转化为 1 个,但是有时候也需要把操作 1 个位置转化为 2 个
- 可能贪心找不到最优解,但是能用贪心把答案用一个很小的范围界住/把一个比较大的范围内的答案都确定为同一个值,然后用一些更暴力的东西(例如 dp)(某个联测 T2的神秘 w≤300,v=1,C=1018 多重背包)
ds
- segtree
- 线段树合并
- 优化树上 dp
- 优化拓展域并查集(本质是重构树上 dp?)
- 离散化用来卡空间
- 扫描线的特殊性质
- O(nlogn) 线段树
- 大多用于静态问题
- 维护一些类似函数的东西
- e.g. CF1404C 维护常数分段函数,P5073、P4118 维护线性分段函数
- 优化线性 dp
- 大多题目是单点修改 dp 值 区间求 min/max 值,或者区间对某个值取 min/max 单点求值
- P2605 区间加单点求值
- 结合单调栈(CF1483C)(有时候可以简化操作,变为前缀/后缀取 max,复杂度不变但是常数和代码难度都会好很多)
- 优化建图
- P5284 SA 上优化建图
- 1log 区间线段树二分
- 按照一定的方向搜索 logn 个终止节点
- 如果节点中可以有答案就以它为根做整体的线段树二分,并直接返回
- 线段树合并
- fenwick tree
- 点分治
- 多数是深度上前缀查询,所以可以做
- 树状数组上倍增
- 解决一些全局线段树二分的问题
- 常数有明显优势
- P6619
- 点分治
- 分块
- 根号平衡
- O(sqrt)-O(1) 维护块上前缀和(群)/猫树(半群)
- O(1)-O(sqrt) 维护整块求和
- 根号平衡
网络流
观察数据范围比较小(1000 以下)不知所云(2e4,3e4 这种)还有个数据随机
明显不能网络流:尝试建图之后发现需要一个大于 1 的流整体分到一条边里面
优化单位流图O(EsqrtV)一个流直接连通性就可以了省选联考 2018 劈配
最大流转最小割,数据结构维护U202373、某个 pkusc 题
最大流转对偶图最短路csp2021 T4平面图最小割计数
模拟费用流费用流跑不动就模拟费用流NOI2019 序列
最短路/mst
成环的特殊 DP 转移,用最短路解决
差分约束
0/1 最短路:bfs
非负边权最长路:缩点,单个 scc 里面有正边输出 inf,否则跑 DAG 最长路
2x2 子矩阵 3 推 1:行、列分别建一列点,两列点之间建边,转化为生成树相关
dp
限制和断点有关的分段 DP 强制结尾,转移点枚举上一个,但是限制考虑下一个AGC009C
强制结尾思想可以去掉一维,代价通常是转移多一维,数据结构优化P8277
分治优化需要转移可以合并,且限制可以拆分P5979点分治可以类似优化树上 dp?(做了一些尝试,似乎在大部分情况下等价于 HLD 启发式合并)
整体 DP 状态数爆炸,但是可以滚动,而且可以数据结构整体维护转移两个人在数轴上游走,有一些点要求至少一个人到达(线段树维护)
轮廓线 DP“轮廓线”并不一定要是真正意义上的轮廓线,只是对于一个图,如果能够保证任意时刻只需要考虑很少的点就可以了通俗来讲是一个“状压露在外面的部分”的想法,通过一些手段让露在外面的不会太多两个环中间夹一个图然后计数子图那个破题
乱搞神秘状压猜一手状态个数不多,写个记搜直接过
使用一些贪心方法卡出一个答案的比较紧的界,利用这个界去除一些显然不优的状态CF1830D:黑白染色把答案下界卡到 n^2,导出同色连通块最大 O(sqrtn) 的结论
计数
容斥不好做就试着把限制反过来<=x的拆分
积和式sum prod [cond] = sum prod (1-[!cond]),打开 prod 得到容斥系数
算贡献的思想本质是交换求和顺序生成函数
数论
积性函数线性筛
i^k线性筛
Mobius 函数本质是迪利克雷差分的容斥系数μ∗1=e
欧拉函数φ∗1=n欧拉定理gcd(a,p)=1,有 a^φ(p)≡1(modp)不要求 p 是质数
扩展欧拉定理指数上套 log 层就不变了
各种套路
(不是非常全,想到就更)
数据结构
-
树状数组上二分:当前位置\(pos\)满足\(2^b|pos\),枚举下一段长度\(2^j\),其中\(j<b\),节点\(pos+2^j\)上存的值为\([pos+1,pos+2^j]\)中的贡献,如果当前值加上区间中的值满足条件,就跳到\(pos+2^j\)上继续枚举 P6619 [省选联考 2020 A/B 卷] 冰火战士
-
01trie整体+1:对于每个节点,交换01儿子,递归到原来的1儿子节点+1P6623 [省选联考 2020 A 卷] 树
-
单点修改,区间求和:有时修改和查询次数并不相同,可以进行平衡
- \(O(\log n)\)修改,\(O(\log n)\)查询:树状数组
- \(O(1)\)修改,\(O(\sqrt n)\)查询:分块,修改时只修改点值和块内和。查询时整块直接查块内值,散块暴力查询每个值
- \(O(\sqrt n)\)修改,\(O(1)\)查询:分块,修改时维护块内前缀和,块间前缀和。查询整块用块间前缀和算,散块用块内前缀和算
-
并查集:01序列上,可以把0修改成1,询问某个位置前的第一个0
-
长度为\(n\)的序列,有\(m\)次区间染色操作,求最后序列的状态
倒序枚举每个操作,用并查集维护每个位置下一个没染的地方,暴力把区间内所有没颜色的地方染色,均摊复杂度为\(O(n\operatorname\alpha(n))\)
-
-
动态开点平衡树:每个节点维护一个区间,等到分裂的时候再新建节点 链接 P7739 [NOI2021] 密码箱
-
楼房重建,用线段树维护区间单调栈,线段树update的时候线段树二分找右儿子\(\geq\)左边最大值的单调栈,复杂度\(O(n\log^2n)\) 从《楼房重建》出发浅谈一类使用线段树维护前缀最大值的算法——小粉兔 P4198 楼房重建,U237227 带修区间单调栈长度(楼房重建加强)
-
二进制分组:对于某些需要\(O(n)\)预处理,且不支持插入的数据结构(如AC自动机),可以用二进制分组实现均摊\(O(\log n)\)动态插入
新插入一个元素时,把它自己归为一组,每次判断左边的组大小是否和我一样,如果一样就合并,否则退出
\[\{8,2,1\}\to\{8,2,1,1\}\to\{8,2,2\}\to\{8,4\} \]每个元素只会被重构\(\log n\)次,插入均摊复杂度\(O(\log n)\)
-
线段树维护历史和:转化成\(kx+b\) P8868 [NOIP2022] 比赛
-
序列区间询问考虑能否线段树维护
-
cdq分治实质:可以快速(如\(O(n\log n)\))统计一个矩形内的贡献,需要统计一个直角三角形,将三角形拆成\(O(\log n)\)层矩形,每层矩形边长和为\(O(n)\)
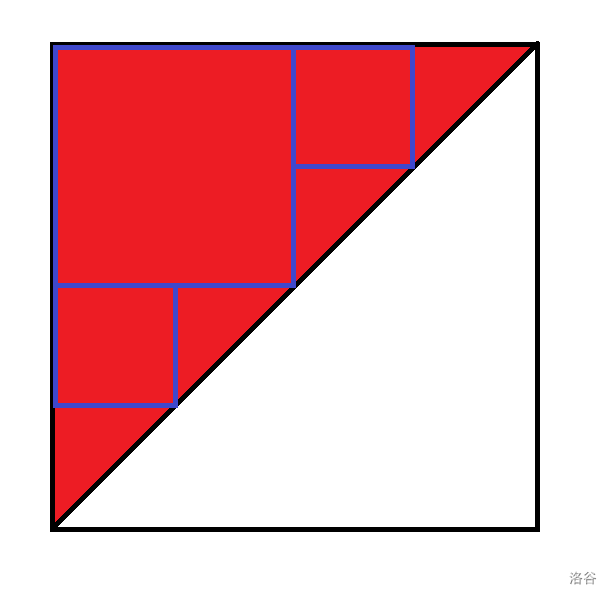
- 条状cdq:先将条分成若干个直角三角形,再做cdq
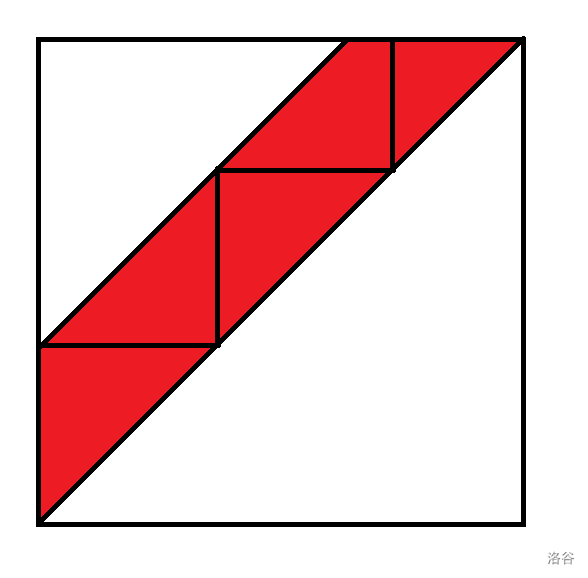
-
set-beats:线段树区间取min,区间加,查询区间和,查询区间最大值
维护区间的最大值,严格次大值,最大值个数,区间和
tag就是加法,最大值对\(x\)取min
修改时,如果取min的值要大于次大值,直接改,否则往下递归
不带区间加:\(O(n\log n)\),带区间加:\(O(n\log^2n)\)常数极小
贪心
-
相邻交换法
-
将取min或取max的不等式转换为逻辑表达式,例如:
\[\max\{A,B\}\leq C\Leftrightarrow A\leq C \&\&B\leq C \] -
可反悔贪心,把反悔选项扔到决策集合里 P1484 种树,P2209 [USACO13OPEN]Fuel Economy S
-
当限制为“到某时刻截止”时,可以考虑时光倒流,让限制变为“从某时刻开始”P1954 [NOI2010] 航空管制,P3826 [NOI2017] 蔬菜
-
超级钢琴:若干种决策,有依赖关系,且每种决策的收益小于其所依赖的前置决策
每次选择在所有当前可选的决策选一个收益最大的(用优先队列维护),将新的可选决策放入优先队列
P2048 [NOI2010] 超级钢琴,P1315 [NOIP2011 提高组] 观光公交,BZOJ3784 树上的路径
-
合并果子:决策之间满足某种单调性,用队列维护 P1090 [NOIP2004 提高组] 合并果子,P2827 [NOIP2016 提高组] 蚯蚓,
组合
- 范德蒙德恒等式运用\(\sum\limits_{i=0}^n\begin{pmatrix}k\\i\end{pmatrix}\begin{pmatrix}n-k\\i\end{pmatrix}=\sum\limits_{i=0}^k\begin{pmatrix}k\\i\end{pmatrix}\begin{pmatrix}n-k\\n-k-i\end{pmatrix}=\begin{pmatrix}n\\n-k\end{pmatrix}\) U183887 山区建小学期望版
容斥
-
本质
\(\pi\)为\(a\)所有可能取值的集合,\(p_i\)为\(a_i\)所有可以取的值的集合,\(U=\{x\in\mathbb{Z}|1\leq x\leq n\}\)
\[\begin{aligned} \sum\limits_{a\in\pi}\prod\limits_{1\leq i\leq n}[a_i\in p_i]&=\sum\limits_{a\in\pi}\prod\limits_{1\leq i\leq n}(1-[a_i\in p_i])\\ &=\sum\limits_{a\in\pi}\sum\limits_{S\subseteq U}\prod\limits_{i\in S}[a_i\notin p_i](-1)^{|S|}\\ &=\sum\limits_{S\subseteq U}(-1)^{|S|}\sum\limits_{a\in\pi}\prod\limits_{i\in S}[a_i\notin p_i] \end{aligned} \] -
min-max容斥
\[\max(S)=\sum_{T\subseteq S}(-1)^{|T|+1}\min(T) \]- 证明:
\[\begin{aligned} \max(S)&=\sum_{i\in S}a_i\prod_{j\in S,j\neq a_i}[a_i>a_j]\\ &=\sum_{i\in S}a_i\prod_{j\in S,j\neq a_i}(1-[a_i\leq a_j])\\ &=\sum_{i\in S}a_i\sum_{T\subseteq S,i\in T}(-1)^{|T|+1}\prod_{j\in T}[a_i\leq a_j]\\ &=\sum_{T\subseteq S}(-1)^{|T|+1}\sum_{i\in T}a_i\prod_{j\in T}[a_i\leq a_j]\\ &=\sum_{T\subseteq S}(-1)^{|T|+1}\min(T) \end{aligned}\]- 期望线性性:
\[E(\max(S))=\sum_{T\subseteq S}(-1)^{|T|+1}E(\min(T)) \] -
选一个排列=1~n每个数都选=没有不选的数(虽然是废话,但是做容斥的时候可能有用)
-
\(m\)个相同的球放进\(n\)个不同的盒子,但是每个盒子有上限:容斥,枚举一个集合超过上限
概率
-
若对于每个状态,有一个合法转移集合\(S_1\),每次随机选取合法转移集合中的一个状态转移
对每个状态构造另一个集合\(S_2\)满足\(S_1\subseteq S_2\),上述操作等价于每次从\(S_2\)中随机选取一个元素,若不合法再重选(重选时可以指定新的集合\(S_3\)满足\(S_1\subseteq S_3\))
- 用六面骰子造出\(1/5\)的概率——每次骰到一个数,如果是1~5的数就直接取,如果是6就再骰一遍
- [ARC114E] Paper Cutting 2 随机一个操作排列,若切到外面就跳过,若切到矩形就停止,每条线的贡献为它排在所有令它不合法的线前面的概率
- P5644 [PKUWC2018]猎人杀 死了不能再杀\(\to\)死了还能继续杀
- [USACO21DEC]T3 反着来,随机一个排列,若不合法则跳过\(\to\)每次在合法区间里随机选一个
-
搞清楚是事先做出所有决策还是决策可以动态调整
-
期望线性性:对于任意两变量\(X,Y\)(不要求独立),有\(E(X+Y)=E(X)+E(Y)\)
-
期望状态倒着设,因为不知道从各入边到达的概率,但知道从各出边出发的概率
排列
- 每个排列都是由若干个置换环组成的
- 考虑dp第i个位置有多少向后的箭头
- DP的时候考虑从小往大或从大往小插入每个元素 P2401 不等数列
- DP记录当前的值在剩下可取数中的排名 P2467 [SDOI2010]地精部落
序列DP
-
单调栈、单调队列、斜率优化、决策单调性,总之各种单调都要注意利用
-
如果将序列分成2部分,\(f_{i,0/1}\)表示决策完前\(i\)个,且第\(i\)个分到了\(0/1\)类,且\(i\)是当前一段的结尾,\(i+1\)和\(i\)不一样,这样枚举上一个点的时候就方便判断是否合法CF1144G Two Merged Sequences,AT2292 [AGC009C] Division into Two
-
\(f_i=\min\{\max(g(j),w(j,i))\}\),\(w(j,i)\)随\(j\)单调递增,随\(i\)单调递增
显然转移点应该在\(g\)的单调栈上,每次转移点只用找\(g\)的单调栈和\(w\)两函数相交的点,用一个指针维护转移点[蓝桥杯2021A]分果果 P1973 [NOI2011] NOI 嘉年华
![]()
-
括号序列区间DP:枚举\(l\)左括号所匹配的右括号 P7914 [CSP-S 2021] 括号序列
-
一个一个消数:考虑一个区间最后一个消掉的数 U188373 比赛
-
区间消消乐 \(f_{val,l,r}\)表示目前正在消\([l,r]\),且\(l\)前面还跟着一段(包含\(l\)),其权值为\(val\),转移就是消掉\(l\)前面这一段或者枚举下一个和\(l\)一起消的元素
\[f_{val,l,r}=\max\left\{f_{w[l+1],l+1,r}+val,\max\limits_{l<k\leq r}\left\{f_{merge(val,w[k]),k,r}+f_{w[l+1],l+1,k-1}\right\}\right\} \] -
区间最值可以考虑笛卡尔树,区间最值就是两端点在笛卡尔树上的LCA,转化为树上问题CF1580D Subsequence
-
如果dp数组值域特别小,可以考虑把dp值计入状态,把原来的状态变成新的dp值 CF1342F Make It Ascending
-
延迟决策,遍历到某个点的时候,可以把它先晾着,到后面再决策
状压DP
-
\(3^n\)枚举子集(问保安)
for (int s = 0; s < (1 << n); s++){ for (int s1 = s; ; s1 = (s1 - 1) & s){ //... if (!s1) break; } } -
\(f_{s1,s2}\)表示上一个数前\(n/2\)位为\(s1\),这一个数后\(n/2\)位为\(s2\)时的贡献 P3773 [CTSC2017]吉夫特,[CSP-S2020初赛] 第 20 题
-
状压DP多记录一些中间状态帮助转移
- P3921 小学数学题 多记录一维\(j\)表示当前集合前\(j\)位已经决策完成
- U86022 瘟疫公司(plague) 记录当前的集合的大小就行,剩下一维记录可以转移的集合
-
强连通分量容斥:统计不合法的情况,枚举当前点集中拓扑序最小的强连通分量,这个强联通分量向点集中其他点都连出边 CF1556F Sports Betting
-
无向连通图容斥:枚举集合中某个特定点所在的连通块
令\(f_{S,i}\)为在集合\(S\)的生成子图中选\(i\)条边联通的方案数
\[\forall u\in S, f_{S,i}=\begin{pmatrix}cnt(S)\\i\end{pmatrix}-\sum\limits_{u\in T,T\subsetneq S}\sum\limits_{j\leq i}f_{T,j}\begin{pmatrix}cnt(S-T)\\i-j\end{pmatrix} \]
树
-
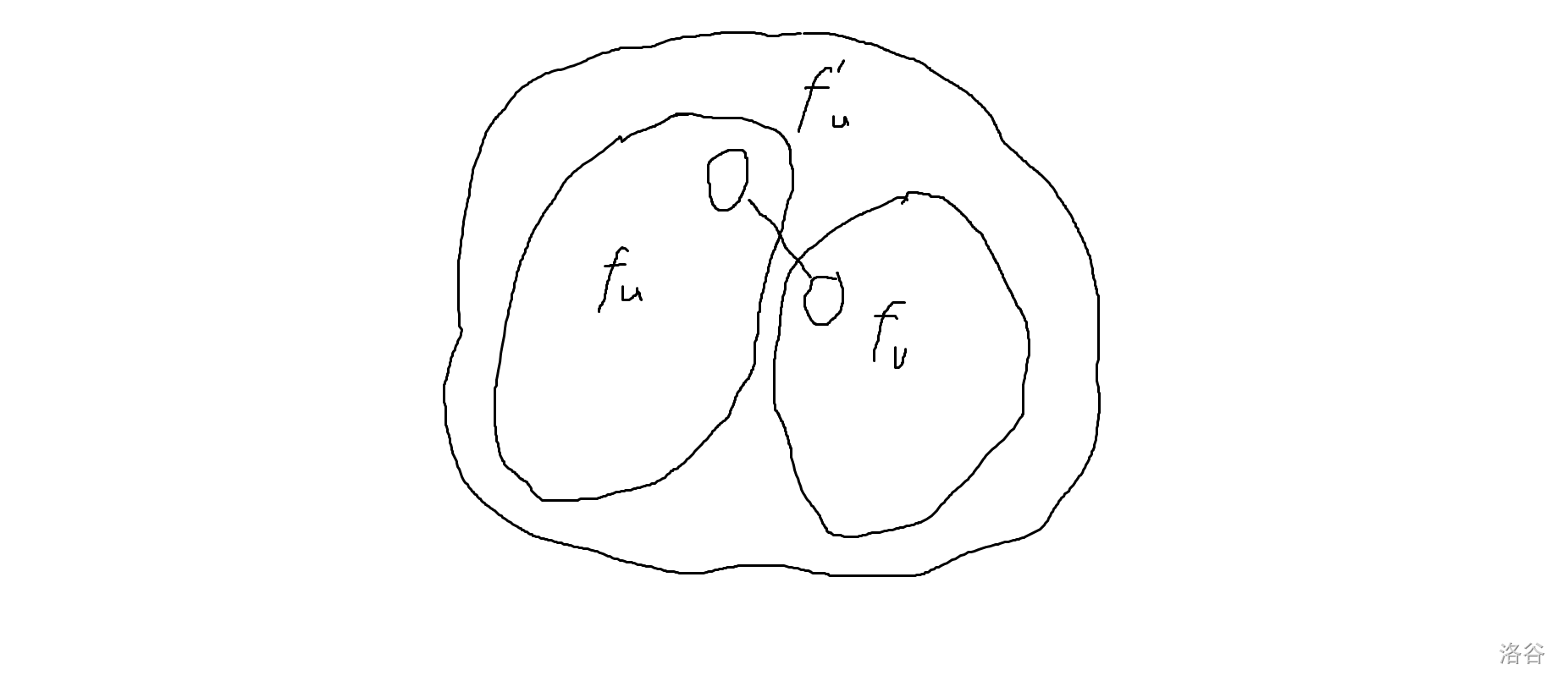
转移\(f'_u=\operatorname{merge}(f_u,f_v)\)
![]()
-
子树DP\(f\),裤衩DP\(g\)
![]()
-
子树合并:若每个节点\(u\)合并子树\(v\)时的复杂度为\(O(sz_u\cdot sz_v)\),则总复杂度为\(O(n^2)\)
-
虚树上边权和:所有点按照dfn排序,相邻两个点的路径和再加上第一个点和最后一个点的路径和 P5840 [COCI2015]Divljak
-
入栈序(\(dfn\))、出栈序(\(T\))
- \(v\)在\(u\)子树中:\(dfn_u\leq dfn_v\leq dfn_u+sz_u-1\)
- \(v\)在\(u\)至根的路径中:\(dfn_u\leq dfn_w\)且\(T_u\geq T_w\) P2305 [NOI2014] 购票
-
直径:从任意一点开始DFS,找到距离最远的点即为直径的一个端点,再从这个端点DFS找到距离最远的点,就是直径的另一个端点
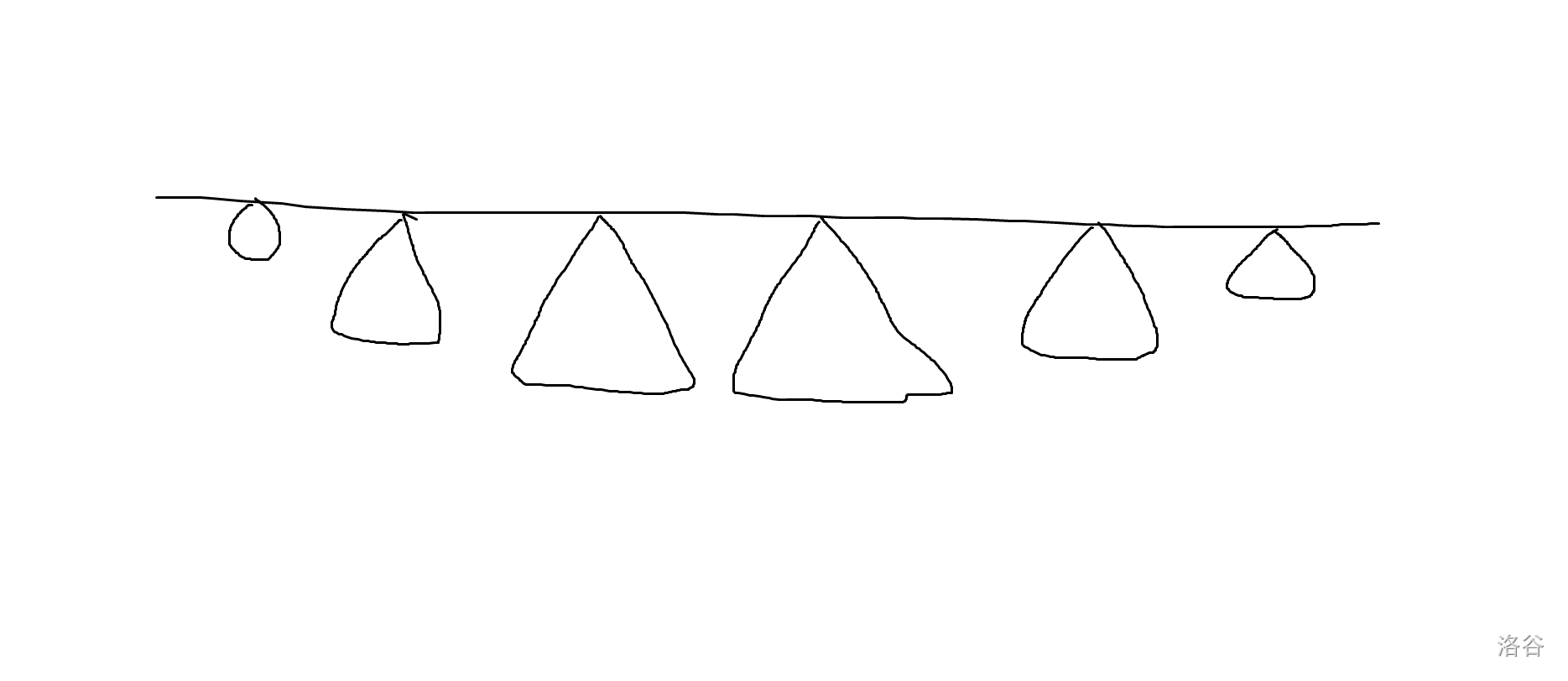
-
多想一想这张图,每棵子树的深度都小于顶点和直径端点的距离P2491 [SDOI2011]消防
![]()
-
树的重心\(\Leftrightarrow\)所有子树大小小于一半\(\Leftrightarrow\)和所有点的距离和最小
-
一棵树的重心在这棵树以任意点为根的重链上 P5666 [CSP-S2019] 树的重心
-
修改一个点(路径)附近点的权值:父亲和重儿子暴力改,其他儿子打tag,查询时直接看链顶父亲的tag CF487E Tourists P7735 [NOI2021] 轻重边
-
\(V-E\)容斥,统计所有点的贡献,再减去所有边的贡献,就是所有连通块的贡献
对于树上一个联通子图\(S\),有\([S\neq\phi]=\sum\limits_{v\in S}1-\sum\limits_{e\in S}1\)
- P5291 [十二省联考 2019] 希望 令连通块\(S\)内满足条件的点所构成的子图为\(T(S)\),答案可表示为
\[ \begin{aligned} ans&=\sum_{S_1,S_2,\cdots,S_k}[T(S_1\cap S_2\cap\cdots\cap S_k)\neq\phi]\\ &=\sum_{S_1,S_2,\cdots,S_k}(\sum_{v\in T(S)}1-\sum_{e\in T(S)}1)\quad S=S_1\cap S_2\cap\cdots\cap S_k\\ &=\sum_v f(v)^k-\sum_e g(e)^k\quad f(v)=\sum_{v\in T(S)} 1,g(e)=\sum_{e\in T(S)} 1 \end{aligned} \]\[ \begin{aligned} ans_i&=\sum_{c_1,c_2,\cdots,c_i}[T\neq\phi]\quad T=\bigcap_{j=1}^iS_{c_j}\\ &=\sum_{c_1,c_2,\cdots,c_i}(\sum_{v\in T}1-\sum_{e\in T}1)\\ &=\sum_v\begin{pmatrix}f(v)\\i\end{pmatrix}-\sum_e\begin{pmatrix}g(e)\\i\end{pmatrix}\quad f(v)=\sum_j[v\in S_j],g(e)=\sum_j[e\in S_j]\end{aligned} \] -
点分树优化DP:用点分树将\(dis(u,v)\)拆成\(dep[u]+dep[v]\) [牛客挑战赛54] F-小葱的树
-
点分治接单调队列,按照分治中心每个子树的高度排序,这样单调队列预处理复杂度就一定小于当前子树大小 P4292 [WC2010]重建计划
-
对于树上边集的一个子集,\(u\)和\(v\)在一个连通块中等价于\(v\)和最靠上能到达\(u\)的点分治中心在同一连通块
-
关于\(dep(LCA(u,v))\):可以考虑修改\(u\)到祖先的链,查询\(v\)到祖先的链 P5305 [GXOI/GZOI2019]旧词,P4211 [LNOI2014]LCA
-
树上两路径是否点相交:若点相交,其中一条路径的LCA一定在另一条路径上
-
树上两路径是否边相交:
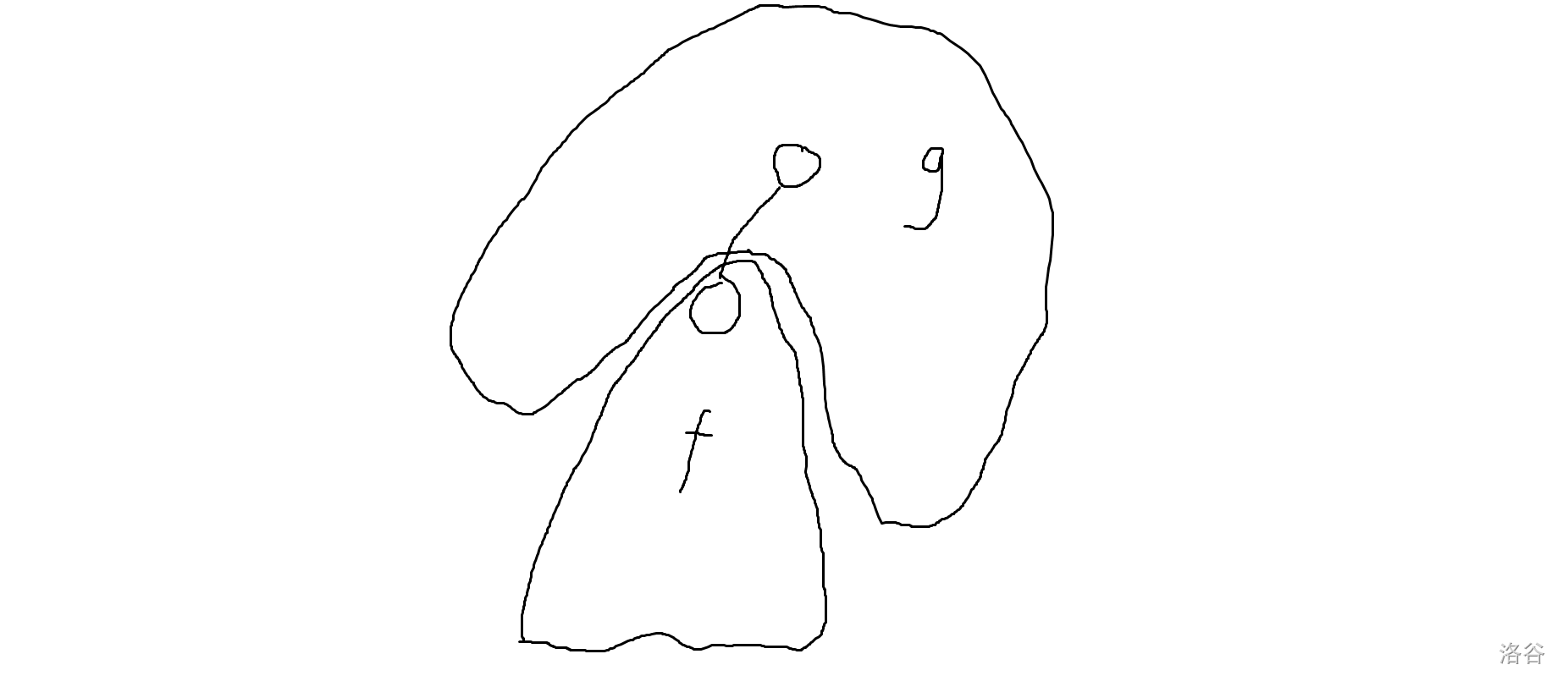
![]()
如图,若\(dis(u_1,u_2)+dis(v_1,v_2)=dis(u_1,v_2)+dis(v_1,u_2)\)则无边相交否则边相交,且交出的链长度为\(\frac 12|dis(u_1,u_2)+dis(v_1,v_2)-dis(u_1,v_2)-dis(v_1,u_2)|\)
-
树上两点集交的直径\(d(S_1\cup S_2)\subseteq d(S_1)\cup d(S_2)\)其中\(d(S)\)表示点集\(S\)直径的两端点,两个点集交的直径两端点一定是原两集合的端点\(\binom{4}{2}\)种组合其中之一
P4775 [NOI2018] 情报中心 -
dfs序背包:在dfs到\(u\)时,\(f_v\)表示只考虑dfs序上在\(u\)前的点时\(v\)子树对应的dp值 T261510 和谐社会(harmony)
-
树上相邻交换: AT3957 [AGC023F] 01 on Tree
-
“连通块大小乘积之和”:两个dp数组\(f,g\) 博物馆记忆之树(memory)
- \(f_u\)代表在\(u\)子树内所有联通块大小乘积之和
- \(g_u\)代表在\(u\)子树内不包括\(u\)所在联通块的所有联通块大小乘积之和
- 递推
- 相连:\(f'_u=f_u\cdot g_v+f_v\cdot g_u\),\(g'_u=g_u\cdot g_v\)
- 不相连:\(f'_u=f_u\cdot f_v\),\(g'_u=g_u\cdot f_v\)
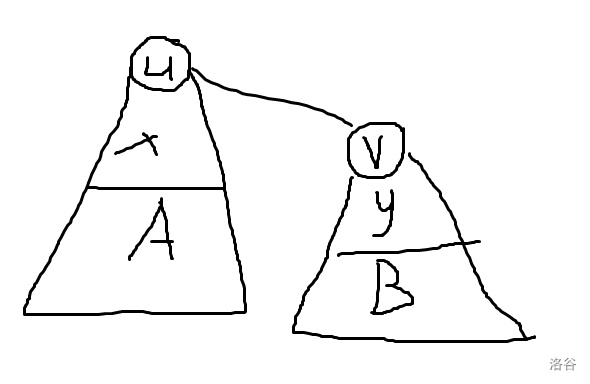
![]()
- 如图\(A(x+y)B=(Ax)B+A(yB)\)
图论
-
有向图的边可以分类成:树边、前向边、返祖边、横叉边
-
无向图的边可以分类成:树边、前向边(返祖边)
-
一个点到其他点的所有最短路径组成一个DAG
-
差分约束:如果同时存在\(x_i+x_j\leq d\)和\(x_i-x_j\leq d\)两种限制,将所有\(x\)按照\(x_i+x_j\leq d\)的边黑白染色,若染黑则差分约束时记录其负值,染白则记录正值 P7515 [省选联考 2021 A 卷] 矩阵游戏
-
线段树优化建图、倍增优化建图、ST表优化建图、前缀和优化建图:字面意思 CF786B Legacy
-
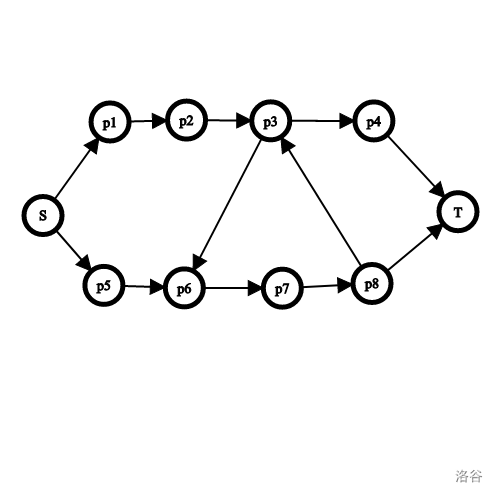
\(O(n^2)\)支配树:
- 枚举每个点,从根节点不经过这个点DFS,求出这个点支配的点集
- 类似拓扑排序,每一轮选择一个点当且仅当所有支配它的点已经遍历过了
-
圆方树:无向图,有诸如删点后是否可达的叙述,可以考虑在圆方树上搞
-
两点在圆方树路径上的圆点是这两个点在原图中路径的必经点 P5058 [ZJOI2004]嗅探器 P4082 [USACO17DEC]Push a Box P
-
两点在圆方树路径上所有方点的相邻点是这两点所有简单路径可能经过的点 P4630 [APIO2018] Duathlon 铁人两项
-
矩阵树定理可以求
\[\sum_{T\text{是生成树}}\prod_{e\in T}w_e \]一般取\(w_i=1\),必要时可以令\(w\)为一个多项式
令\(w=ax+b\),乘法为\(\bmod x^2\)意义下的乘法,可以求出所有生成树的权值和 P6624 [省选联考 2020 A 卷] 作业题
计数
-
容斥
-
第一次到达状态\(S\)的方案:到达\(S\)的方案减去之前到过但又回来的方案数 U105245 随机游走3 P8208 [THUPC2022 初赛] 骰子旅行
-
本质不同子序列个数:\(f_i=2f_{i-1}-f_{pre[i]-1}\),其中\(f_i\)表示前\(i\)个元素的不同子序列个数
钦定相同的子序列选取最后一个计数,每次决定第\(i\)个选不选,并且排除上一个选了和\(i\)同色的元素却没选\(i\)的情况,因为这样就会使统计的子序列不是最后一个,因为\(f_{i-1}\)满足所统计的子序列在前\(i-1\)中是最后一个,所以只可能是选了\(pre[i]\)没选\(i\)
选\(i\)的方案数:\(f_{i-1}\),不选\(i\)的方案数:\(f_{i-1}-f_{pre[i]-1}\)
-
-
不同维度间相互独立(但是可能没有完全独立) P5289[十二省联考 2019]皮配
-
统计贡献的思想非常重要,考虑每个元素对答案所做出的贡献
-
如果要计数若干个相似问题的和,且问题可以用若干线性变换解决,可以考虑将初始向量直接相加,再做一遍原问题 CF1810G The Maximum Prefix P3352 [ZJOI2016]线段树
\(\sum_i(\vec{v_i}\times A)=(\sum_i\vec{v_i})\times A\)
字符串
- 一个长\(n\)的字符串的所有border可以分成\(\log n\)个等差数列
矩阵乘法
-
不满足交换律,注意乘法顺序
-
广义矩阵乘法需要满足的条件
定义广义矩乘为
\[(A\times B)_{i,j}=\bigoplus\limits_{k=1}^{m}A_{i,k}\otimes B_{k,j} \]则其结合律、分配率依赖于
\[\begin{cases} (a\oplus b)\otimes c=a\otimes c\oplus b\otimes c\\ a\otimes(b\oplus c)=a\otimes b\oplus a\otimes c\\ a\oplus b=b\oplus a\\ (a\oplus b)\oplus c=a\oplus(b\oplus c) \end{cases} \]也就是\(\otimes\)和\(\oplus\)之间的分配率、\(\oplus\)的交换律和结合律
常见广义矩乘
- \(a\oplus b=\min(a,b),a\otimes b=a+b\) P2886 [USACO07NOV]Cow Relays G
- \(a\oplus b=a\operatorname{xor}b,a\otimes b=a\operatorname{and} b\) P6569 [NOI Online #3 提高组] 魔法值
- \((a\oplus b)_{i,j}=a_{i,j}+b_{i,j},(a\otimes b)_{i,j}=\sum_{k=1}^ma_{i,k}\cdot b_{k,j}\)(矩阵每个元素都是一个子矩阵)P6772 [NOI2020] 美食家 P5319 [BJOI2019]奥术神杖
动态DP(DDP)
- 将DP的式子改成一个向量乘上一堆矩阵的形式,用数据结构维护 CF1609E William The Oblivious
- 树上DDP:\(\vec{f}(u)=\vec{f}(hs(u))\times F_u\),其中\(F_u\)只与\(u\)的所有轻儿子有关 P4719 【模板】"动态 DP"&动态树分治
根号
- 根号分治
- 对于\(q\)个二元询问\((u,v)\),若满足\((u,v)\)的答案等于\((v,u)\)的答案,对于每个\(u\),可以经过\(f(u)\)时间预处理后以\(g(v)\)时间回答询问\((u,v)\),则可以在\(O(\sqrt q\sum_ig(i)+\sum_if(i))\)时间回答所有询问 共同好友乱搞解法
网络流
-
限制点的流量:拆点,两点间连边的限制为点流量限制
-
DAG最小路径覆盖:拆点,每个点的流量下限为1,跑有上下界最小流
-
有若干形如\(a[b_1]+a[b_2]+\cdots+a[b_k]\in[L_i,R_i]\)的限制,限制可分为两组,每个\(a[i]\)在同一组中只出现一次,且每个\(a[i]\)取值范围在\([l_i,r_i]\)
- 每个\(a[i]\)建两个点,中间的边按照它的取值范围设定上下界
- 对于第一组中的限制,建点,从源点到这个点连一条\([L_i,R_i]\)的边,从这个点向所有受限制的点连一条容量无限的边
- 对于第二组中的限制,建点,从这个点到汇点连一条\([L_i,R_i]\)的边,从每个受限制的点连到这个点一条容量无限的边
- P4486 [BJWC2018]Kakuro
-
二分图相关:
- 最小点覆盖=最大匹配(最小割)
- 最小边覆盖=N-最大匹配(除了匹配,每条边覆盖一个点)
- 最大独立集=N-最大匹配(除了最小点覆盖的点)
-
最大权闭合子图:有\(n\)个点,有\(m\)个限制\((u,v)\)表示取点\(u\)就一定要取点\(v\),每个点有一个权值\(w_i\)(可正可负),求一个满足限制的选点方案使选点权值和最大
- 对每个限制\((u,v)\),连一条\((u,v,\infin)\)的边,对每个\(w_i\geq 0\)的点,先给答案加上\(w_i\),再连边\((S,i,w_i)\),若\(w_i<0\),则连边\((i,T,|w_i|)\),最后答案减去最大流
- 证明(感性):最小割
- CF1146G Zoning Restrictions
- 正权点同时连向若干个点等价于这些点全选时权值增加
- 对于两个点,通过上述方法拼上改变两点本身的权值,可以实现:
u\v 0 1 0 + - 1 - + - P8215 [THUPC2022 初赛] 分组作业
-
切糕模型
- upd:切糕模型可以转化为最大权闭合子图
- \((u,v)\to(u,v-1)\)
- 限制\(x\ge y+k\):\((y,i)\to (x,i+k)\)
- 钦定选\((u,1)\):\(S\to (u,1)\)(dfs删点常数会更优一些)
- \(w'(u,v)=w(u,v)-w(u,v-1)\)
- 以下是经典做法:
![]() (盗题解图)
(盗题解图)- 对于每个变量,每种取值都开一个点
- 连边:
- \(S\to (x,1),flow=\infin\)
- \((x,lim+1)\to T,flow=\infin\)
- \((x,i)\to (x,i+1),flow=weight(x,i)\)
- \((x,i+1)\to (x,i),flow=\infin\)
- \(\forall u\geq v+k,(v,i)\to (u,i+k),flow=\infin\)
- 做最小割,显然每个变量\(S\)只可达一个前缀,只割一条边,若割\((x,i)\to(x,i+1)\),则代表\(x\)取值为\(i\)
- P3227 [HNOI2013]切糕
- upd:切糕模型可以转化为最大权闭合子图
-
平面图最小割转最短路:(如果原图是有向图,对偶图中的边只能全是从原图一条边的左边到右边或全是从右边到左边)P4001 [ICPC-Beijing 2006]狼抓兔子
其他
-
所求答案数组单调且值域不大,二分每一个相同段的长度
- CF1039D You Are Given a Tree 可以\(O(n)\)求出一个答案,根号分治,长度大于\(B\)的答案不超过\(n/B\),二分每一段的长度,取\(B=\sqrt{n\log n}\),总复杂度为\(O(n\sqrt{n\log n})\)
-
\(x=p_1^{a_1}\times p_2^{a_2}\cdots\times p_k^{a_k}\),可以将每个质因子视作一维,将\(x\)视作一个高维的点,坐标为\((a_1,a_2,\cdots,a_k)\) U184638 仪式感 (sor),P8255 [NOI Online 2022 入门组] 数学游戏
-
高维前缀和:枚举每一维,做这一维的前缀和
可以处理子集权值和,约数权值和
二维的例子:
for (int i = 1; i <= n; i++){ for (int j = 1; j <= m; j++){ a[i][j] += a[i - 1][j]; } } for (int i = 1; i <= n; i++){ for (int j = 1; j <= m; j++){ a[i][j] += a[i][j - 1]; } } -
\(a[1...n]\)中\(a_i\|a_j\)最大值:对每个\(a_i\),取其补集\(U-a_i\),从大到小枚举补集的每一位,如果有元素为当前已选集合的超集的话就选
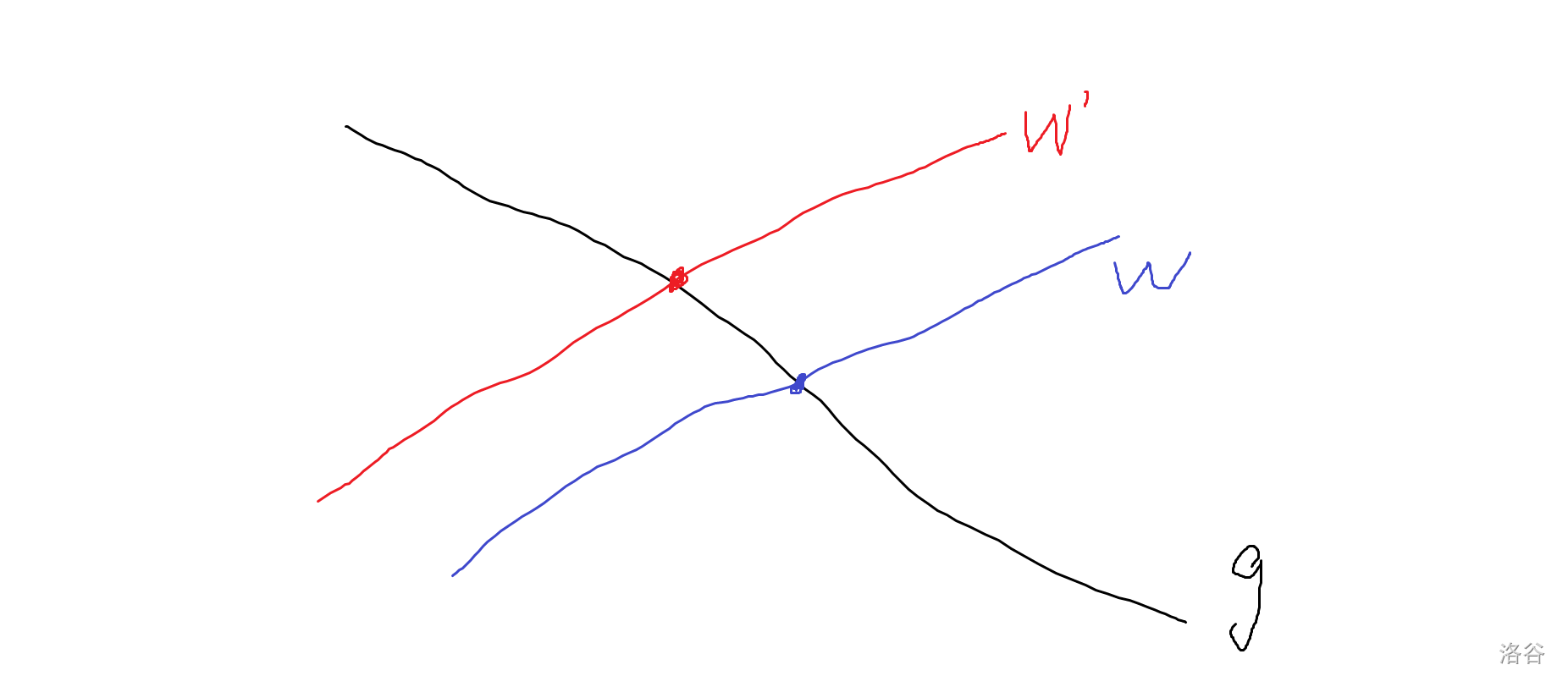

 (盗题解图)
(盗题解图)
 浙公网安备 33010602011771号
浙公网安备 33010602011771号