268.和算法执行时间相关的因素
1.决定因素
1.1算法选用的策略
1.2问题的规模
1.3编写程序的语言
1.4编译程序产生的机器代码的质量
1.5计算机执行指令的速度
2.其他影响元素
3.问题的规模（时间复杂度）
3.1定义
一个特定算法的“运行工作量”的大小，只依赖于问题的规模（通常用整数量n表示），或者说，它是问题规模的函数。
假如，随着问题规模 n 的增长，算法执行时间的增长率和 f(n) 的增长率相同，则可记作：T (n) = O(f(n)), 称T (n) 为算法的(渐近)时间复杂度。
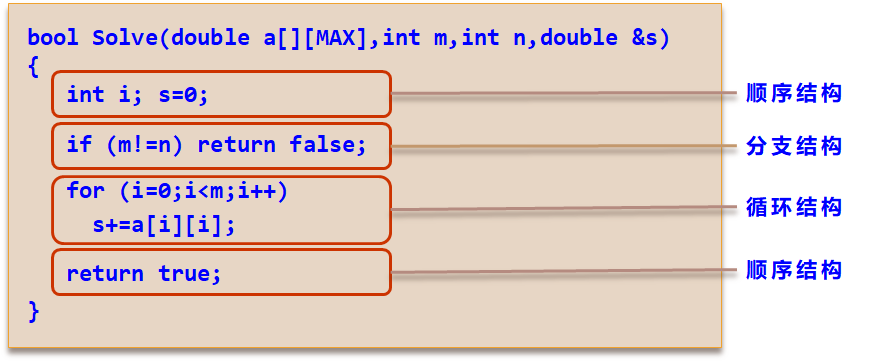
一个算法是由控制结构（顺序、分支和循环3种）和原操作（指固有数据类型的操作）构成的，算法的运行时间取决于两者的综合效果。
3.2估算算法的时间复杂度
（Time Complexity）
3.2.1定义
从算法中选取一种对于所研究的问题来说是基本操作的原操作，以该基本操作 在算法中重复执行的次数 作为算法运行时间的衡量准则。
“基本操作” 指的是，该操作重复执行次数和算法的运行时间成正比。
算法的执行时间=∑原操作(i)的执行次数×原操作(i)的执行时间
详细算法的执行时间与原操作执行次数之和成正比
算法= 控制结构+ 原操作（固有数据类型的操作）
1两个矩阵相乘 eg1:两个矩阵相乘 void mult(inta[], int b[], int&c[] ) { // 以二维数组存储矩阵元素，c为 a 和 b的乘积 for (i=1; i<=n; ++i){ for(j=1; j<=n; ++j) { c[i,j] = 0; for(k=1; k<=n; ++k) c[i,j] += a[i,k]*b[k,j]; } } } 基本操作: 乘法操作时间复杂度: O(n^3)
2选择排序
3起泡排序
4有如下递归函数fact(n)，分析其时间复杂度 int fact(int n){ if(n<=1) return(1); (1) else return(n*fact(n-1)); (2） } 解：设fact(n)的运行时间复杂函数是T(n)， 该函数中语句(1)的运行时间是O(1), 语句(2)的运行时间为：T(n-1)+O(1), 其中O(1)为基本运算时间， 因此： T(n) = O(1)+T(n-1) = O(1)+O(1)+T(n-2) = …… = (n-1)*O(1)+T(1) = n*O(1) = O(n)则fact(n)的时间复杂度为O(n)。
3.2.2分析算法时间复杂度的一般步骤
3.2.3渐进符号
设n为算法中的问题规模，通常用大O、大Ω和Θ等三种渐进符号表示算法的执行时间与n之间的一种增长关系。
3.2.3.1 大O符号
定义
定义1（大O符号），f(n)=O(g(n))（读作“f(n)是g(n)的大O”）当且仅当存在正常量c和n0，使当n≥n0时，f(n)≤cg(n)，即g(n)为f(n)的上界。
如3n+2=O(n)，因为当n≥2时，3n+2≤4n。
10n2+4n+2=O(n4)，因为当n≥2时，10n2+4n+2≤10n4。
大O符号用来描述增长率的上界，表示f(n)的增长最多像g(n) 增长的那样快，也就是说，当输入规模为n时，算法消耗时间的最大值。这个上界的阶越低，结果就越有价值，所以，对于10n2+4n+2，O(n2)比O(n4) 有价值。
一个算法的时间用大O符号表示时，总是采用最有价值的g(n)表示，称之为“紧凑上界”或“紧确上界”。
一般地，如果
有
常用的几种时间复杂度的关系
说明：
1.在难以精确计算基本操作执行次数（或语句频度）的情况下，只需求出它关于n的增长率或阶即可2.一个算法的时间复杂度可以具体分为最好、最差（又称最坏）和平均三种情况讨论。
除特别说明外，正常均指最坏情况下的时间复杂度。
例子
1两个矩阵相乘
eg1:两个矩阵相乘
void mult(inta[], int b[], int&c[] ) {
// 以二维数组存储矩阵元素，c为 a 和 b的乘积
for (i=1; i<=n; ++i){
for(j=1; j<=n; ++j) {
c[i,j] = 0;
for(k=1; k<=n; ++k)
c[i,j] += a[i,k]*b[k,j];
}
}
} 基本操作: 乘法操作时间复杂度: O(n^3)
2选择排序
3起泡排序
4有如下递归函数fact(n)，分析其时间复杂度
int fact(int n){
if(n<=1) return(1); (1)
else return(n*fact(n-1)); (2）
}
解：设fact(n)的运行时间复杂函数是T(n)，
该函数中语句(1)的运行时间是O(1),
语句(2)的运行时间为：T(n-1)+O(1),
其中O(1)为基本运算时间，
因此： T(n) = O(1)+T(n-1)
= O(1)+O(1)+T(n-2)
= ……
= (n-1)*O(1)+T(1)
= n*O(1)
= O(n)则fact(n)的时间复杂度为O(n)。
3.2.3.2 大Ω符号
定义2（大Ω符号），f(n)= Ω(g(n))（读作“f(n)是g(n)的大Ω”）当且仅当存在正常量c和nθ，使当n≥n0时，f(n)≥cg(n)，即g(n)为f(n)的下界。
如3n+2=Ω(n)，因为当n≥1时，3n+2≥3n。
10n2+4n+2=Ω(n2)，因为当n≥1时，10n2+4n+2≥n2。
大Ω符号用来描述增长率的下界，表示f(n)的增长最少像g(n) 增长的那样快，也就是说，当输入规模为n时，算法消耗时间的最小值。
与大O符号对称，这个下界的阶越高，结果就越有价值，所以，对于10n2+4n+2，Ω(n2)比Ω(n) 有价值。一个算法的时间用大Ω符号表示时，总是采用最有价值的g(n)表示，称之为“紧凑下界”或“紧确下界”。
一般地，如果
，有
。
3.2.3.3大Θ符号
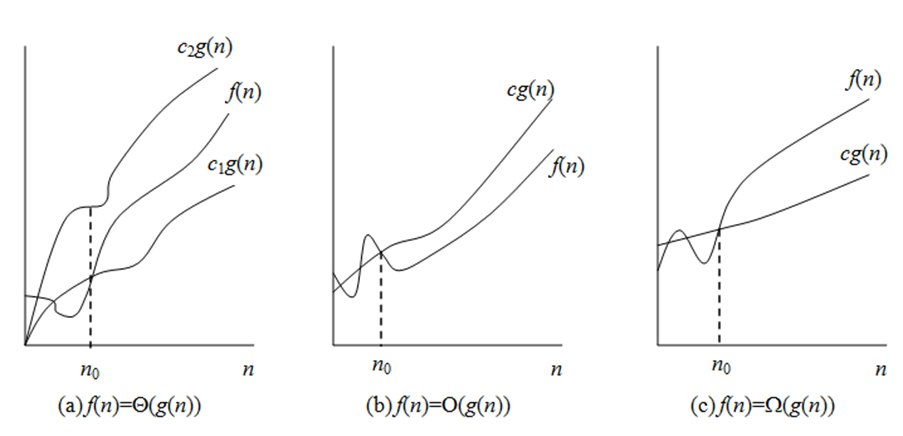
定义3（大Θ符号），f(n)= Θ(g(n))（读作“f(n)是g(n)的大Θ”）当且仅当存在正常量c1、c2和n0，使当n≥n0时，有c1g(n)≤f(n)≤c2g(n)，即g(n)与f(n)的同阶。
如3n+2=Θ (n)，10n2+4n+2=Θ(n2)。
一般地，如果
，有f(n)=Θ(nm)。
大Θ符号比大O符号和大Ω符号都精确，f(n)=Θ(g(n)，当且仅当g(n)既是f(n)的上界又是f(n)的下界。
3.2.3.4关系
3.3算法的最好、最坏和平均情况
设一个算法的输入规模为n，Dn是所有输入的集合，任一输入I∈Dn，P(I)是I出现的概率，有ΣP(I) =1，T(I)是算法在输入I下所执行的基本语句次数，则该算法的平均执行时间为：A(n)=
。
也就是说算法的平均情况是指用各种特定输入下的基本语句执行次数的带权平均值。
算法的最好情况为：G(n)=
，是指算法在所有输入I下所执行基本语句的最少次数。
算法的最坏情况为：W(n)=
，是指算法在所有输入I下所执行基本语句的最大次数。
4.算法选用的策略
4.3非递归算法的时间复杂度分析
对于非递归算法，分析其时间复杂度相对比较简单，关键是求出代表算法执行时间的表达式。
通常是算法中基本语句的执行次数，是一个关于问题规模n的表达式，然后用渐进符号来表示这个表达式即得到算法的时间复杂度。
【例1.6】给出以下算法的时间复杂度。 void func(int n) { int i=1,k=100; while (i<=n) { k++; i+=2; } } 解：算法中基本语句是while循环内的语句。
设while循环语句执行的次数为m，i从1开始递增，最后取值为1+2m，有： i=1+2m≤n f(n)=m≤(n-1)/2=O(n)。 该算法的时间复杂度为O(n)。
4.2递归算法的时间复杂度分析
递归算法是采用一种分而治之的方法，把一个“大问题”分解为若干个相似的“小问题”来求解。
对递归算法时间复杂度的分析，关键是根据递归过程建立递推关系式，然后求解这个递推关系式，得到一个表示算法执行时间的表达式，最后用渐进符号来表示这个表达式即得到算法的时间复杂度。
【例1.7】有以下递归算法： void mergesort(int a[],int i,int j) { int m; if (i!=j) { m=(i+j)/2; mergesort(a,i,m); mergesort(a,m+1,j); merge(a,i,j,m); } } 其中，mergesort()用于数组a[0..n-1]（设n=2k，这里的k为正整数）的归并排序，
调用该算法的方式为： mergesort(a，0，n-1)； 另外merge(a，i，j，m)用于两个有序子序列a[i..j]和a[j+1..m]的有序合并，
是非递归函数，它的时间复杂度为O(n)（这里n=j-i+1）。分析上述调用的时间复杂度。
解：设调用mergesort(a，0，n-1)的执行时间为T(n)，
由其执行过程得到以下求执行时间的递归关系（递推关系式）：
T(n)=O(1) 当n=1
T(n)=2T(n/2)+O(n) 当n>1
其中，O(n)为merge()所需的时间，设为cn（c为正常量）。因此：
T(n) = 2T(n/2)+cn=2[2T(n/22)+cn/2]+cn=22T(n/22)+2cn
= 23T(n/23)+3cn
= …
= 2kT(n/2k)+kcn
= nO(1)+cnlog2n=n+cnlog2n //这里假设n=2k，则k=log2n
= O(nlog2n)
【例1.8】求解梵塔问题的递归算法如下，分析其时间复杂度。 void Hanoi(int n,char x,char y,char z) { if (n==1) printf("将盘片%d从%c搬到%c\n",n,x,z); else { Hanoi(n-1,x,z,y); printf("将盘片%d从%c搬到%c\n",n,x,z); Hanoi(n-1,y,x,z); } }
解：设调用Hanoi(n，x，y，z)的执行时间为T(n)，由其执行过程得到以下求执行时间的递归关系（递推关系式）：
T(n)=O(1) 当n=1
T(n)=2T(n-1)+1 当n>1
T(n) = 2[2T(n-2)+1]+1=22T(n-2)+1+21
= 23T(n-3)+1+21+22
= …
= 2n-1T(1)+1+21+22+…+2n-2
= 2n-1 = O(2n)
