ACM预备队-大一下学期week(3)集训

1.饿饿，饭饭2

题目链接：饿饿 饭饭2 - Problem - Daimayuan Online Judge

#include <iostream>
using namespace std;

int main() {
    int T;
    cin >> T;
    while (T--) {
        int n;
        cin >> n;
        int a[n];
        for (int i = 0; i < n; i++) {
            cin >> a[i];
        }
        bool flag = true;
        for (int i = 0; i < n; i++) {
            while (a[i] % 2 == 0) {
                a[i] /= 2;
            }
            while (a[i] % 3 == 0) {
                a[i] /= 3;
            }
            if (a[i] != a[0]) {
                flag = false;
                break;
            }
        }
        if (flag) {
            cout << "YES" << endl;
        } else {
            cout << "NO" << endl;
        }
    }
    return 0;
}

2.子串分值和

题目链接：子串分值和 - Problem - Daimayuan Online Judge

暴力会TLE，加上每一个元素的贡献值和O(N)的复杂度，算一下每一个字母对自己及后面的贡献值

 

#include <bits/stdc++.h>
using namespace std;
int pos[30];//类似于指针
//1e6的复杂度，所以只能O(n)所以计算每个字母对后面位置的 
inline void solve()
{
    string s;
    cin>>s;
    int len=s.size();//一定要提前存储字符串的长度，如果是后面添加了一个元素后取size，就得所有关于len的地方都得-1，注意不要越界！！！ 最好在加上一个0位置元素前取size 
    s="?"+s;
    long long res=0;
    for(int i=1;i<=len;i++)
    {
        res=res+(i-pos[s[i]-'a'])*(len-i+1);//因为所有的贡献和就是前面的不包含上一个s[i]字符后面开始到串末的可能性，乘法原理，其中第i个位置可以选也可以不选
        pos[s[i]-'a']=i;
    }
    cout<<res<<endl;
}
signed main()
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    solve();
    return 0;
}

 

3.蒟蒻

题目链接：蒟蒻 - Problem - Daimayuan Online Judge

#include <bits/stdc++.h>
using namespace std;
int n;
map<int,int>m1;//第一关键字：m1是价格，m2是口感 
map<int,int>m2;
signed main()
{
    scanf("%d",&n);
    while(n--)
    {
        int op,w,t;
        scanf("%d",&op);
        if(op==1) 
        {
            scanf("%d%d",&w,&t);
            if(m1.count(w)==0 && m2.count(t)==0)
            {
                m1[w]=t;
                m2[t]=w;
            }    
        }
        else if(op==2)
        {//必须先清除掉m2，要不先m1会数据丢失 
            m2.erase(m1.begin()->second);
            m1.erase(m1.begin());
        }
        else if(op==3)
        {//必须先清除m1,要不先m2的话m1清除的就错了 
            m1.erase(m2.begin()->second);
            m2.erase(m2.begin());

        }
    }    
    int res=0;
    for(auto x:m1)
    {
        res+=x.first;
    }
    printf("%d",res);
} 

4.锦标赛

题目链接：锦标赛 - Problem - Daimayuan Online Judge

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N];
long long res=1;
int n,k;
signed main()
{
     scanf("%d%d",&n,&k);
     for(int i=0;i<n;i++) scanf("%d",&a[i]);
     sort(a,a+n,greater<int>());
     for(int i=0;i<n-1;i++)
     {
         if(a[i]-a[i+1] <=k)res++;
         else break;
     }
     printf("%d",res);
}

5.可重排列

题目链接：可重排列 - Problem - Daimayuan Online Judge

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL sum,res;
int n;
const int N=10;
int a[N];
vector<int>v;
void dfs()
{
    if(v.size()==sum)
    {
        for(auto i:v)printf("%d ",i);
//        for(int i=0;i<v.size();i++) printf("%d ",v[i]);
        printf("\n");
        return;
    }
    for(int i=1;i<=n;i++)
    {
        if(a[i]!=0)
        {
            a[i]--;
            v.push_back(i);
            dfs();
            v.pop_back();
            a[i]++;
        }
    }
}
signed main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)scanf("%d",&a[i]),sum+=a[i];//此时a[i]存储的是1~n的数字总数 
    dfs();
    return 0;
}

6.掷骰子：

假设你有m个n面骰子（点数∈[1，n],求掷这m个骰子，点数和大于等于k的概率，结果 保留两位小数（可使用f'{num :.2%}'格式化输出，使num以百分数形式并保留2为小数 输出). 提示： 可以模拟该过程，先编写函数求出点数和等于某个值的概率，再进行累加.1≤m,n≤6 输入输出格式： 输入格式： 一行由空格隔开的三个数字，分别代表m,n,k 输出格式： 一行数字，表示概率。

 

题目样例：
输入：
1 6 6
输出：
16.67%
输入：
2 6 11
输出：
8.33%

 

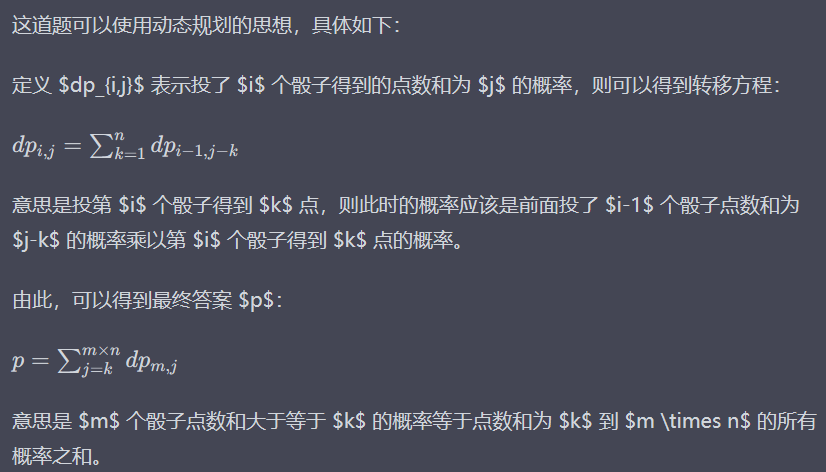
 注意：%%转移是百分号＋百分号，而大多数都是\转义

#include <bits/stdc++.h>
using namespace std;

int m, n, k;
double dp[7][42]; // 注意数组大小

int main() {
    cin >> m >> n >> k;

    // 初始化 dp 数组
    for (int j = 1; j <= n; j++) {
        dp[1][j] = 1.0 / n;
    }

    // 计算 dp 数组
    for (int i = 2; i <= m; i++) {
        for (int j = i; j <= m * n; j++) {
            for (int p = 1; p <= n; p++) {
                if (j - p > 0) {
                    dp[i][j] += dp[i - 1][j - p]/n;
                }
            }
        }
    }

    // 计算最终概率
    double p = 0;
    for (int j = k; j <= m * n; j++) {
        p += dp[m][j];
    }

    // 输出结果
    printf("%.2f%%\n", p * 100);

    return 0;
}

def dice_probability(n: int, sum: int) -> float:
    """
    求掷 n 个 6 面骰子，点数和等于 sum 的概率
    """
    if sum < n or sum > n * 6:
        return 0  # 和小于 n 或大于 6n，概率为 0
    dp = [0] * (sum + 1)
    dp[0] = 1
    for i in range(1, n + 1):
        for j in range(sum, i - 1, -1):
            dp[j] = 0
            for k in range(1, 7):
                if j - k >= i - 1:
                    dp[j] += dp[j - k] / 6
    return dp[sum]

m, n, k = map(int, input().split())
p = sum(dice_probability(m, i) for i in range(k, m * n + 1))
print(f'{p :.2%}')